Đề thi Cuối học kì 2 Toán 6 có đáp án (Đề 2)
-
3137 lượt thi
-
13 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D
Ta có: \(\frac{{ - 15}}{9} = \frac{{ - 15:3}}{{9:3}} = \frac{{ - 5}}{3} = \frac{{ - 5.9}}{{3.9}} = \frac{{ - 45}}{{27}}\)
Do đó \(\frac{{ - 15}}{9} = \frac{{ - 45}}{{27}}\)
Suy ra x = –45.
Vậy x = –45.
Câu 2:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C
Ta có: \(\frac{8}{{11}}\) của –5 tức là \(\frac{8}{{11}}.\left( { - 5} \right) = \frac{{8.\left( { - 5} \right)}}{{11}} = \frac{{ - 40}}{{11}}.\)
Vậy \(\frac{8}{{11}}\) của –5 là \( - \frac{{40}}{{11}}\).
Câu 3:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B
Ta có: –0,75 của a bằng 15 tức là –0,75.a = 15
Suy ra a = 15 : (–0,75)
a = –20.
Vậy a = –20.
Câu 4:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A
Tỉ số phần trăm số giấy vụn mà lớp 6A đã thu được so với khối 6 của trường là:
\(\frac{{105}}{{1035}}.100\% = 10,144\% \)
Làm tròn kết quả trên đến chữ số thập phân thứ nhất ta được kết quả là 10,1%.
Câu 5:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C
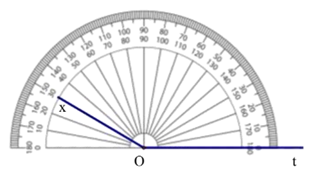
Nhìn thước đo góc ta có góc tOx có số đo là 150°.
Vì 150° > 90° nên góc tOx (hay góc xOt) là góc tù.
Câu 6:
Khi đó:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D
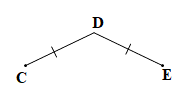
Điểm D không nằm trên đoạn thẳng EC nên điểm D không là trung điểm của đoạn thẳng EC.
Câu 7:

 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B
Ta quan sát biểu đồ cột thấy ba cột biểu thị nhiệt độ cao nhất trong năm là tháng 5, tháng 6 và tháng 7.
Câu 8:
Tung hai đồng xu cân đối một số lần ta được kết quả sau:
|
Sự kiện |
Hai đồng ngửa |
Hai đồng sấp |
Một đồng ngửa, một đồng sấp |
|
Số lần |
10 |
14 |
26 |
Xác suất thực nghiệm của sự kiện hai đồng xu đều sấp là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C
Tổng số lần thực hiện hoạt động tung hai đồng xu là: 10 + 26 + 14 = 50 (lần).
Số lần cả hai đồng xu đều sấp là 14 lần.
Xác suất thực nghiệm của sự kiện cả hai đồng xu đều sấp là: \(\frac{{14}}{{50}} = \frac{7}{{25}}\).
Câu 9:
PHẦN II. TỰ LUẬN (8 điểm)
Thực hiện phép tính (tính hợp lí nếu có thể):
a) 34,9 – 31,5 + 58,8 – 55,4
b) \[\frac{{ - 3}}{{31}} - \frac{6}{{17}} - \frac{{ - 1}}{{25}} + \frac{{ - 28}}{{31}} + \frac{{ - 11}}{{17}} - \frac{1}{5}\]
c) \[2\frac{2}{9}:1\frac{1}{9} - \frac{{46}}{5}:4\frac{3}{5}\]
d) \[\left( {4 - \frac{{12}}{{10}}} \right):2 + 30\% \]
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
a) 34,9 – 31,5 + 58,8 – 55,4
= (34,9 – 31,5) + (58,8 – 55,4)
= 3,4 + 3,4
= 6,8
b) \[\frac{{ - 3}}{{31}} - \frac{6}{{17}} - \frac{{ - 1}}{{25}} + \frac{{ - 28}}{{31}} + \frac{{ - 11}}{{17}} - \frac{1}{5}\]
\[ = \frac{{ - 3}}{{31}} + \frac{{ - 28}}{{31}} - \frac{6}{{17}} + \frac{{ - 11}}{{17}} - \frac{{ - 1}}{{25}} - \frac{1}{5}\]
\[ = \left( {\frac{{ - 3}}{{31}} + \frac{{ - 28}}{{31}}} \right) + \left( { - \frac{6}{{17}} + \frac{{ - 11}}{{17}}} \right) + \left( { - \frac{{ - 1}}{{25}} - \frac{1}{5}} \right)\]
\[ = \frac{{\left( { - 3} \right) + \left( { - 28} \right)}}{{31}} + \frac{{\left( { - 6} \right) + \left( { - 11} \right)}}{{17}} + \left( {\frac{1}{{25}} - \frac{5}{{25}}} \right)\]
\[ = \frac{{ - 31}}{{31}} + \frac{{ - 17}}{{17}} + \frac{{1 - 5}}{{25}}\]
\( = \left( { - 1} \right) + \left( { - 1} \right) + \frac{{ - 4}}{{25}}\)
\( = - 2 + \frac{{ - 4}}{{25}}\)
\( = \frac{{ - 50}}{{25}} + \frac{{ - 4}}{{25}}\)
\( = \frac{{ - 50 + \left( { - 4} \right)}}{{25}}\)
\( = \frac{{ - 54}}{{25}}.\)
c) \[2\frac{2}{9}:1\frac{1}{9} - \frac{{46}}{5}:4\frac{3}{5}\]
\[ = \frac{{20}}{9}:\frac{{10}}{9} - \frac{{46}}{5}:\frac{{23}}{5}\]
\[ = \frac{{20}}{9}.\frac{9}{{10}} - \frac{{46}}{5}.\frac{5}{{23}}\]
\( = \frac{{20.9}}{{9.10}} - \frac{{46.5}}{{5.23}}\)
= 2 – 2
= 0
d) \[\left( {4 - \frac{{12}}{{10}}} \right):2 + 30\% \]
\[ = \left( {4 - \frac{6}{5}} \right):2 + \frac{{30}}{{100}}\]
\( = \left( {\frac{{20}}{5} - \frac{6}{5}} \right):2 + \frac{3}{{10}}\)
\( = \frac{{14}}{5}.\frac{1}{2} + \frac{3}{{10}}\)
\( = \frac{{14}}{{10}} + \frac{3}{{10}}\)
\( = \frac{{17}}{{10}}\).
Câu 10:
Tìm \[x\].
a) x : 2,2 = (28,7 – 13,5).2 ;
b) \[\left( {3\frac{3}{4}.x + 75\% } \right):\frac{2}{3} = - 1\];
c) 4x – (3 + 5x) = 14
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
a) x : 2,2 = (28,7 – 13,5).2
x : 2,2 = 15,2 . 2
x : 2,2 = 30,4
x = 30,4 . 2,2
x = 66,88
Vậy x = 66,88
b) \[\left( {3\frac{3}{4}.x + 75\% } \right):\frac{2}{3} = - 1\]
\[\left( {\frac{{15}}{4}.x + \frac{{75}}{{100}}} \right):\frac{2}{3} = - 1\]
\[\left( {\frac{{15}}{4}.x + \frac{3}{4}} \right):\frac{2}{3} = - 1\]
\[\frac{{15}}{4}.x + \frac{3}{4} = \left( { - 1} \right).\frac{3}{2}\]
\[\frac{{15}}{4}.x + \frac{3}{4} = \frac{{ - 3}}{2}\]
\[\frac{{15}}{4}.x = \frac{{ - 3}}{2} - \frac{3}{4}\]
\[\frac{{15}}{4}.x = \frac{{ - 6}}{4} - \frac{3}{4}\]
\[\frac{{15}}{4}.x = \frac{{ - 9}}{4}\]
\(x = \frac{{ - 9}}{4}:\frac{{15}}{4}\)
\(x = \frac{{ - 9}}{4}.\frac{4}{{15}}\)
\(x = \frac{{ - 3}}{5}\)
Vậy \(x = \frac{{ - 3}}{5}.\)
c) 4x – (3 + 5x) = 14
4x – 3 – 5x = 14
4x – 5x = 14 + 3
– x = 17
x = –17
Vậy x = –17
Câu 11:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Số thóc thửa thứ nhất thu hoạch được là: \[15.\frac{7}{{20}} = \frac{{21}}{4}\] (tấn)
Số thóc thửa thứ hai thu hoạch được là: \[15.10\% = \frac{3}{2}\] (tấn)
Tổng số thóc thửa thứ nhất và thửa thứ hai thu hoạch được là: \[\frac{{21}}{4} + \frac{3}{2} = \frac{{27}}{4}\](tấn)
Số thóc thửa thứ ba thu hoạch được là: \[\frac{{27}}{4}.\frac{2}{5} = \frac{{27}}{{10}}\] (tấn)
Số thóc thửa thứ tư thu hoạch được là: \[15 - \left( {\frac{{21}}{4} + \frac{3}{2} + \frac{{27}}{{10}}} \right) = \frac{{111}}{{20}}\] (tấn).
Vậy thửa thứ tư thu hoạch được \(\frac{{111}}{{20}}\) tấn thóc.
Câu 12:
Cho điểm O thuộc đường thẳng xy. Trên tia Ox lấy điểm M sao cho OM = 4 cm. Trên tia Oy lấy điểm N sao cho ON = 2 cm. Gọi A, B lần lượt là trung điểm của OM và ON.
a) Chứng tỏ O nằm giữa A và B ;
b) Tính độ dài đoạn thẳng AB.
 Xem đáp án
Xem đáp án
Hướng dẫn giải :
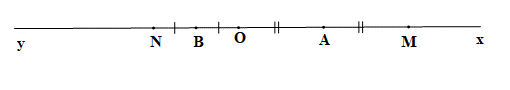
a) Vì O thuộc đường thẳng xy, mà điểm A thuộc tia Ox, điểm B thuộc tia Oy nên điểm O nằm giữa A và B.
b) Ta có A là trung điểm của OM nên \(OA = AM = \frac{{OM}}{2} = \frac{4}{2} = 2\) (cm)
Điểm B là trung điểm của ON nên \(OB = BN = \frac{{ON}}{2} = \frac{2}{2} = 1\) (cm).
Theo câu a, điểm O nằm giữa A và B nên AO + OB = AB.
Do đó AB = 2 + 1 = 3 (cm).
Vậy AB = 3 cm.
Câu 13:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
\[S = \frac{1}{{1.4}} + \frac{1}{{4.7}} + \frac{1}{{7.10}} + ... + \frac{1}{{94.97}} + \frac{1}{{97.100}}\]
\[3S = \frac{3}{{1.4}} + \frac{3}{{4.7}} + \frac{3}{{7.10}} + ... + \frac{3}{{94.97}} + \frac{3}{{97.100}}\]
\[3S = \frac{{4 - 1}}{{1.4}} + \frac{{7 - 4}}{{4.7}} + \frac{{10 - 7}}{{7.10}} + ... + \frac{{97 - 94}}{{94.97}} + \frac{{100 - 97}}{{97.100}}\]
\[3S = \left( {\frac{4}{{1.4}} - \frac{1}{{1.4}}} \right) + \left( {\frac{7}{{4.7}} - \frac{4}{{4.7}}} \right) + \left( {\frac{{10}}{{7.10}} - \frac{7}{{7.10}}} \right) + ... + \left( {\frac{{97}}{{94.97}} - \frac{{94}}{{94.97}}} \right) + \left( {\frac{{100}}{{97.100}} - \frac{{97}}{{97.100}}} \right)\]
\(3S = \left( {1 - \frac{1}{4}} \right) + \left( {\frac{1}{4} - \frac{1}{7}} \right) + \left( {\frac{1}{7} - \frac{1}{{10}}} \right) + ... + \left( {\frac{1}{{94}} - \frac{1}{{97}}} \right) + \left( {\frac{1}{{97}} - \frac{1}{{100}}} \right)\)
\(3S = 1 - \frac{1}{4} + \frac{1}{4} - \frac{1}{7} + \frac{1}{7} - \frac{1}{{10}} + ... + \frac{1}{{94}} - \frac{1}{{97}} + \frac{1}{{97}} - \frac{1}{{100}}\)
\(3S = 1 - \frac{1}{{100}}\)
\(3S = \frac{{100}}{{100}} - \frac{1}{{100}}\)
\(3S = \frac{{99}}{{100}}\)
Suy ra \(S = \frac{{99}}{{100}}:3\)
\(S = \frac{{99}}{{100}}.\frac{1}{3}\)
\(S = \frac{{33}}{{100}}\)
Vậy \(S = \frac{{33}}{{100}}\)
