Đề thi Cuối kì học kỳ 2 Toán 6 có đáp án (Đề 2)
-
2510 lượt thi
-
6 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Thực hiện phép tính (tính hợp lí nếu có thể):
a) (34,72 + 32,28) : 5 – (57,25 – 36,05) : 2;
b) \(8\frac{2}{7} - \left( {3\frac{4}{9} + 4\frac{2}{7}} \right)\);
c) \(\frac{5}{{13}} + \frac{{ - 5}}{7} + \frac{{ - 20}}{{41}} + \frac{8}{{13}} + \frac{{ - 21}}{{41}}\)
d) \(1\frac{{13}}{{15}}.0,75 - \left( {\frac{8}{{15}} + 25\% } \right)\)
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
a) (34,72 + 32,28) : 5 – (57,25 – 36,05) : 2;
= 67 : 5 + 21,2 : 2
= 13,4 – 10,6
= 2,8
b) \(8\frac{2}{7} - \left( {3\frac{4}{9} + 4\frac{2}{7}} \right)\);
\( = 8\frac{2}{7} - 3\frac{4}{9} - 4\frac{2}{7}\)
\( = \left( {8\frac{2}{7} - 4\frac{2}{7}} \right) - 3\frac{4}{9}\)
\( = \left[ {\left( {8 + \frac{2}{7}} \right) - \left( {4 + \frac{2}{7}} \right)} \right] - \left( {3 + \frac{4}{9}} \right)\)
\( = \left[ {\left( {8 - 4} \right) + \left( {\frac{2}{7} - \frac{2}{7}} \right)} \right] - \left( {3 + \frac{4}{9}} \right)\)
\( = 4 - 3 - \frac{4}{9}\)
\( = 1 - \frac{4}{9}\)
\( = \frac{9}{9} - \frac{4}{9}\)
\( = \frac{5}{9}\)
c) \(\frac{5}{{13}} + \frac{{ - 5}}{7} + \frac{{ - 20}}{{41}} + \frac{8}{{13}} + \frac{{ - 21}}{{41}}\)
\( = \left( {\frac{5}{{13}} + \frac{8}{{13}}} \right) + \left( {\frac{{ - 20}}{{41}} + \frac{{ - 21}}{{41}}} \right) + \frac{{ - 5}}{7}\)
\( = \frac{{13}}{{13}} + \frac{{ - 41}}{{41}} + \frac{{ - 5}}{7}\)
\( = 1 + \left( { - 1} \right) + \frac{{ - 5}}{7}\)
\( = 0 + \frac{{ - 5}}{7}\)
\( = \frac{{ - 5}}{7}\).
d) \(1\frac{{13}}{{15}}.0,75 - \left( {\frac{8}{{15}} + 25\% } \right)\)
\( = \frac{{28}}{{15}}.\frac{{75}}{{100}} - \left( {\frac{8}{{15}} + \frac{{25}}{{100}}} \right)\)
\[ = \frac{{4.7}}{{3.5}}.\frac{{3.25}}{{4.25}} - \left( {\frac{8}{{15}} + \frac{1}{4}} \right)\]
\( = \frac{7}{5} - \frac{8}{{15}} - \frac{1}{4}\)
\( = \frac{{84}}{{60}} - \frac{{32}}{{60}} - \frac{{15}}{{60}}\)
\( = \frac{{37}}{{60}}\)
Câu 2:
a) \(\frac{3}{5}x - \frac{1}{2} = \frac{1}{7}\)
b)
c) \[80\% + \frac{7}{6}:x = \frac{1}{6}\]
d) \(\frac{3}{4} - \left( {4\frac{1}{2} + 3x} \right) = - 1\)
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
a) \(\frac{3}{5}x - \frac{1}{2} = \frac{1}{7}\)
\(\frac{3}{5}x = \frac{1}{7} + \frac{1}{2}\)
\(\frac{3}{5}x = \frac{2}{{14}} + \frac{7}{{14}}\)
\(\frac{3}{5}x = \frac{9}{{14}}\)
\(x = \frac{9}{{14}}:\frac{3}{5}\)
\(x = \frac{9}{{14}}.\frac{5}{3}\)
\(x = \frac{{15}}{{14}}\)
Vậy \(x = \frac{{15}}{{14}}\).
b) \(\left( {4,5 - 2x} \right).\frac{{11}}{7} = \frac{{11}}{{14}}\)
\[\frac{9}{2} - 2x = \frac{{11}}{{14}}:\frac{{11}}{7}\]
\(\frac{9}{2} - 2x = \frac{{11}}{{14}}.\frac{7}{{11}}\)
\(\frac{9}{2} - 2x = \frac{1}{2}\)
\(2x = \frac{9}{2} - \frac{1}{2}\)
\(2x = \frac{8}{2}\)
2x = 4
x = 2.
Vậy x = 2.
c) \[80\% + \frac{7}{6}:x = \frac{1}{6}\]
\(\frac{{80}}{{100}} + \frac{7}{6} = \frac{1}{6}\)
\[\frac{4}{5} + \frac{7}{6}:x = \frac{1}{6}\]
\[\frac{7}{6}:x = \frac{1}{6} - \frac{4}{5}\]
\[\frac{7}{6}:x = \frac{5}{{30}} - \frac{{24}}{{30}}\]
\[\frac{7}{6}:x = \frac{{ - 19}}{{30}}\]
\[x = \frac{7}{6}:\frac{{ - 19}}{{30}}\]
\(x = \frac{7}{6}.\frac{{30}}{{ - 19}}\)
\[x = \frac{{ - 35}}{{19}}\]
Vậy \[x = \frac{{ - 35}}{{19}}\].
d) \(\frac{3}{4} - \left( {4\frac{1}{2} + 3x} \right) = - 1\)
\(4\frac{1}{2} + 3x = \frac{3}{4} - \left( { - 1} \right)\)
\(\frac{9}{2} + 3x = \frac{3}{4} + 1\)
\(\frac{9}{2} + 3x = \frac{3}{4} + \frac{4}{4}\)
\(\frac{9}{2} + 3x = \frac{7}{4}\)
\(3x = \frac{9}{2} - \frac{7}{4}\)
\(3x = \frac{{18}}{4} - \frac{7}{4}\)
\(3x = \frac{{11}}{4}\)
\(x = \frac{{11}}{4}:3\)
\(x = \frac{{11}}{4}.\frac{1}{3}\)
\(x = \frac{{11}}{{12}}\)
Vậy \(x = \frac{{11}}{{12}}\).\(\)
Câu 3:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Ngày thứ nhất bạn An làm được \(\frac{2}{3}\) tổng số bài.
Ngày thứ hai bạn An làm được \(20\% \) tổng số bài, hay số bài làm được là \(\frac{{20}}{{100}} = \frac{1}{5}\) tổng số bài.
Vậy sau ngày thứ nhất và ngày thứ hai An làm được: \(\frac{2}{3} + \frac{1}{5} = \frac{{13}}{{15}}\) tổng số bài.
Vậy ngày thứ ba còn \(1 - \frac{{13}}{{15}} = \frac{2}{{15}}\) tổng số bài.
Ngày thứ ba bạn An làm nốt \(2\) bài nên ta có số bài làm trong ba ngày là:
\(2:\frac{2}{{15}} = 15\) bài.
Vậy tổng số bài bạn An làm là 15 bài.
Câu 4:
Gieo con xúc xắc có 6 mặt 100 lần, kết quả thu được ghi ở bảng sau:
|
Mặt |
1 chấm |
2 chấm |
3 chấm |
4 chấm |
5 chấm |
6 chấm |
|
Số lần xuất hiện |
17 |
18 |
15 |
14 |
16 |
20 |
a) Trong 100 lần gieo xúc xắc thì mặt nào xuất hiện nhiều nhất? Mặt nào xuất hiện ít nhất?
b) Hãy tìm xác suất của thực nghiệm của các sự kiện gieo được mặt có chấm chẵn?
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
a) Trong 100 lần gieo xúc xắc thì mặt 6 chấm xuất hiện nhiều nhất và mặt 4 chấm xuất hiện ít nhất.
b) Các mặt có số chẵn chấm của con xúc xắc là mặt 2 chấm, 4 chấm, 6 chấm.
Tổng số lần xuất hiện mặt chấm chẵn là: 18 + 14 + 20 = 52 (lần).
Xác suất của thực nghiệm của các sự kiện gieo được mặt có chấm chẵn là: \(\frac{{52}}{{100}} = 0,52.\)
Vậy xác suất của thực nghiệm của các sự kiện gieo được mặt có chấm chẵn là: 0,52.
Câu 5:
1. Hình nào trong các hình sau có trục đối xứng đồng thời có tâm đối xứng?

2.
a) Vẽ góc xOy có số đo bằng 55°. Góc xOy là góc nhọn, góc vuông hay góc tù?
b) Trên Ox lấy hai điểm A, B sao cho OA = 2 cm, OB = 6 cm. Gọi \(M\) là trung điểm của đoạn thẳng AB. Tính AM.
 Xem đáp án
Xem đáp án
Hướng dẫn giải
1. Trong các hình trên thì Hình 1 là hình vừa có trục đối xứng vừa có tâm đối xứng.
2.
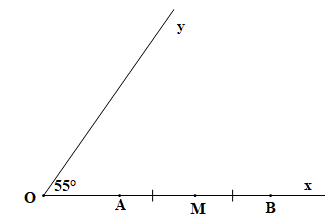
a) Góc xOy có số đo bằng 55° mà 55° < 90°
Do đó góc xOy là góc nhọn.
b) Trên \[{\rm{Ox}}\] lấy hai điểm A, B: OA = 2 cm, OB = 6 cm (OA < OB) nên điểm A nằm giữa hai điểm O và B.
Do đó OA + AB = OB.
Suy ra AB = OB – OA
Hay AB = 6 – 2 = 4 cm.
Vì M là trung điểm của đoạn thẳng OB nên \(AM = MB = \frac{{AB}}{2} = \frac{4}{2} = 2\) cm.
Câu 6:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Ta có: \[B = \frac{{10n - 3}}{{4n - 10}} = \frac{{2,5\left( {4n - 10} \right) + 22}}{{4n - 10}}\]
\[ = \frac{{2,5\left( {4n - 10} \right)}}{{4n - 10}} + \frac{{22}}{{4n - 10}} = 2,5 + \frac{{22}}{{4n - 10}}\]
Vì n là số tự nhiên nên \[B = 2,5 + \frac{{22}}{{4n - 10}}\] đạt giá trị lớn nhất khi \[\frac{{22}}{{4n - 10}}\] đạt đạt giá trị lớn nhất.
Mà \[\frac{{22}}{{4n - 10}}\] đạt đạt giá trị lớn nhất khi 4n – 10 là số nguyên dương nhỏ nhất.
+) Nếu 4n – 10 = 1 thì 4n = 11 hay \(n = \frac{{11}}{4}\) (loại)
+) Nếu 4n – 10 = 2 thì 4n = 12 hay n = 3 (chọn)
Khi đó \(B = 2,5 + \frac{{22}}{2} = 13,5\)
Vậy B đạt giá trị lớn nhất là 13,5 khi n = 3.
