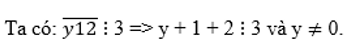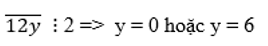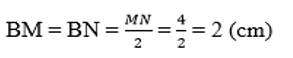10 câu hỏi trắc nghiệm thuộc Đề thi Học kì 1 Toán 6 cực hay có đáp án (Đề 4)

Đề thi Học kì 1 Toán 6 cực hay có đáp án (Đề 4)

Đề số 1

Đề thi Học kì 1 Toán 6 cực hay có đáp án (Đề 4)

417 lượt thi
10 câu hỏi
30 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

a) Viết tập hợp X các số tự nhiên x thỏa mãn: x chia hết cho 4 và 2010 < x < 2025

Xem đáp án

a) X = {2012 ; 2016 ; 2020 ; 2024}

Câu 2:

b) Cho y ∈ { 0; 1; 2; 3; 4; 5; 6 }. Thay y bằng chữ số thích hợp để:

$\bar{y 12}$ chia hết cho 3

$\bar{12 y}$ chia hết cho cả 2 và 3

Xem đáp án

y + 3 ⋮ 3 => y ⋮ 3

Mà: y ∈ {0 ; 1 ; 2 ; 3 ; 4 ; 5 ; 6} và y ≠ 0 nên y ∈ {3 ; 6}.

Vậy số cần tìm là 312 ; 612.

Vậy số cần tìm là 120 ; 126.

Câu 3:

a) Thực hiện phép tính: 2011 : { 639 : [ 316 – ( 78 + 25 )] : 3 }

Xem đáp án

a) 2011 : { 639 : [ 316 – ( 78 + 25 )] : 3 }

= 2011 : { 639 : [ 316 – 103 ] : 3}

= 2011 : ( 639 : 213 : 3 ) = 2011 : (3 : 3 ) = 2011 : 1 = 2011

Câu 4:

b) Tìm số tự nhiên x, biết: ( 3x – $2^{3}$ ) . 7 = $7^{4}$

Xem đáp án

b) ( 3x – $2^{3}$ ) . 7 = $7^{4}$

3x – 8 = $7^{4}$ : 7

3x – 8 = $7^{3}$

3x – 8 = 343

3x = 343 + 8

3x = 351

x = 351 : 3 = 117

Câu 5:

c) Tìm số tự nhiên x, biết: ( 8705 + 5235 ) – 5x = 3885.

Xem đáp án

c) (8705 + 5235) – 5x = 3885

13940 – 5x = 3885

5x = 13940 – 3885

5x = 10055

x = 10055 : 5 = 2011

Câu 6:

Tính số dư khi chia:

( $2^{1} + 2^{2} + 2^{3} + 2^{4} + . . . + 2^{99} + 2^{100}$ ) cho 7

Xem đáp án

Ta có

$2^{1}$ + $2^{2} + 2^{3} + 2^{4}$ + $2^{5} + 2^{6} + 2^{7}$ +...+ $2^{98} + 2^{99} + 2^{100}$

= $2^{1}$ + ( $2^{2} + 2^{3} + 2^{4}$ ) + ( $2^{5} + 2^{6} + 2^{7}$ ) +...+ ( $2^{98} + 2^{99} + 2^{100}$ )

$= 2 + 2^{2} (1 + 2 + 2^{2}) + 2^{5} (1 + 2 + 2^{2}) + . . . + 2^{98} (1 + 2 + 2^{2})$

$= 2 + 2^{2} . 7 + 2^{5} . 7 + . . . + 2^{98} . 7 = 2 + 7 (2^{2} + 2^{5} + . . . + 2^{98})$

Mà $7 . (2^{2} + 2^{5} + . . . + 2^{98}) ⋮ 7$

Nên $2 + 7 (2^{2} + 2^{5} + . . . + 2^{98}) : 7 d ư 2$

Câu 7:

Một trường tổ chức cho khoảng từ 800 đến 950 học sinh khối 6 và khối 8 đi tham quan. Tính số học sinh đi tham quan, biết rằng nếu xếp hàng 20, 25, 30 đều thừa ba học sinh, nhưng khi xếp hàng 43 thì vừa đủ.

Xem đáp án

Gọi số học sinh khối 6 và khối 8 đi tham quan là x (800 ≤ x ≤ 950)

Ta có: x – 3 là bội chung của 20 ; 25 ; 30 và 797 ≤ x – 3 ≤ 947

BCNN( 20 ; 25 ; 30 ) = 300

⇒ BC( 20 ; 25 ; 30 ) = B(300) = { 0 ; 300 ; 600 ; 900 ; ... }

Do đó: x – 3 ∈ { 0 ; 300 ; 600 ; 900 ; ... } ⇒ x ∈ { 3 ; 303 ; 603 ; 903 ; ... }

Mà 800 ≤ x ≤ 950 và chia hết cho 43 nên x = 903.

Vậy số học sinh khối 6 và khối 8 đi tham quan là 903 học sinh.

Câu 8:

Vẽ đoạn thẳng MN dài 4 cm. Lấy điểm A nằm giữa M và N sao cho MA = 3cm.

a) Tính độ dài đoạn thẳng AN

Xem đáp án