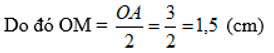Đề thi Học kì 1 Toán 6 cực hay có đáp án (Đề 5)
-
1660 lượt thi
-
11 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Tính bằng cách hợp lý (nếu có thể)
a) (-21) + | -50 | + (-29) – | -2016 |
Xem đáp án
a) (-21) + |-50| + (-29) – |-2016|
= (-21) + 50 + (-29) – 2016
= [(-21) + (-29) + 50] – 2016 = ( -50 +50 ) – 2016
= 0 – 2016 = - 2016 .
Câu 2:
Tính bằng cách hợp lý (nếu có thể)
b) 36 : + . -
Xem đáp án
b) 36 : -150
= 36 : 9 + 9 . 8 – 1 = 4 + 72 – 1 = 76 – 1 = 75
Câu 3:
Tính bằng cách hợp lý (nếu có thể)
c) ( ) : ( )
Xem đáp án
c) () : ( )
= ( ) : [ . ( 26 – 1)]
= ( ) : ( . 25 )
= ( 52 – 51 – 50) : ( . 52 )
= ( . 19 ) : = 19
Câu 4:
a) 115 + 5 ( x – 4 ) = 120
Xem đáp án
a) 115 + 5 ( x – 4 ) = 120
5 ( x – 4 ) = 120 – 115
5 ( x – 4 ) = 5
x – 4 = 5 : 5
x – 4 = 1
x = 1 + 4
x = 5
Câu 5:
b) 5|x| – =
Xem đáp án
b) 5| x | – =
5| x | – 1 =
5| x | = 9 + 1
5| x | = 10
| x | = 2
x = 2 hoặc x = -2
Câu 7:
Cho A = {x ∈ N / 24 ⋮ x, 60 ⋮ x và 5 ≤ x ≤ 10}. Viết tập hợp A bằng cách liệt kê các phần tử.
Xem đáp án
Ta có 24 ⋮ x , 30 ⋮ x , 60 ⋮ x
x ∈ ƯC (24, 30, 60)
24 = 23 . 3 , 30 = 2 . 3 . 5 ; 60 = 22 . 3 . 5
ƯCLN (24, 30, 60) = 2 . 3 = 6. Nên x ∈ ƯC( 6 )
Do đó x ∈ { 1; 2; 3; 6 }
Mà 5 ≤ x ≤ 10. Nên x = 6.
Vậy A = { 6 }
Câu 8:
Số học sinh khối 6 của một trường chưa đến 200 học sinh. Biết rằng khi xếp hàng 4, hàng 5 hay hàng 6 thì đều thiếu 1 học sinh nhưng xếp hàng 7 thì vừa đủ. Tìm số học sinh khối 6 của trường đó.
Xem đáp án
Gọi số học sinh khối 6 của trường đó là x (học sinh) (x ∈ N*)
Theo đề bài khi xếp hàng 4, hàng 5, hàng 6 đều thiếu 1 học sinh nên x + 1 chia hết cho 4, 5, 6. Mặt khác xếp hàng 7 thì vừa đủ nên x ⋮ 7. Mà số học sinh chưa đến 200 học sinh nên x < 200.
BCNN ( 4, 5, 6 ) = 60
BC ( 4, 5, 6 ) = B ( 60 ) = { 0; 60; 120; 180; 240; … }
Từ đó x + 1 ∈ { 60; 120; 180; 240; … }
Do đó x ∈ { 59; 119; 179; 239; … }
Mà x < 200. Nên x = 119 hoặc x = 179
Ta có 119 = 17 . 7 ; 179 không chia hết cho 7
Vậy x = 119 thích hợp
Số học sinh khối 6 của trường đó là 119 học sinh.
Câu 9:
Trên tia Ox lấy hai điểm A và B sao cho OA = 3cm, OB = 5 cm.
a) Tính AB
Xem đáp án
a) Trên tia Ox có A, B và OA < OB (và 3cm < 5cm). Do đó điểm A nằm giữa hai điểm O và B
Ta có OA + AB = OB
3 + AB + 5
AB = 5 – 3
AB = 2 (cm)
Câu 10:
Trên tia Ox lấy hai điểm A và B sao cho OA = 3cm, OB = 5 cm.
b) Lấy điểm C thuộc tia đối của tia BA sao cho BC = 2cm. Chứng tỏ B là trung điểm của AC.
Xem đáp án
b) Ta có B nằm giữa A và C
AB = BC ( = 2cm)
Do đó B là trung điểm của AC
Câu 11:
Trên tia Ox lấy hai điểm A và B sao cho OA = 3cm, OB = 5 cm.
c) Lấy điểm M là trung điểm của OA. Tính MC.
Xem đáp án
c) Ta có M là trung điểm của OA
Ta có B nằm giữa O và C
Do đó OC = OB + BC
OC = 5 + 2
OC = 7 (cm)
Mà M nằm giữa O và C
Do đó OM + MC = OC
1,5 + MC = 7
MC + 7 – 1,5
MC = 5,5 (cm)