Đề thi Toán lớp 6 Giữa kì 1 có đáp án (Đề 1)
-
964 lượt thi
-
9 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 2:
Trong các số tự nhiên sau số nào là số nguyên tố?
Xem đáp án
Trong 4 đáp án chỉ có số 2 là chia hết cho 1 và chính nó. Nên 2 là số nguyên tố.
Chọn đáp án D.
Câu 3:
Trong hình vuông, khẳng định nào sau đây là đúng?
Xem đáp án
Hình vuông có 4 cạnh bằng nhau và 4 góc bằng nhau (4 góc vuông). Theo tính chất, hai đường chéo hình vuông bằng nhau, vuông góc và giao nhau tại trung điểm của mỗi đường.
Chọn đáp án C.
Câu 4:
Cho các số tự nhiên a, m, n khẳng định nào sau đây đúng?
Xem đáp án
Khẳng định đúng là am.an = am + n .
Chọn đáp án B.
Câu 5:
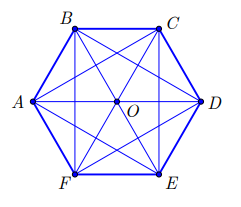
Cho hình lục giác đều như hình vẽ, số hình tam giác đều có các đỉnh là 3 trong 7 điểm A, B, C, D, E, F, O là
Xem đáp án
Số tam giác đều là: 8 hình
Đó là: AOB, BOC, COD, DOE, EOF, FOA, ACE, BDF.
Chọn đáp án B.
Câu 6:
Có bao nhiêu chữ số a để \(\overline {57a} \) chia hết cho 3 ?
Xem đáp án
Ta có: 5 + 7 + a = 12 + a
Để \(\overline {57a} \) chia hết cho 3 thì (12 + a) phải chia hết cho 3.
Các chữ số a thỏa mãn là 0, 3, 6, 9.
Vậy có 4 chữ số a thỏa mãn,
Chọn đáp án B.
Câu 7:
1) Viết tập hợp A các số x chia hết cho 5, thỏa mãn 124 < x < 145 bằng cách liệt kê các phần tử. Tìm kí hiệu thích hợp (∈, ∉) thay cho dấu “?”
145 ? A135 ? A
2) Thực hiện phép tính nếu có thể
a) 62.28 + 72.62
b) 600 : {450 : [450 – (4.53 – 23.52)]}
Xem đáp án
1) Tập hợp A các số x chia hết cho 5, thỏa mãn 124 < x < 145 là:
A = {125; 130; 135; 140}
Kí hiệu thay cho dấu ? là:
145 ∉ A135 ∈ A
2)
a) 62.28 + 72.62
= 62.(28 + 72)
= 36.100
= 3600
b) 600 : {450 : [450 – (4.53 – 23.52)]}
= 600 : {450 : [450 – (4.125 – 8.25)]}
= 600 : [450 : (450 – 300)]
= 600 : (450 : 150)
= 600 : 3
= 200
Câu 8:
1) Tìm x ∈ {24; 36; 42; 132} để x + 60 không chia hết cho 12.
2) Để phòng chống dịch Covid-19, thành phố Bắc Ninh đã thành lập các đội phản ứng nhanh bao gồm các bác sĩ hồi sức cấp cứu, bác sĩ đa khoa và điều dưỡng viên. Biết rằng có tất cả 18 bác sĩ hồi sức cấp cứu, 27 bác sĩ đa khoa và 45 điều dưỡng viên. Hỏi có thể thành lập được nhiều nhất bao nhiêu đội phản ứng nhanh, trong đó số bác sĩ hồi sức cấp cứu, bác sĩ đa khoa và điều dưỡng viên được chia đều vào mỗi đội?
Xem đáp án
1) Vì x + 60 không chia hết cho 12
Mà 60 ⁝ 12 nên x không chia hết cho 12
Mà x ∈ {24; 36; 42; 132}, trong số đó có 42 không chia hết cho 12 nên x = 42.
Vậy x = 42 để x + 60 không chia hết cho 12.
2) Gọi số đội phản ứng nhanh là x (đội, \(x \in {\mathbb{N}^*}\)).
Để số bác sĩ hồi sức cấp cứu, bác sĩ đa khoa và điều dưỡng viên được chia đều vào mỗi đội và số đội là lớn nhất thì x = ƯCLN(18, 27, 45)
18 = 2.32
27 = 33
45 = 5.32
ƯCLN(18, 27, 45) = 32 = 9 hay x = 9 (tm).
Vậy có thể lập được nhiều nhất 9 đội phản ứng nhanh.
Câu 9:
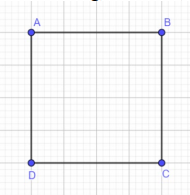
1) Vẽ hình vuông ABCD có cạnh 4 cm.
2) Nối các điểm chính giữa mỗi cạnh của hình vuông đó thì được hình vuông thứ hai; nối các điểm chính giữa mỗi cạnh của hình vuông thứ hai ta được hình vuông thứ ba; tiếp tục vẽ như thế. Hỏi vẽ đến hình vuông thứ bao nhiêu thì ta được 120 hình tam giác.
Xem đáp án
1) Sử dụng ê ke để vẽ:
- Vẽ theo một cạnh góc vuông của ê ke đoạn thẳng AB = 4 cm.
- Đặt đỉnh góc vuông của ê ke trùng với điểm A và một cạnh ê ke nằm trên AB, vẽ theo cạnh kia của ê ke đoạnh thẳng AD = 4 cm.
- Xoay ê ke rồi thực hiện tương tự như Bước 2để được cạnh BC = 4 cm.
- Vẽ đoạn thẳng CD, ta được hình vuông ABCD có cạnh bằng 4 cm.
2)
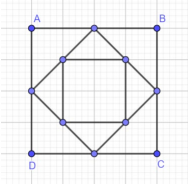
Vẽ hình vuông thứ 1 được 4.0 = 0 tam giác
Vẽ hình vuông thứ 2 được 4.1 = 4 tam giác
Vẽ hình vuông thứ 3 được 4.2 = 8 tam giác
…
Vẽ hình vuông thứ n được 4.n = n tam giác
Theo bài ra ta có:
4.(n – 1) = 120
n – 1 = 120 : 4
n – 1 = 30
n = 30 + 1
n = 31
Vậy đến hình vuông thứ 31 ta sẽ được 120 hình tam giác.