Bài 7: Bài tập cuối chương 2 - Bộ Cánh diều
-
2174 lượt thi
-
8 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Sử dụng số nguyên âm để thể hiện các tình huống sau:
a) Nợ 150 nghìn đồng;
b) 600 m dưới mực nước biển;
c) 12 độ dưới 0 °C.
Xem đáp án
a) Nợ 150 nghìn đồng có nghĩa là có – 150 nghìn đồng.
b) 600 m dưới mực nước biển có nghĩa là độ cao so với mực nước biển là – 600 m.
c) 12 độ dưới 0 °C có nghĩa nhiệt độ hiện tại ở đây là – 12 °C.
Câu 2:
Trong Hình 10, hãy tính (theo mét):
a) Khoảng cách giữa ặng san hô và người thợ lặn;
b) Khoảng cách giữa người thợ lặn và mặt nước;
c) Khoảng cách giữa mặt nước và con chim;
d) Khoảng cách giữa rặng san hô và con chim.
Xem đáp án
Quan sát Hình 10 trên trục mét, ta thấy:
+ Rặng san hô tương ứng với vị trí – 3 m
+ Người thợ lặn tương ứng với vị trí – 2 m
+ Mặt nước tương ứng với vị trí 0 m
+ Con chim tương ứng với vị trí 4 m
Do đó ta có:
a) Khoảng cách giữa rặng san hô và người thợ lặn là: (– 2) – (– 3) = 1 (m)
b) Khoảng cách giữa người thợ lặn và mặt nước là: 0 – (– 2) = 2 (m)
c) Khoảng cách giữa mặt nước và con chim là: 4 – 0 = 4 (m)
d) Khoảng cách giữa rặng san hô và con chim là: 4 – (– 3) = 7 (m).
Câu 3:
Quan sát trục số sau:
a) Các điểm N, B, C biểu diễn những số nào?
b) Điểm nào biểu diễn số – 7?
Xem đáp án
Hoàn thành trục số đã cho ta được:
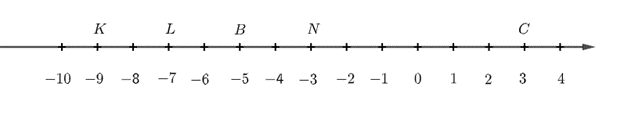
a) Khi đó ta có:
+ Điểm N biểu diễn số – 3
+ Điểm B biểu diễn số – 5
+ Điểm C biểu diễn số 3.
b) Điểm biểu diễn số – 7 là điểm L.
Câu 4:
Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai? Giải thích.
a) Kết quả của phép trừ số nguyên dương cho số nguyên dương là số nguyên dương.
b) Kết quả của phép trừ số nguyên dương cho số nguyên âm là số nguyên dương.
c) Kết quả của phép nhân số nguyên dương với số nguyên âm là số nguyên âm.
Xem đáp án
a) Kết quả của phép trừ số nguyên dương cho số nguyên dương là số nguyên dương là phát biểu sai.
Ta có thể lấy ví dụ như sau:
Với hai số nguyên dương là 7 và 10 ta thực hiện phép trừ
7 – 10 = 7 + (– 10) = – 3 < 0
Ta được kết quả là – 3, đây là một số nguyên âm, không phải số nguyên dương.
b) Kết quả của phép trừ số nguyên dương cho số nguyên âm là số nguyên dương là phát biểu đúng.
Thật vậy, giả sử ta có số nguyên dương a bất kì đóng vai trò là số bị trừ và số nguyên âm – b đóng vai trò là số trừ. Khi đó ta thực hiện phép trừ:
a – (– b) = a + b
Vì – b là số nguyên âm, nên số đối của nó là b là một số nguyên dương
Do đó tổng a + b là một số nguyên dương, hay kết quả của phép trừ a – (– b) là một số nguyên dương.
c) Ta có tích hai số nguyên khác dấu là số nguyên âm.
Do đó kết quả của phép nhân số nguyên dương với số nguyên âm là số nguyên âm là phát biểu đúng.
i số nguyên âm là số nguyên âm.
Câu 5:
Tính:
a) (– 15) . 4 – 240 : 6 + 36 : (– 2) . 3;
b) (– 25) + [(– 69) : 3 + 53)] . (– 2) – 8.
Xem đáp án
a) (– 15) . 4 – 240 : 6 + 36 : (– 2) . 3
= – (15 . 4) – 40 + [– (36 : 2) . 3]
= (– 60) – 40 + [(– 18) . 3]
= (– 60) – 40 + (– 54)
= (– 60) + (– 40) + (– 54)
= – (60 + 40 + 54)
= – 154.
b) (– 25) + [(– 69) : 3 + 53] . (– 2) – 8
= (– 32) + [– (69 : 3) + 53] . (– 2) – 8
= (– 32) + [ (– 23) + 53] . (– 2) – 8
= (– 32) + (53 – 23) . (– 2) – 8
= (– 32) + 30 . (– 2) – 8
= (– 32) + (– 60) – 8
= – (32 + 60) – 8
= – 92 – 8
= – (92 + 8)
= – 100.
Câu 6:
Tìm số nguyên x, biết:
a) 4 . x + 15 = – 5;
b) (– 270) : x – 20 = 70.
Xem đáp án
a) 4 . x + 15 = – 5
4 . x = (– 5) – 15
4 . x = – 20
x = (– 20) : 4
x = – 5
Vậy x = – 5.
b) (– 270) : x – 20 = 70
(– 270) : x = 70 + 20
(– 270) : x = 90
x = (– 270) : 90
x = – 3
Vậy x = – 3.
Câu 7:
Công ty An Bình có lợi nhuận ở mỗi tháng trong 4 tháng đầu năm là – 70 triệu đồng. Trong 8 tháng tiếp theo lợi nhuận mỗi tháng của công ty là 60 triệu đồng. Sau 12 tháng kinh doanh, lợi nhuận của công ty An Bình là bao nhiêu tiền?
Xem đáp án
Cách 1.
Lợi nhuận của công ty An Bình trong 4 tháng đầu năm là:
– 70 . 4 = – 280 (triệu đồng)
Lợi nhuận của công ty An Bình trong 8 tháng tiếp theo là:
60 . 8 = 480 (triệu đồng)
Sau 12 tháng kinh doanh, lợi nhuận của công ty An Bình là:
(– 280) + 480 = 200 (triệu đồng)
Vậy sau 12 tháng kinh doanh, lợi nhuận của công ty An Bình là 200 triệu đồng.
Cách 2. (làm gộp)
Lợi nhuận của công ty An Bình sau 12 tháng kinh doanh là:
(– 70) . 4 + 60 . 8 = 200 (triệu đồng)
Vậy sau 12 tháng kinh doanh, lợi nhuận của công ty An Bình là 200 triệu đồng.
Câu 8:
Người ta sử dụng biểu thức T = (I – E) : 12 để biểu diễn số tiền tiết kiệm trung bình mỗi tháng của một người, trong đó I là tổng thu nhập và E là tổng chi phí trong một năm của người đó. Bác Dũng có số tiền tiết kiệm trung bình mỗi tháng là 3 triệu đồng và tổng chi phí cả năm là 84 triệu đồng. Tính tổng thu nhập cả năm của bác Dũng.
Xem đáp án
Bác Dũng có số tiền tiết kiệm trung bình mỗi tháng là 3 triệu đồng hay T = 3 triệu đồng.
Tổng chi phí cả năm của bác là 84 triệu đồng, hay E = 84 triệu đồng
Ta cần tìm tổng thu nhập I cả năm của bác Dũng.
Khi đó ta có biểu thức T = (I – E) : 12 với T = 3, E = 84
Thay T = 3 và E = 84 vào biểu thức trên ta được:
3 = (I – 84) : 12
Hay (I – 84) : 12 = 3
I – 84 = 3 . 12
I – 84 = 36
I = 36 + 84
I = 120.
Vậy tổng thu nhập cả năm của bác Dũng là 120 triệu đồng.