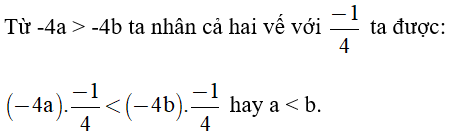Bài 2: Liên hệ giữa thứ tự và phép nhân
-
2279 lượt thi
-
14 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
a) Nhân cả hai vế của bất đẳng thức -2 < 3 với 5091 thì được bất đẳng thức nào ?
b) Dự đoán kết quả: Nhân cả hai vế của bất đẳng thức -2 < 3 với số c dương thì ta được bất đẳng thức nào ?
Xem đáp án
a) - 2. 5091 = - 10 182 và 3. 5091 = 15 273
⇒ - 10 182 < 15 273
b) Nhân cả hai vế của bất đẳng thức -2 < 3 với số c dương thì ta được bất đẳng thức: -2c < 3c
Câu 2:
Đặt dấu thích hợp (<, >) vào ô vuông:
a) Vì – 15,2 < - 15,08 và 3,5 > 0 nên:
(-15,2) . 3,5 .....(-15,08) . 3,5;
b) Vì 4,15 > - 5,3 và 2,2 > 0 nên:
4,15 . 2,2 ..... (-5,3) . 2,2.
Xem đáp án
a) (-15,2) . 3,5 < (-15,08) . 3,5
b) 4,15 . 2,2 > (-5,3) . 2,2
Câu 3:
a) Nhân cả hai vế của bất đẳng thức -2 < 3 với -345 thì được bất đẳng thức nào ?
b) Dự đoán kết quả: Nhân cả hai vế của bất đẳng thức -2 < 3 với số c âm thì ta được bất đẳng thức nào ?
Xem đáp án
a) (-2) . (- 345) = 690; 3 .(-345) = - 1035
⇒ 690 > - 1035
b) Nhân cả hai vế của bất đẳng thức -2 < 3 với số c âm thì ta được bất đẳng thức: -2c > 3c
Câu 5:
Mỗi khẳng định sau đúng hay sai? Vì sao?
a) (-6).5 < (-5).5 ;
b) (-6).(-3) < (-5).(-3);
c) (-2003).(-2005) ≤ (-2005).2004;
d) -3x2 ≤ 0.
Xem đáp án
a) Ta có: -6 < -5
⇒ (-6).5 < (-5).5 (Nhân cả hai vế với 5 > 0 được BĐT cùng chiều).
⇒ Khẳng định a) đúng.
b) -6 < -5
⇒ (-6).(-3) > (-5).(-3) (Nhân cả hai vế với -3 < 0, BĐT đổi chiều).
⇒ Khẳng định b) sai.
c) -2003 < 2004
⇒ (-2003).(-2005) > (-2005).2004 (Nhân cả hai vế với -2005 < 0, BĐT đổi chiều)
⇒ Khẳng định c) sai.
d) x2 ≥ 0 với mọi x ∈ R.
⇒ (-3).x2 ≤ (-3).0 (Nhân cả hai vế với -3 < 0, BĐT đổi chiều).
hay -3x2 ≤ 0.
⇒ Khẳng định d) đúng với mọi số thực x.
Kiến thức áp dụng
Khi nhân cả hai vế của BĐT với cùng một số c khác 0 ta được BĐT mới:
+ Cùng chiều với BĐT đã cho nếu c > 0
+ Ngược chiều với BĐT đã cho nếu c < 0.
Cho a < b, c ≠ 0, ta có:
+ ac < bc nếu c > 0
+ ac > bc nếu c < 0.
Câu 6:
Cho a < b, hãy so sánh: 2a và 2b; 2a và a + b; -a + b; -a và -b.
Xem đáp án
+ a < b ⇒ 2a < 2b (nhân cả hai vế với 2 > 0, BĐT không đổi chiều).
+ a < b ⇒ a + a < b + a (Cộng cả hai vế với a)
hay 2a < a + b.
+ a < b ⇒ (-1).a > (-1).b (Nhân cả hai vế với -1 < 0, BĐT đổi chiều).
hay –a > -b.
Kiến thức áp dụng
Khi nhân cả hai vế của BĐT với cùng một số c khác 0 ta được BĐT mới:
+ Cùng chiều với BĐT đã cho nếu c > 0
+ Ngược chiều với BĐT đã cho nếu c < 0.
Nếu a < b, c ≠ 0, thì ac < bc với c > 0 ; ac > bc với c < 0.
Khi cộng cùng một số vào cả hai vế của một bất đẳng thức ta được một bất đẳng thức mới cùng chiều với bất đẳng thức đã cho.
Nếu a < b thì a + c < b < c.
Câu 7:
Số a là số âm hay dương nếu: 12a < 15 a ? 4a < 3a ? -3a > -5a?
Xem đáp án
a) Ta có: 12 < 15 (*). Để có bất đẳng thức cùng chiều là 12a < 15a ta phải nhân cả hai vế của (*) với số dương. Vậy a là số dương.
b) Ta có: 4 > 3 (**). Để có bất đẳng thức ngược chiều là 4a < 3a ta phải nhân cả hai vế của (**) với số âm. Vậy a là số âm.
c) Ta có: -3 > -5 (***). Để có bất đẳng thức cùng chiều là -3a > -5a ta phải nhân cả hai vế của (***) với số dương. Vậy a là số dương.
Kiến thức áp dụng
Khi nhân cả hai vế của BĐT với cùng một số c khác 0 ta được BĐT mới:
+ Cùng chiều với BĐT đã cho nếu c > 0
+ Ngược chiều với BĐT đã cho nếu c < 0.
Nếu a < b, c ≠ 0, thì ac < bc với c > 0 ; ac > bc với c < 0.
Câu 8:
Cho a < b, chứng tỏ: a) 2a - 3 < 2b - 3; b) 2a - 3 < 2b + 5.
Xem đáp án
a) Ta có: a < b
⇒ 2a < 2b (Nhân cả hai vế với 2 > 0, BĐT không đổi chiều).
⇒ 2a – 3 < 2b – 3 (Cộng cả hai vế với -3, BĐT không đổi chiều).
Vậy 2a – 3 < 2b – 3.
b) Ta có: -3 < 5
⇒ 2b - 3 < 2b + 5 (cộng vào hai vế với 2b)
mà 2a - 3 < 2b - 3 (chứng minh ở câu a))
Vậy: 2a - 3 < 2b + 5 (Tính chất bắc cầu).
Kiến thức áp dụng
Khi nhân cả hai vế của BĐT với cùng một số c khác 0 ta được BĐT mới:
+ Cùng chiều với BĐT đã cho nếu c > 0
+ Ngược chiều với BĐT đã cho nếu c < 0.
Nếu a < b, c ≠ 0, thì ac < bc với c > 0; ac > bc với c < 0.
Khi cộng cùng một số vào cả hai vế của một bất đẳng thức ta được một bất đẳng thức mới cùng chiều với bất đẳng thức đã cho.
Nếu a < b thì a + c < b < c.
Tính chất bắc cầu: Nếu a < b và b < c thì a < c.
Câu 9:
Cho tam giác ABC. Các khẳng định sau đúng hay sai?
Xem đáp án
Theo định lí tổng ba góc trong tam giác thì Â + B̂ + Ĉ = 180º
Do đó:
a) Â + B̂ + Ĉ > 180º là sai.
b)  + B̂ = 180º - Ĉ < 180º nên khẳng định  + B̂ < 180º là đúng.
c) Ĉ + B̂ = 180º - Â ≤ 180º nên khẳng định Ĉ + B̂ ≤ 180º là đúng.
d)  + B̂ < 180º nên khẳng định  + B̂ ≥ 180º là sai.
Kiến thức áp dụng
+ Trong một tam giác, tổng của ba góc trong bằng 180º.
Câu 10:
a) So sánh (-2).3 và -4,5.
b) Từ kết quả câu a) hãy suy ra các bất đẳng thức sau:
(-2).30 < -45 ; (-2).3 + 4,5 < 0
Xem đáp án
a) Ta có : (-2).3 = -6.
Vì -6 < -4,5 nên suy ra (-2).3 < -4,5.
b) + Ta có : (-2).3 < -4,5
⇒ (-2).3.10 < -4,5.10 (Nhân cả hai vế với 10 > 0, BĐT không đổi chiều).
hay (-2).30 < -45.
+ (-2).3 < -4,5
⇒ (-2).3 + 4,5 < -4,5 + 4,5 (Cộng cả hai vế với 4,5).
Hay (-2).3 + 4,5 < 0.
Kiến thức áp dụng
Khi nhân cả hai vế của BĐT với cùng một số c khác 0 ta được BĐT mới:
+ Cùng chiều với BĐT đã cho nếu c > 0
+ Ngược chiều với BĐT đã cho nếu c < 0.
Nếu a < b, c ≠ 0, thì ac < bc với c > 0; ac > bc với c < 0.
Khi cộng cùng một số vào cả hai vế của một bất đẳng thức ta được một bất đẳng thức mới cùng chiều với bất đẳng thức đã cho.
Nếu a < b thì a + c < b < c.
Câu 11:
Cho a < b, chứng minh:
a) 3a + 1 < 3b + 1 ; b) -2a – 5 > -2b - 5
Xem đáp án
a) Vì a < b
⇒ 3a < 3b (nhân hai vế với 3 > 0, BĐT không đổi chiều)
⇒ 3a + 1 < 3b + 1 (cộng hai vế với 1).
Vậy 3a + 1 < 3b + 1.
b) Vì a < b
⇒ -2a > -2b (nhân hai vế với -2 < 0, BĐT đổi chiều).
⇒ -2a – 5 > -2b – 5 (cộng hai vế với -5)
Vậy -2a – 5 > -2b – 5.
Kiến thức áp dụng
Khi nhân cả hai vế của BĐT với cùng một số c khác 0 ta được BĐT mới:
+ Cùng chiều với BĐT đã cho nếu c > 0
+ Ngược chiều với BĐT đã cho nếu c < 0.
Nếu a < b, c ≠ 0, thì ac < bc với c > 0; ac > bc với c < 0.
Khi cộng cùng một số vào cả hai vế của một bất đẳng thức ta được một bất đẳng thức mới cùng chiều với bất đẳng thức đã cho.
Nếu a < b thì a + c < b < c.
Câu 12:
Chứng minh:
a) 4.(-2) + 14 < 4.(-1) + 14
b) (-3).2 + 5 < (-3).(-5) + 5
Xem đáp án
a) Ta có: -2 < -1
⇒ 4.(-2) < 4.(-1) (nhân hai vế với 4 > 0, BĐT không đổi chiều).
⇒ 4.(-2) + 14 < 4.(-1) + 14 (cộng hai vế với 14)
Vậy 4.(-2) + 14 < 4.(-1) + 14.
b) Ta có: 2 > -5
⇒ (-3).2 < (-3).(-5) (nhân hai vế với -3 < 0, BĐT đổi chiều).
⇒ (-3).2 + 5 < (-3).(-5) + 5 (cộng hai vế với 5)
Vậy (-3).2 + 5 < (-3).(-5) + 5.
Kiến thức áp dụng
Khi nhân cả hai vế của BĐT với cùng một số c khác 0 ta được BĐT mới:
+ Cùng chiều với BĐT đã cho nếu c > 0
+ Ngược chiều với BĐT đã cho nếu c < 0.
Nếu a < b, c ≠ 0, thì ac < bc với c > 0; ac > bc với c < 0.
Khi cộng cùng một số vào cả hai vế của một bất đẳng thức ta được một bất đẳng thức mới cùng chiều với bất đẳng thức đã cho.
Nếu a < b thì a + c < b < c.
Câu 13:
So sánh a và b nếu:
a) a + 5 < b + 5; b) – 3a > -3b
c) 5a – 6 ≥ 5b – 6; d) -2a + 3 ≤ - 2b + 3
Xem đáp án
a) Từ a + 5 < b + 5
⇒ a + 5 + (-5) < b + 5 + (-5) (cộng hai vế với -5)
⇒ a < b
b) -3.a > -3.b
⇒ a < b (Nhân cả hai vế cho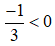 
< 0, BĐT đổi chiều).
c) 5a – 6 ≥ 5b – 6
⇒ 5a – 6 + 6 ≥ 5b – 6 + 6 (Cộng hai vế với 6)
⇒ 5a ≥ 5b
⇒ a ≥ b (Nhân cả hai vế cho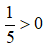 
> 0, BĐT không đổi chiều).
d) -2a + 3 ≤ - 2b + 3
⇒ -2a + 3 – 3 ≤ - 2b + 3 – 3 (Cộng cả hai vế với -3)
⇒ -2a ≤ - 2b
⇒ a ≥ b (Nhân cả hai vế cho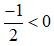 
< 0, BĐT đổi chiều).
Kiến thức áp dụng
Khi nhân cả hai vế của BĐT với cùng một số c khác 0 ta được BĐT mới:
+ Cùng chiều với BĐT đã cho nếu c > 0
+ Ngược chiều với BĐT đã cho nếu c < 0.
Nếu a < b, c ≠ 0, thì a : c < b : c với c > 0 ; a : c > b : c với c < 0.
Câu 14:
Cho a < b, hãy so sánh:
a) 2a +1 với 2b + 1
b) 2a +1 với 2b + 3
Xem đáp án
a) a < b
⇒ 2a < 2b (nhân hai vế với 2 > 0, BĐT không đổi chiều)
⇒ 2a + 1 < 2b + 1 (cộng hai vế với 1).
Vậy 2a + 1 < 2b + 1.
b) 1 < 3
⇒ 2b + 1 < 2b + 3 (Cộng hai vế với 2b)
Mà 2a + 1 < 2b + 1 (Theo ý a,)
⇒ 2a + 1 < 2b + 3 (Tính chất bắc cầu).
Vậy 2a + 1 < 2b + 3.
Kiến thức áp dụng
Khi nhân cả hai vế của BĐT với cùng một số c khác 0 ta được BĐT mới:
+ Cùng chiều với BĐT đã cho nếu c > 0
+ Ngược chiều với BĐT đã cho nếu c < 0.
Nếu a < b, c ≠ 0, thì ac < bc với c > 0; ac > bc với c < 0.
Khi cộng cùng một số vào cả hai vế của một bất đẳng thức ta được một bất đẳng thức mới cùng chiều với bất đẳng thức đã cho.
Nếu a < b thì a + c < b < c.
Tính chất bắc cầu: Nếu a < b và b < c thì a < c.