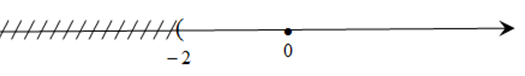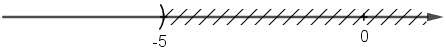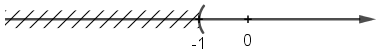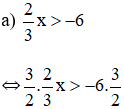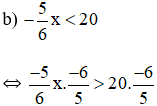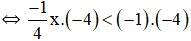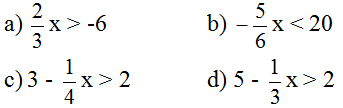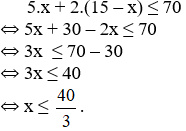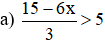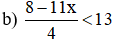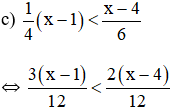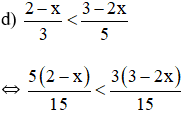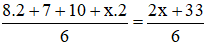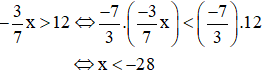Bài 4: Bất phương trình bậc nhất một ẩn
-
2553 lượt thi
-
22 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Trong các bất phương trình sau, hãy cho biết bất phương trình nào là bất phương trình bậc nhất một ẩn:
a) 2x – 3 < 0;
b) 0.x + 5 > 0;
c) 5x – 15 ≥ 0;
d) x2 > 0.
 Xem đáp án
Xem đáp án
- Bất phương trình a), c) là các bất phương trình bậc nhất một ẩn.
- Bất phương trình b) có a = 0 không thỏa mãn điều kiện a ≠ 0 nên không phải là bất phương trình bậc nhất một ẩn.
- Bất phương trình d) có mũ ở ẩn x là 2 nên không phải là bất phương trình bậc nhất một ẩn.
Câu 2:
Giải các bất phương trình sau:
a) x + 12 > 21;
b) -2x > -3x – 5.
 Xem đáp án
Xem đáp án
a) x + 12 > 21 ⇔ x > 21 - 12 ⇔ x > 9
Vậy tập nghiệm của bất phương trình x + 12 > 21 là {x|x > 9}
b) -2x > -3x – 5 ⇔ -2x + 3x > -5 ⇔ x > -5
Vậy tập nghiệm của bất phương trình -2x > -3x – 5 là {x|x > -5}
Câu 3:
Giải các bất phương trình sau (dùng quy tắc nhân):
a) 2x < 24;
b) -3x < 27.
 Xem đáp án
Xem đáp án
a) 2x < 24 ⇔ 2x.


⇔ x < 12
Vậy tập nghiệm của bất phương trình 2x < 24 là {x|x < 12}
b) -3x < 27 ⇔ -3x.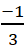
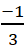
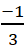
⇔ x > -9
Vậy tập nghiệm của bất phương trình - 3x < 27 là {x|x > -9}
Câu 4:
Giải thích sự tương đương:
a) x + 3 < 7 ⇔ x – 2 < 2;
b) 2x < - 4 ⇔ -3x > 6.
 Xem đáp án
Xem đáp án
a) x + 3 < 7 ⇔ x + 3 - 5 < 7-5 ( cộng -5 vào cả hai vế).
⇔ x – 2 < 2
b) 2x < -4 ⇔ 2x.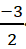
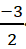
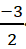
⇔ -3x > 6
Câu 5:
Giải bất phương trình - 4x – 8 < 0 và biểu diễn tập nghiệm trên trục số.
 Xem đáp án
Xem đáp án
-4x – 8 < 0 ⇔ -4x < 8
⇔ -4x : (- 4) > 8: (- 4) ⇔ x > -2
Vậy tập nghiệm của bất phương trình -4x – 8 < 0 là {x|x > -2}
Biểu diễn trên trục số
Câu 6:
Giải bất phương trình -0,2x – 0,2 > 0,4x – 2.
 Xem đáp án
Xem đáp án
-0,2x – 0,2 > 0,4x – 2
⇔ 0,4x – 2 < -0,2x – 0,2
⇔ 0,4x + 0,2x < -0,2 + 2
⇔ 0,6x < 1,8
⇔ 0,6x : 0,6 < 1,8: 0,6
⇔ x < 3
Vậy tập nghiệm của bất phương trình -0,2x – 0,2 > 0,4x – 2 là {x|x < 3}
Câu 7:
Giải các bất phương trình (theo quy tắc chuyển vế):
a) x - 5 > 3
b) x - 2x < -2x + 4
c) -3x > -4x + 2
d) 8x + 2 < 7x - 1
 Xem đáp án
Xem đáp án
(Áp dụng quy tắc: chuyển vế - đổi dấu)
a) x - 5 > 3
⇔ x > 3 + 5 (chuyển -5 từ vế trái sang vế phải và đổi dấu thành 5)
⇔ x > 8.
Vậy nghiệm của bất phương trình là x > 8.
b) x - 2x < -2x + 4
⇔ x - 2x + 2x < 4
⇔ x < 4
Vậy nghiệm của bất phương trình là x < 4.
c) -3x > -4x + 2
⇔ -3x + 4x > 2
⇔ x > 2
Vậy nghiệm của bất phương trình là x > 2.
d) 8x + 2 < 7x - 1
⇔ 8x - 7x < -1 - 2
⇔ x < -3
Vậy nghiệm của bất phương trình là x < -3.
Kiến thức áp dụng
+ Khi chuyển một hạng tử của bất phương trình từ vế này sang vế khác ta phải đổi dấu hạng tử đó và bất đẳng thức không đổi chiều.
Câu 8:
Giải các bất phương trình (theo quy tắc nhân):
a) 0,3x > 0,6 ;
b) -4x < 12;
c) -x > 4 ;
d) 1,5x > -9.
 Xem đáp án
Xem đáp án
a) 0,3x > 0,6
⇔ 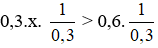
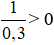
⇔ x > 2.
Vậy BPT có tập nghiệm x > 2.
b) -4x < 12
⇔ 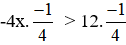
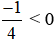
⇔ x > -3.
Vậy BPT có tập nghiệm x > -3.
c) –x > 4
⇔ (-x).(-1) < 4.(-1) (Nhân cả hai vế với -1 < 0, BĐT đổi chiều).
⇔ x < -4.
Vậy bất phương trình có tập nghiệm x < -4.
d) 1,5x > -9
⇔ 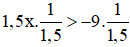
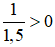
⇔ x > -6
Vậy bất phương trình có tập nghiệm x > -6
Kiến thức áp dụng
+ Ta có thể nhân hai vế của bất phương trình với cùng một số khác 0 và lưu ý:
Giữ nguyên chiều bất phương trình nếu số đó dương.
Đổi chiều bất phương trình nếu số đó âm.
+ Khi trình bày, không cần ghi câu giải thích.
Câu 9:
Giải thích sự tương đương sau:
a) x - 3 > 1 ⇔ x + 3 > 7
b) -x < 2 ⇔ 3x > -6
 Xem đáp án
Xem đáp án
a) x – 3 > 1
⇔ x – 3 + 6 > 1 + 6 (Cộng 6 vào cả hai vế).
Hay x + 3 > 7..
Vậy hai bpt trên tương đương.
b) –x < 2
⇔ (-x).(-3) > 2.(-3) (Nhân cả hai vế với -3 < 0, BPT đổi dấu)
⇔ 3x > -6.
Vậy hai BPT trên tương đương.
Kiến thức áp dụng
Ta có thể thu được bất phương trình tương đương với bpt ban đầu khi cùng cộng cả hai vế với một số hoặc cùng nhân cả hai vế với một số khác 0 (đổi chiều nếu số đó dương).
Câu 10:
Giải các bất phương trình và biểu diễn tập nghiệm trên trục số:
a) 1,2x < -6 ; b) 3x + 4 > 2x + 3
 Xem đáp án
Xem đáp án
a) 1,2x < -6
⇔1,2 x : 1,2 < -6 : 1,2
⇔ x < - 5
Vậy nghiệm của bất phương trình là x < -5.
b) 3x + 4 > 2x + 3
⇔ 3x - 2x > 3 - 4 (chuyển vế 2x và 4, đổi dấu hạng tử).
⇔ x > -1
Vậy nghiệm của bất phương trình là x > -1.
Kiến thức áp dụng
+ Ta có thể nhân hai vế của bất phương trình với cùng một số khác 0 và lưu ý:
Giữ nguyên chiều bất phương trình nếu số đó dương.
Đổi chiều bất phương trình nếu số đó âm.
+ Khi trình bày, không cần ghi câu giải thích.
Câu 11:
Giải các bất phương trình và biểu diễn tập nghiệm trên trục số:
a) 2x - 3 > 0 ; b) 3x + 4 < 0
c) 4 - 3x ≤ 0 ; d) 5 - 2x ≥ 0
 Xem đáp án
Xem đáp án
a) 2x – 3 > 0
⇔ 2x > 3 (Chuyển vế -3).
⇔ 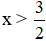
Vậy BPT có nghiệm
b) 3x + 4 < 0
⇔ 3x < -4 (chuyển vế 4).
⇔ 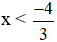
Vậy BPT có tập nghiệm
c) 4 – 3x ≤ 0
⇔ -3x ≤ -4 (Chuyển vế hạng tử 4).
⇔ 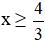
Vậy BPT có tập nghiệm
d) 5 – 2x ≥ 0
⇔ -2x ≥ -5 (Chuyển vế hạng tử 5).
⇔ 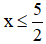
Vậy BPT có nghiệm
Kiến thức áp dụng
+ Ta có thể nhân hai vế của bất phương trình với cùng một số khác 0 và lưu ý:
Giữ nguyên chiều bất phương trình nếu số đó dương.
Đổi chiều bất phương trình nếu số đó âm.
+ Khi trình bày, không cần ghi câu giải thích.
Câu 12:
Giải các bất phương trình:
a) 2x - 1 > 5 ; b) 3x - 2 < 4
c) 2 - 5x ≤ 17 ; d) 3 - 4x ≥ 19
 Xem đáp án
Xem đáp án
a) 2x - 1 > 5
⇔ 2x > 1 + 5 (Chuyển vế và đổi dấu hạng tử -1)
⇔ 2x > 6
⇔ x > 3 (Chia cả hai vế cho 2 > 0, BPT không đổi chiều).
Vậy nghiệm của bất phương trình là x > 3.
b) 3x - 2 < 4
⇔ 3x < 4 + 2 (Chuyển vế và đổi dấu hạng tử -2)
⇔ 3x < 6
⇔ x < 2 (Chia cả hai vế cho 3 > 0, BPT không đổi chiều).
Vậy nghiệm của bất phương trình là x < 2.
c) 2 - 5x ≤ 17
⇔ -5x ≤ 17 - 2 (Chuyển vế và đổi dấu hạng tử 2)
⇔ -5x ≤ 15
⇔ x ≥ -3 (Chia cả hai vế cho -5 < 0, BPT đổi chiều).
Vậy nghiệm của bất phương trình là x ≥ - 3
d) 3 - 4x ≥ 19
⇔ -4x ≥ 19 - 3 (Chuyển vế và đổi dấu hạng tử 3)
⇔ -4x ≥ 16
⇔ x ≤ -4 (Chia cả hai vế cho -4 < 0, BPT đổi chiều).
Vậy nghiệm của bất phương trình là x ≤ -4
Kiến thức áp dụng
+ Ta có thể nhân hai vế của bất phương trình với cùng một số khác 0 và lưu ý:
Giữ nguyên chiều bất phương trình nếu số đó dương.
Đổi chiều bất phương trình nếu số đó âm.
+ Ta có thể một hạng tử từ vế này sang vế khác và phải đổi dấu hạng tử đó.
+ Khi trình bày, không cần ghi câu giải thích.
Câu 13:
Giải các bất phương trình:
 Xem đáp án
Xem đáp án
(Nhân cả hai vế với 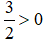
⇔ x > -9.
Vậy bất phương trình có nghiệm x > -9.
(Nhân cả hai vế với 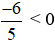
⇔ x > -24
Vậy bất phương trình có nghiệm x > -24.
(Nhân cả hai vế với -4 < 0, BPT đổi chiều).
⇔ x < 4.
Vậy BPT có nghiệm x < 4.
(Nhân cả hai vế với -3 < 0, BPT đổi chiều)
⇔ x < 9.
Vậy BPT có nghiệm x < 9.
Kiến thức áp dụng
+ Ta có thể nhân hai vế của bất phương trình với cùng một số khác 0 và lưu ý:
Giữ nguyên chiều bất phương trình nếu số đó dương.
Đổi chiều bất phương trình nếu số đó âm.
+ Ta có thể một hạng tử từ vế này sang vế khác và phải đổi dấu hạng tử đó.
+ Khi trình bày, không cần ghi câu giải thích.
Câu 14:
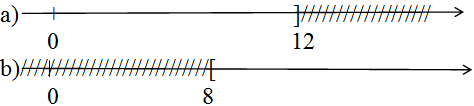
Hình vẽ sau biểu diễn tập nghiệm của bất phương trình nào? (Kể ba bất phương trình có cùng tập nghiệm).
 Xem đáp án
Xem đáp án
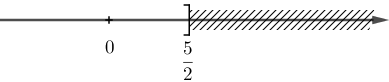
a) Hình a) biểu diễn tập nghiệm của bất phương trình:
x ≤ 12 hoặc x + 4 ≤ 16 hoặc 2x + 1 ≤ 25
b) Hình biểu diễn tập nghiệm của bất phương trình:
x ≥ 8 hoặc x + 3 ≥ 11 hoặc 3 – 2x ≤ -13.
Câu 15:
Đố: Kiểm tra xem giá trị x = -2 có là nghiệm của bất phương trình sau không?
a) x + 2x2 – 3x3 + 4x4 – 5 < 2x2 – 3x3 + 4x4 – 6;
b) (-0,001)x > 0,003.
 Xem đáp án
Xem đáp án
a) x + 2x2 - 3x3 + 4x4 - 5 < 2x2 - 3x3 + 4x4 - 6
⇔ x < 2x2 - 3x3 + 4x4 - 6 - 2x2 + 3x3 - 4x4 + 5 (chuyển vế - đổi dấu)
⇔ x < -1 (*)
Vì -2 < -1 nên -2 là nghiệm của bất phương trình
Vậy x = -2 là nghiệm của bất phương trình.
b) (-0,001)x > 0,003
⇔ x < -3 (chia cả hai vế cho -0,001)
Vì -2 > -3 nên -2 không phải nghiệm của bất phương trình
Vậy x = -2 không là nghiệm của bất phương trình.
Kiến thức áp dụng
+ Ta có thể nhân hai vế của bất phương trình với cùng một số khác 0 và lưu ý:
Giữ nguyên chiều bất phương trình nếu số đó dương.
Đổi chiều bất phương trình nếu số đó âm.
+ Ta có thể một hạng tử từ vế này sang vế khác và phải đổi dấu hạng tử đó.
Câu 16:
Cho bất phương trình x2 > 0.
a) Chứng tỏ x = 2, x = -3 là nghiệm của bất phương trình đã cho.
b) Có phải mọi giá trị của ẩn x đều là nghiệm của bất phương trình đã cho hay không?
 Xem đáp án
Xem đáp án
a) Thay x = 2 vào bất phương trình ta được: x2 = 22 = 4 > 0
Vậy x = 2 là một nghiệm của bất phương trình x2 > 0.
Thay x = -3 vào bất phương trình ta được x2 = (-3)2 = 9 > 0
Vậy x = -3 là một nghiệm của bất phương trình x2 > 0.
b) Với x = 0 ta có x2 = 02 = 0
⇒ x = 0 không phải nghiệm của bất phương trình x2 > 0.
Vậy không phải mọi giá trị của ẩn x đều là nghiệm của bất phương trình đã cho.
Câu 17:
Tìm x sao cho:
a) Giá trị của biểu thức 2x - 5 không âm.
b) Giá trị của biểu thức -3x không lớn hơn giá trị của biểu thức -7x + 5.
Lưu ý:
- không âm tức là ≥ 0
- không lớn hơn tức là ≤
 Xem đáp án
Xem đáp án
a) Để giá trị biểu thức 2x – 5 không âm
⇔ 2x – 5 ≥ 0.
⇔ 2x ≥ 5 (Chuyển vế và đổi dấu hạng tử -5).
⇔ 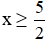
Vậy với 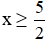
b) Để giá trị của biểu thức -3x không lớn hơn giá trị của biểu thức -7x + 5
⇔ -3x ≤ -7x + 5 (Chuyển vế và đổi dấu hạng tử -7x)
⇔ -3x + 7x ≤ 5
⇔ 4x ≤ 5
⇔
Vậy với 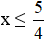
Kiến thức áp dụng
+ Biểu thức A dương ⇔ A > 0
+ Biểu thức A không âm ⇔ A ≥ 0.
Câu 18:
Một người có số tiền không quá 70000 đồng gồm 15 tờ giấy bạc với hai loại mệnh giá: loại 2000 đồng và loại 5000 đồng. Hỏi người đó có bao nhiêu tờ giấy bạc loại 5000 đồng?
 Xem đáp án
Xem đáp án
Gọi x là số tờ giấy bạc loại 5 000 đồng người đó có (0 < x < 15 , x ∈ N).
Vì tổng số tờ 2 000 đồng và 5 000 đồng là 15 tờ nên ta có điều kiện x < 15
và số tờ 2 000 đồng người đó có là: 15 – x (tờ)
⇒ Tổng số tiền người đó có là: 5.x + 2.(15 – x) (nghìn đồng).
Theo bài ra, người đó có số tiền không quá 70 nghìn đồng nên ta có bất phương trình:
Kết hợp với điều kiện nên x có thể nhận một trong các giá trị {1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 13}
Câu 19:
Giải các bất phương trình và biểu diễn tập nghiệm trên trục số:
 Xem đáp án
Xem đáp án
⇔ 15 – 6x > 15 (Nhân cả hai vế với 3 > 0, BPT không đổi chiều)
⇔ -6x > 15 – 15 (Chuyển vế và đổi dấu hạng tử 15)
⇔ -6x > 0
⇔ x < 0 (Chia cả hai vế với -6 < 0, BPT đổi chiều)
Vậy nghiệm của bất phương trình là x < 0.
⇔ 8 – 11x < 13.4 (Nhân cả hai vế với 4 > 0, BPT không đổi chiều)
⇔ 8 – 11x < 52
⇔ -11x < 52 – 8 (Chuyển vế và đổi dấu hạng tử 8)
⇔ -11x < 44
⇔ x > 44 : (-11) (Chia cả hai vế cho -11 < 0, BPT đổi chiều
⇔ x > -4.
Vậy bất phương trình có nghiệm x > -4.
⇔ 3(x – 1) < 2(x – 4) (Nhân cả hai vế với 12 > 0, BPT không đổi chiều)
⇔ 3x – 3 < 2x – 8
⇔ 3x – 2x < -8 + 3 (Chuyển vế và đổi dấu 2x và -3)
⇔ x < -5
Vậy bất phương trình có tập nghiệm x < -5.
⇔ 5(2 – x) < 3(3 – 2x) (Nhân cả hai vế với 15 > 0, BPT không đổi chiều)
⇔ 10 – 5x < 9 – 6x
⇔ 6x – 5x < 9 – 10 (Chuyển vế và đổi dấu -6x và 10)
⇔ x < -1.
Vậy bất phương trình có tập nghiệm x < -1.
Kiến thức áp dụng
+ Ta có thể nhân hai vế của bất phương trình với cùng một số khác 0 và lưu ý:
Giữ nguyên chiều bất phương trình nếu số đó dương.
Đổi chiều bất phương trình nếu số đó âm.
+ Ta có thể một hạng tử từ vế này sang vế khác và phải đổi dấu hạng tử đó.
+ Khi trình bày, không cần ghi câu giải thích.
Câu 20:
Giải các bất phương trình:
a) 8x + 3(x + 1) > 5x - (2x - 6)
b) 2x(6x - 1) > (3x - 2)(4x + 3)
 Xem đáp án
Xem đáp án
a) 8x + 3(x + 1) > 5x – (2x – 6)
⇔ 8x + 3x + 3 > 5x – 2x + 6
⇔ 8x + 3x – 5x + 2x > 6 – 3 (Chuyển vế, đổi dấu)
⇔ 8x > 3
⇔ 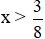
Vậy bất phương trình có nghiệm
b) 2x(6x – 1) > (3x – 2)(4x + 3)
⇔ 12x2 – 2x > 12x2 – 8x + 9x – 6
⇔ 12x2 – 2x – 12x2 + 8x – 9x > -6 (Chuyển vế, đổi dấu)
⇔ -3x > -6
⇔ x < 2 (Chia cả hai vế cho -3 < 0, BPT đổi chiều)
Vậy bất phương trình có nghiệm x < 2.
Kiến thức áp dụng
+ Ta có thể nhân hai vế của bất phương trình với cùng một số khác 0 và lưu ý:
Giữ nguyên chiều bất phương trình nếu số đó dương.
Đổi chiều bất phương trình nếu số đó âm.
+ Ta có thể một hạng tử từ vế này sang vế khác và phải đổi dấu hạng tử đó.
+ Khi trình bày không cần giải thích.
Câu 21:
Đố: Trong một kì thi, bạn Chiến phải thi bốn môn Văn, Toán, Tiếng Anh và Hóa. Chiến đã thi ba môn và được kết quả như bảng sau:
| Môn | Văn | Tiếng Anh | Hóa |
| Điểm | 8 | 7 | 10 |
Kỳ thi quy định muốn đạt loại giỏi phải có điểm trung bình các môn thi là 8 trở lên và không có môn nào bị điểm dưới 6. Biết môn Văn và Toán được tính hệ số 2. Hãy cho biết, để đạt loại giỏi bạn Chiến phải có điểm thi môn Toán ít nhất là bao nhiêu điểm?
 Xem đáp án
Xem đáp án
Gọi x là điểm thi môn Toán (x ≤ 10).
Vì môn Văn và Toán được tính hệ số 2 nên ta có điểm trung bình của Chiến là:
Theo đề bài, để đạt loại Giỏi thì điểm môn Toán của Chiến phải thỏa mãn điều kiện: x ≥ 6 (1) và 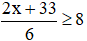
Xét (2): 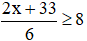
Kết hợp với (1) ta được: x ≥ 7,5.
Vậy để đạt được loại giỏi thì bạn Chiến phải có điểm thi môn Toán thấp nhất là 7,5 điểm.
Câu 22:
Đố: Tìm sai lầm trong các "lời giải" sau:
a) Giải bất phương trình -2x > 23. Ta có:
-2x > 23 ⇔ x > 23 + 2 ⇔ x > 25.
Vậy nghiệm của bất phương trình là x > 25.
b) Giải bất phương trình . Ta có:
 Xem đáp án
Xem đáp án
a) Sai lầm là coi -2 là hạng từ và chuyển vế hạng tử này trong khi -2 là một nhân tử.
Lời giải đúng:
-2x > 23
⇔ x < 23 : (-2) (chia cho số âm nên đổi chiều)
⇔ x < -11,5
Vậy nghiệm của bất phương trình là x < -11,5
b) Sai lầm là nhân hai vế của bất phương trình với 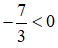
Lời giải đúng:
Vậy nghiệm của bất phương trình là x < -28