Bài 5: Phương trình chứa dấu giá trị tuyệt đối
-
2276 lượt thi
-
5 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Rút gọn các biểu thức:
a) C = |-3x| + 7x – 4 khi x ≤ 0;
b) D = 5 – 4x + |x - 6| khi x < 6.
Xem đáp án
a) x ≤ 0 nên – 3x ≥ 0 ⇒ |-3x| = -3x
Vậy C = |-3x| + 7x – 4 = -3x + 7x - 4 = 4x - 4
b) x < 6 nên x – 6 < 0 ⇒ |x - 6| = -(x - 6) = 6 - x
Vậy D = 5 – 4x + |x - 6| = 5 – 4x + 6 – x = 11 – 5x
Câu 2:
Giải các phương trình:
a) |x + 5| = 3x + 1;
b) |-5x| = 2x + 21.
Xem đáp án
a)
+) Ta có: | x+ 5| = x + 5 khi x+ 5 ≥ 0 hay x ≥ -5
| x+ 5| = - (x + 5) khi x+ 5 < 0 hay x < - 5
Vậy để giải phương trình đã cho ta quy về giải hai phương trình:
+) Phương trình: x + 5 = 3x + 1 với điều kiện x ≥ -5
Ta có: x + 5 = 3x + 1
⇔ - 2x = - 4 ⇔ x = 2 (thỏa mãn điều kiện x ≥ -5)
+)Phương trình: - (x + 5) = 3x + 1 với điều kiện x < -5
Ta có: -x - 5 = 3x + 1 ⇔ - 4x = 6
⇔ x = 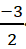(không thỏa mãn điều kiện x < -5)
Vậy tập nghiệm của bất phương trình |x + 5| = 3x + 1 là S = {2}
b)
+) Ta có: |- 5x| = - 5x khi -5x ≥ 0 hay x ≤ 0
| - 5x| = 5x khi – 5x < 0 hay x > 0
Vậy để giải phương trình đã cho ta quy về giải hai phương trình:
+) Phương trình: - 5x = 2x + 21 với điều kiện x ≥ 0
⇔ - 7x = 21 ⇔ x = - 3 ( thỏa mãn điều kiện x ≤ 0 )
+) Phương trình: 5x = 2x + 21 với điều kiện x> 0
⇔ 3x = 21
⇔ x = 7 (thỏa mãn điều kiện x > 0)
Vậy tập nghiệm của bất phương trình |-5x|= 2x + 21 là S = {-3; 7}.
Câu 3:
Bỏ dấu giá trị tuyệt đối và rút gọn các biểu thức:
a) A = 3x + 2 + |5x| trong hai trường hợp: x ≥ 0 và x < 0;
b) B = |-4x| - 2x + 12 trong hai trường hợp: x ≤ 0 và x > 0;
c) C = |x - 4| - 2x + 12 khi x > 5;
d) D = 3x + 2 + |x + 5|.
Xem đáp án
a) - Khi x ≥ 0 ta có 5x ≥ 0 nên |5x| = 5x
Vậy A = 3x + 2 + 5x = 8x + 2
- Khi x < 0 ta có 5x < 0 nên |5x| = -5x
Vậy A = 3x + 2 - 5x = -2x + 2
b) - Khi x ≤ 0 ta có -4x ≥ 0 (nhân hai vế với số âm) nên |-4x| = -4x
Vậy B = -4x - 2x + 12 = -6x + 12
- Khi x > 0 ta có -4x < 0 nên |-4x| = -(-4x) = 4x
Vậy B = 4x - 2x + 12 = 2x + 12
c) - Khi x > 5 ta có x - 4 > 1 (trừ hai vế cho 4) hay x - 4 > 0 nên |x - 4| = x - 4
Vậy C = x - 4 - 2x + 12 = -x + 8
d) Ta có: |x + 5| = x + 5 khi x + 5 ≥ 0 hay x ≥ -5.
|x + 5| = -(x + 5) khi x + 5 < 0 hay x < -5.
Vậy :
+ Với x ≥ -5 thì D = 3x + 2 + x + 5 = 4x + 7.
+ Với x < -5 thì D = 3x + 2 – (x + 5) = 3x + 2 – x – 5 = 2x – 3.
Kiến thức áp dụng
+ Giá trị tuyệt đối của A, kí hiệu là |A|:
|A| = A nếu A ≥ 0
|A| = -A nếu A < 0.
Câu 4:
Giải các phương trình:
a) |2x| = x - 6 ; b) |-3x| = x - 8
c) |4x| = 2x + 12 ; d) |-5x| - 16 = 3x
Xem đáp án
a) |2x| = x – 6 (1)
Ta có: |2x| = 2x khi 2x ≥ 0 hay x ≥ 0
|2x| = -2x khi 2x < 0 hay x < 0.
Vậy phương trình (1) tương đương với:
+ 2x = x – 6 với điều kiện x ≥ 0
2x = x – 6 ⇔ x = -6
Giá trị x = -6 không thỏa mãn điều kiện x ≥ 0 nên không phải nghiệm của (1)
+ -2x = x – 6 với điều kiện x < 0
-2x = x – 6 ⇔ -3x = -6 ⇔ x = 2.
Giá trị x = 2 không thỏa mãn điều kiện x < 0 nên không phải nghiệm của (1).
Vậy phương trình (1) vô nghiệm.
b) |-3x| = x – 8 (2)
Ta có: |-3x| = -3x khi -3x ≥ 0 hay x ≤ 0.
|-3x| = -(-3x) = 3x khi -3x < 0 hay x > 0.
Vậy phương trình (2) tương đương với:
+ -3x = x – 8 với điều kiện x ≤ 0
-3x = x – 8 ⇔ -4x = -8 ⇔ x = 2
Giá trị x = 2 không thỏa mãn điều kiện x ≤ 0 nên không phải nghiệm của (2).
+ 3x = x – 8 với điều kiện x > 0
3x = x – 8 ⇔ 2x = -8 ⇔ x = -4.
Giá trị x = -4 không thỏa mãn điều kiện x > 0 nên không phải nghiệm của (2).
Vậy phương trình (2) vô nghiệm.
c) |4x| = 2x + 12 (3)
Ta có: |4x| = 4x khi 4x ≥ 0 ⇔ x ≥ 0
|4x| = -4x khi 4x < 0 hay x < 0.
Vậy phương trình (3) tương đương với:
+ 4x = 2x + 12 với điều kiện x ≥ 0
4x = 2x + 12 ⇔ 2x = 12 ⇔ x = 6.
Giá trị x = 6 thỏa mãn điều kiện x ≥ 0 nên là nghiệm của (3)
+ -4x = 2x + 12 với điều kiện x < 0
-4x = 2x + 12 ⇔ -6x = 12 ⇔ x = -2.
Giá trị x = -2 thỏa mãn điều kiện x < 0 nên là nghiệm của (3).
Vậy phương trình (3) có hai nghiệm x = 6 và x = -2.
d) |-5x| - 16 = 3x (4)
Ta có: |-5x| = -5x khi -5x ≥ 0 hay x ≤ 0.
|-5x| = -(-5x) = 5x khi -5x < 0 hay x > 0.
Vậy phương trình (4) tương đương với:
+ -5x – 16 = 3x với điều kiện x ≤ 0.
-5x – 16 = 3x ⇔ -5x – 3x = 16 ⇔ -8x = 16 ⇔ x = -2.
Giá trị x = -2 thỏa mãn điều kiện x ≤ 0 nên là nghiệm của (4).
+ 5x – 16 = 3x với điều kiện x > 0.
5x – 16 = 3x ⇔ 5x – 3x = 16 ⇔ 2x = 16 ⇔ x = 8
Giá trị x = 8 thỏa mãn điều kiện x > 0 nên là nghiệm của (4).
Vậy phương trình (4) có nghiệm x = -2 và x = 8.
Kiến thức áp dụng
+ Giá trị tuyệt đối của A, kí hiệu là |A|:
|A| = A nếu A ≥ 0
|A| = -A nếu A < 0.
Câu 5:
Giải các phương trình:
a) |x - 7| = 2x + 3 ; b) |x + 4| = 2x - 5
c) |x+ 3| = 3x - 1 ; d) |x - 4| + 3x = 5
Xem đáp án
a) |x – 7| = 2x + 3 (1)
Ta có: |x – 7| = x – 7 khi x – 7 ≥ 0 hay x ≥ 7.
|x – 7| = -(x – 7) = 7 – x khi x – 7 < 0 hay x < 7.
Vậy phương trình (1) tương đương với:
+ x – 7 = 2x + 3 khi x ≥ 7
x – 7 = 2x + 3 ⇔ x = -10.
Giá trị x = -10 không thỏa mãn điều kiện x ≥ 7 nên không phải nghiệm của (1).
+ 7 – x = 2x + 3 khi x < 7.
7 – x = 2x + 3 ⇔ 3x = 4 ⇔ x = 4/3
Giá trị x = 4/3 thỏa mãn điều kiện x < 7 nên là nghiệm của (1)
Vậy phương trình (1) có nghiệm x = 4/3.
b) |x + 4| = 2x – 5 (2)
Ta có: |x + 4| = x + 4 khi x + 4 ≥ 0 hay x ≥ -4.
|x + 4| = -(x + 4) = -x – 4 khi x + 4 < 0 hay x < -4.
Vậy phương trình (1) tương đương với:
+ x + 4 = 2x – 5 khi x ≥ -4
x + 4 = 2x – 5 ⇔ x = 9
Giá trị x = 9 thỏa mãn điều kiện x ≥ -4 nên là nghiệm của (2).
+ -x – 4 = 2x – 5 khi x < -4.
– x – 4 = 2x – 5 ⇔ 3x = 1 ⇔ x = 1/3
Giá trị x = 1/3 không thỏa mãn điều kiện x < -4 nên không phải nghiệm của (2)
Vậy phương trình (2) có nghiệm x = 9.
c) |x + 3| = 3x – 1 (3)
Ta có : |x + 3| = x + 3 khi x + 3 ≥ 0 hay x ≥ -3.
|x + 3| = -(x + 3) = -x – 3 khi x + 3 < 0 hay x < -3.
Vậy phương trình (3) tương đương với:
+ x + 3 = 3x – 1 với điều kiện x ≥ -3
x + 3 = 3x – 1 ⇔ 2x = 4 ⇔ x = 2.
Giá trị x = 2 thỏa mãn điều kiện x ≥ -3 nên là nghiệm của phương trình (3).
+ -x – 3 = 3x – 1 với điều kiện x < -3
-x – 3 = 3x – 1 ⇔ 4x = -2 ⇔ x = -1/2.
Giá trị x = -1/2 không thỏa mãn điều kiện x < -3 nên không phải nghiệm của (3).
Vậy phương trình có nghiệm x = 2.
d) |x – 4| + 3x = 5 (4)
+) Ta có: |x - 4| = x – 4 nếu hay x ≥ 4
| x- 4| = - (x – 4) = 4 - x nếu x - 4 < 0 hay x < 4
Vậy để giải phương trình (4) ta quy về giải hai phương trình
+) Phương trình: x - 4 + 3x = 5 với x ≥ 4
Ta có: x- 4 + 3x = 5 ⇔ 4x = 9 ⇔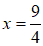 
( không thỏa mãn điều kiện x ≥ 4 nên không là nghiệm của phương trình (4).
+) Phương trình: 4 – x + 3x = 5 với x< 4
Ta có: 4 – x + 3x = 5 ⇔ 4 + 2x = 5 ⇔ 2x = 1 ⇔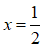 
(thỏa mãn điều kiện x < 4).
Vậy phương trình có nghiệm .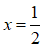
Kiến thức áp dụng
+ Giá trị tuyệt đối của A, kí hiệu là |A|:
|A| = A nếu A ≥ 0
|A| = -A nếu A < 0.
Vậy phương trình có nghiệm x = 1/2