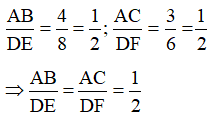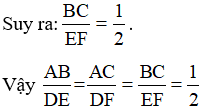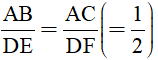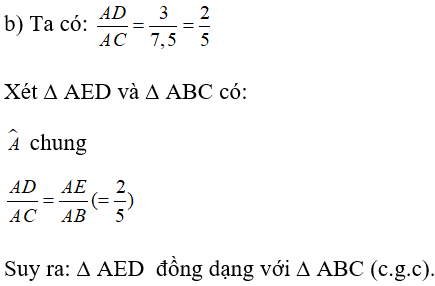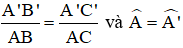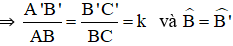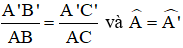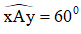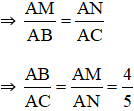Bài 6: Trường hợp đồng dạng thứ hai
-
3517 lượt thi
-
6 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
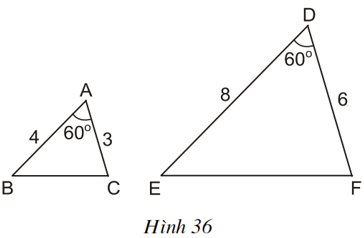
Cho hai tam giác ABC và DEF có kích thước như trong hình 36.
- So sánh các tỉ số
- Đo các đoạn thẳng BC, EF. Tính tỉ số , so sánh với các tỉ số trên và dự đoán sự đồng dạng của hai tam giác ABC và DEF.
 Xem đáp án
Xem đáp án
Đo các cạnh ta có: BC ≈ 3,6 cm; EF ≈ 7,2 cm
Dự đoán : ΔABC ∼ ΔDEF
Câu 2:
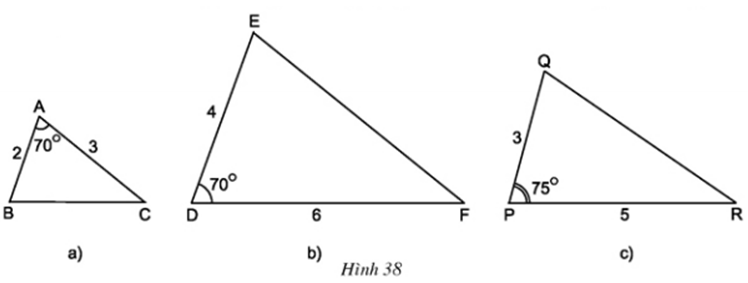
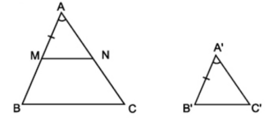
Hãy chỉ ra các cặp tam giác đồng dạng với nhau từ các tam giác sau đây (h.38):
 Xem đáp án
Xem đáp án
Xét ΔABC và ΔDEF có:
∠A = ∠D = 70o
⇒ ΔABC 
Câu 3:
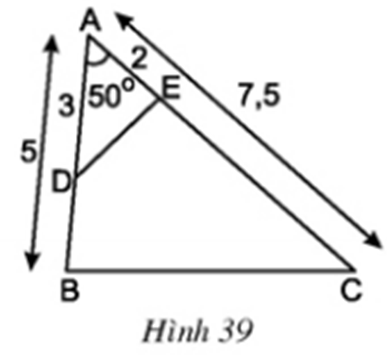
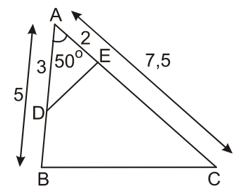
a) Vẽ tam giác ABC có = 50o, AB = 5cm, AC = 7,5cm (h.39)
b) Lấy trên các cạnh AB, AC lần lượt hai điểm D, E sao cho AD = 3cm, AE = 2cm. Hai tam giác AED và ABC có đồng dạng với nhau không ? Vì sao ?
 Xem đáp án
Xem đáp án
a) Cách vẽ:
Bước 1. Vẽ đoạn thẳng AB = 5cm.
Bước 2. Vẽ góc BAx bằng 50o, trên tia Ax lấy điểm C sao cho AC = 7,5 cm.
Bước 3. Nối B với C ta được tam giác ABC thỏa mãn yêu cầu bài toán.
Câu 4:
Trên một cạnh của góc xOy ( ≠ 180o), đặt các đoạn thẳng OA = 5cm, OB = 16cm. Trên cạnh thứ hai của góc đó, đặt các đoạn thẳng OC = 8cm, OD = 10cm.
a) Chứng minh hai tam giác OCB và OAD đồng dạng.
b) Gọi giao điểm của các cạnh AD và BC là I, chứng minh rằng hai tam giác IAB và ICD có các góc bằng nhau từng đôi một.
 Xem đáp án
Xem đáp án
Kiến thức áp dụng
+ Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau thì hai tam giác đó đồng dạng.
ΔABC và ΔA’B’C’ có:
⇒ ΔABC 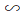
+ Định lí tổng ba góc: Trong một tam giác, tổng của ba góc trong luôn bằng 180º.
Câu 5:
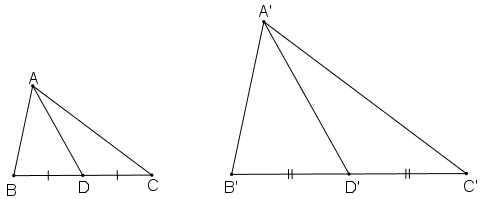
Chứng minh rằng nếu tam giác A'B'C' đồng dạng với tam giác ABC theo tỉ số k, thì tỉ số của hai đường trung tuyến tương ứng của hai tam giác đó cũng bằng k.
 Xem đáp án
Xem đáp án
Giả sử ΔA’B’C’ 
Gọi D, D’ lần lượt là trung điểm BC và B’C’.

Kiến thức áp dụng
+ Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau thì hai tam giác đó đồng dạng.
ΔABC và ΔA’B’C’ có:
⇒ ΔABC 
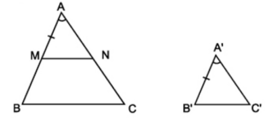
Câu 6:
Dựng tam giác ABC, biết = 60º; tỉ số và đường cao AH = 6cm.
 Xem đáp án
Xem đáp án
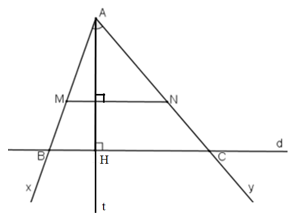
* Cách dựng:
+ Dựng góc
+ Trên tia Ax lấy điểm M sao cho AM = 4; trên tia Ay lấy điểm N sao cho AN = 5.
+ Kẻ tia At vuông góc với MN
+ Trên tia At lấy điểm H sao cho AH = 6cm.
+ Kẻ đường thẳng d qua H và vuông góc với At cắt Ax và Ay lần lượt tại B và C.
Ta được tam giác ABC cần dựng.
* Chứng minh :
Áp dụng định lí: Một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại tạo thành một tam giác đồng dạng với tam giác đã cho.
ΔABC dựng được có AH ⊥ BC ; AH = 6 và 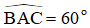 ;
;
Lại có AH ⊥ BC, MN ⊥ AH ⇒ MN // BC
⇒ ΔAMN 
Suy ra:
(tính chất hai tam giác đồng dạng).
Vậy tam giác ABC dựng được thỏa mãn yêu cầu đề bài.