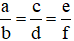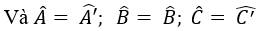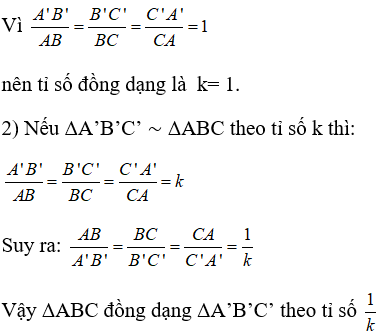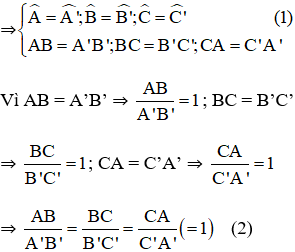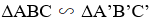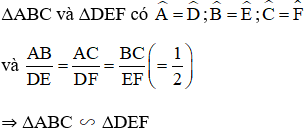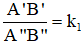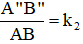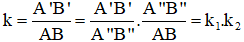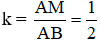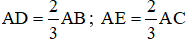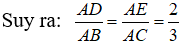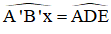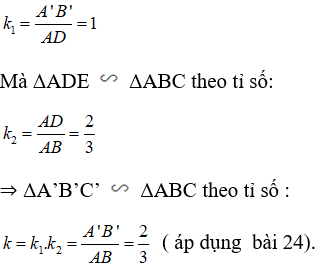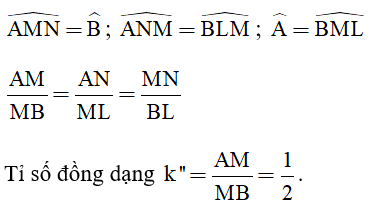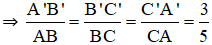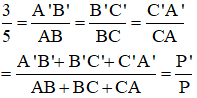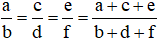Bài 4: Khái niệm hai tam giác đồng dạng
-
3514 lượt thi
-
8 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
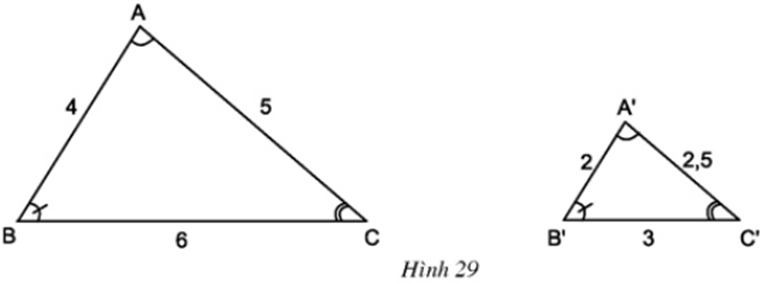
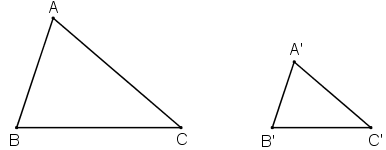
Cho hai tam giác ABC và A’B’C’ (h.29)
Nhìn vào hình vẽ hãy viết các cặp góc bằng nhau.
Tính các tỉ số rồi so sánh các tỉ số đó.
Xem đáp án
Các cặp góc bằng nhau:
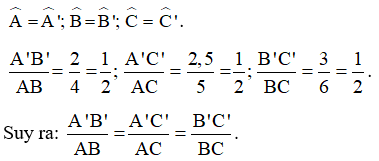
Câu 2:
1) Nếu ΔA’B’C’ = ΔABC thì tam giác A’B’C’ có đồng dạng với tam giác ABC không ? Tỉ số đồng dạng là bao nhiêu ?
2) Nếu ΔA’B’C’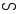 
ΔABC theo tỉ số k thì ΔABC 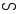ΔA’B’C’ theo tỉ số nào ?
Xem đáp án
1) Nếu Δ ABC = Δ A’B’C’ ta suy ra:
AB= A’B’, AC= A’C’, BC = B’C’
Theo định nghĩa hai tam giác đồng dạng, suy ra hai tam giác ABC và A’B’C’ đồng dạng với nhau
Câu 3:
Trong hai mệnh đề sau đây, mệnh đề nào đúng? Mệnh đề nào sai?
a) Hai tam giác bằng nhau thì đồng dạng với nhau.
b) Hai tam giác đồng dạng với nhau thì bằng nhau.
Xem đáp án
a) Mệnh đề Đúng.
Giả sử có ΔABC = ΔA’B’C’
Từ (1) và (2) suy ra 
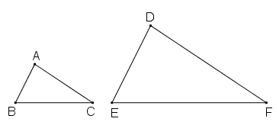
b) Mệnh đề Sai.
nhưng ΔABC và ΔDEF không bằng nhau
Kiến thức áp dụng
Hai tam giác ABC và A’B’C’ được gọi là đồng dạng nếu:
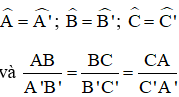
Câu 4:
ΔA'B'C' 
ΔA''B''C'' theo tỉ số đồng dạng k1, ΔA''B''C'' ΔABC theo tỉ số đồng dạng k2. Hỏi tam giác A'B'C' đồng dạng với tam giác ABC theo tỉ số nào?
Xem đáp án
ΔA'B'C' ΔA''B''C'' theo tỉ số đồng dạng k1 ⇒ 
ΔA''B''C'' ΔABC theo tỉ số đồng dạng k2 ⇒ 
Mà ΔA'B'C' ΔA''B''C''; ΔA''B''C'' ΔABC
⇒ ΔA'B'C' ΔABC (theo tính chất 3)
Tỉ số đồng dạng:
Vậy tam giác A'B'C' đồng dạng với tam giác ABC theo tỉ số k1.k2.
Kiến thức áp dụng
+ ΔABC ΔA’B’C’.
Tỉ số đồng dạng là tỉ số giữa các cạnh tương ứng:
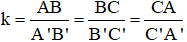
+ Nếu ΔA'B'C' ΔA''B''C'' và ΔA''B''C'' ΔABC
⇒ ΔA'B'C' ΔABC
Câu 5:
Cho tam giác ABC. Hãy vẽ một tam giác đồng dạng với tam giác ABC theo tỉ số .
Xem đáp án
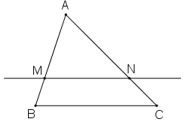
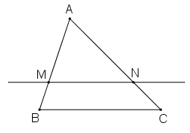
Gọi M là trung điểm AB, N là trung điểm AC.
⇒ MN là đường trung bình của tam giác ABC
⇒ MN // BC
⇒ ΔAMN ΔABC theo tỉ số 
Kiến thức áp dụng
Nếu một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.
ΔABC, MN // BC (M ∈ AB, N ∈ AC) ⇒ ΔAMN ΔABC.
Câu 6:
Cho tam giác ABC, vẽ tam giác A'B'C' đồng dạng với tam giác ABC theo tỉ số đồng dạng k = .
Xem đáp án
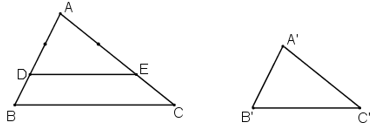
+ Dựng ΔADE ΔABC theo tỉ số 
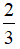
Trên AB lấy D, trên AC lấy E sao cho 
Khi đó theo định lý Ta - let đảo ta suy ra DE // BC
⇒ ΔADE 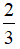ΔABC theo tỉ số (định lý)
+ Dựng ΔA’B’C’ = ΔADE
Vẽ đoạn A’B’ = AD.
Dựng góc 
Trên tia B’x lấy điểm C’ sao cho B’C’ = DE.
Nối C’A’ ta được ΔA’B’C’ = ΔADE (c.g.c)
Suy ra: ΔA’B’C’ đồng dạng với ΔADE theo tỉ số:
Câu 7:
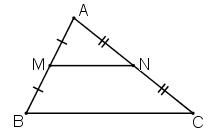
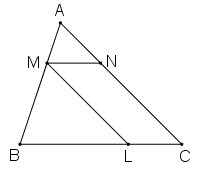
Từ điểm M thuộc cạnh AB của tam giác ABC với AM = MB, kẻ các tia song song với AC và BC, chúng cắt BC và AC lần lượt tại L và N.
a) Nêu tất cả các cặp tam giác đồng dạng.
b) Đối với mỗi cặp tam giác đồng dạng. Hãy viết các cặp góc bằng nhau và tỉ số đồng dạng tương ứng.
Xem đáp án
a) ΔABC có MN // BC (M ∈ AB; N ∈ AC)
⇒ ΔAMN ΔABC (định lí)
ΔABC có ML // AC (M ∈ AB; L ∈ BC)
⇒ ΔMBL ΔABC (định lí)
Vì ΔAMN ΔABC và ΔMBL ΔABC
⇒ ΔAMN ΔMBL.
b) Xét ΔAMN ΔABC có:
Xét ΔMBL ΔABC có:
Xét ΔAMN ΔMBL có:
Kiến thức áp dụng
+ Nếu một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.
ΔABC, MN // BC (M ∈AB, N ∈ AC) ⇒ ΔAMN ΔABC.
+ Nếu ΔABC ΔA’B’C’ và ΔA’B’C’ ΔA”B”C” thì ΔABC ΔA”B”C”.
Câu 8:
ΔA'B'C' ΔABC theo tỉ số đồng dạng k = 
.
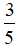a) Tính tỉ số chu vi của hai tam giác đã cho.
b) Cho biết hiệu chu vi của hai tam giác là 40dm, tính chu vi của mỗi tam giác.
Xem đáp án
a) Gọi chu vi tam giác A’B’C’ là P’ và chu vi tam giác ABC là P.
ΔA'B'C' ΔABC theo tỉ số đồng dạng k =
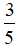
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
Vậy tỉ số chu vi tam giác A’B’C’ và tam giác ABC là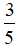
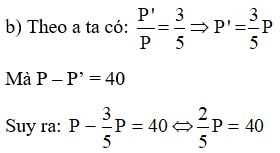
⇒ P = 100 ⇒ P’ = 60.
Vậy chu vi tam giác ABC bằng 100 dm và chu vi tam giác A’B’C’ là 60 dm.
Kiến thức áp dụng
+ ΔABC ΔA’B’C’.
Tỉ số đồng dạng là tỉ số giữa các cạnh tương ứng:
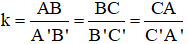
+ Tính chất dãy tỉ số bằng nhau:
Nếu ta có: 
thì 