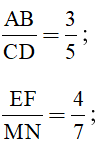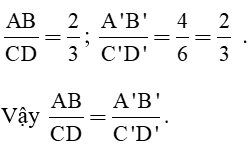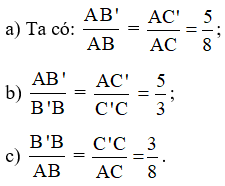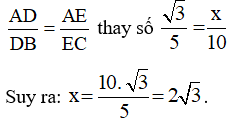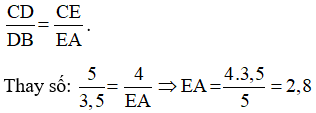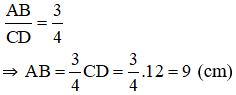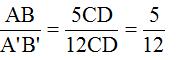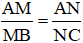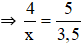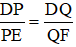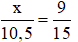Bài 1: Định lí Ta-lét trong tam giác
-
3522 lượt thi
-
9 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 4:
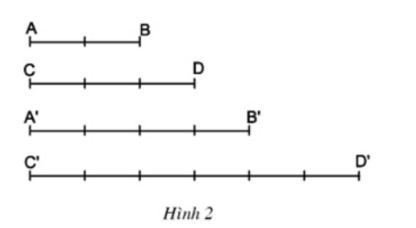
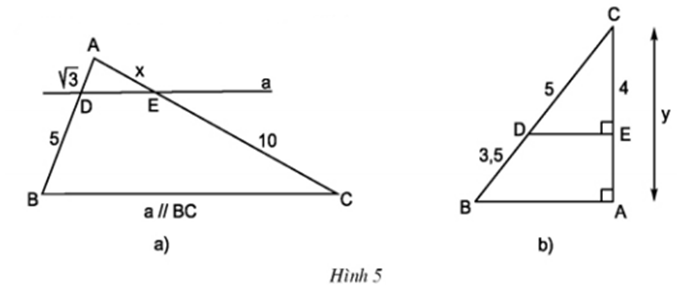
Tính các độ dài x và y trong hình 5.
Xem đáp án
a) Vì a // BC, theo định lí Ta – lét ta có:
b) Vì DE // AB (cùng ⊥ AC), theo định lí Ta – lét ta có:
⇒ y = 4 + 2,8 = 6,8
Câu 5:
Viết tỉ số của hai đoạn thẳng có độ dài như sau:
a) AB = 5cm và CD = 15 cm
b) EF = 48cm và GH = 16dm
c) PQ = 1,2m và MN = 24cm
Xem đáp án
Kiến thức áp dụng
Tỉ số của hai đoạn thẳng là tỉ số độ dài của chúng theo cùng một đơn vị đo.
Câu 6:
Cho biết và CD bằng 12cm. Tính độ dài của AB.
Xem đáp án
Thay CD = 12cm vào tỉ số độ dài ta được:
Vậy độ dài AB = 9cm
Kiến thức áp dụng
Tỉ số của hai đoạn thẳng là tỉ số độ dài của chúng theo cùng một đơn vị đo.
Câu 7:
Cho biết độ dài của AB gấp 5 lần độ dài của CD và độ dài của A'B' gấp 12 lần độ dài của CD. Tính tỉ số của hai đoạn thẳng AB và A'B'.
Xem đáp án
Độ dài AB gấp 5 lần độ dài của CD nên AB = 5CD.
Độ dài A'B' gấp 12 lần độ dài của CD nên A'B' = 12CD.
⇒ Tỉ số của hai đoạn thẳng AB và A'B' là:
Kiến thức áp dụng
Tỉ số của hai đoạn thẳng là tỉ số độ dài của chúng theo cùng một đơn vị đo.
Câu 8:
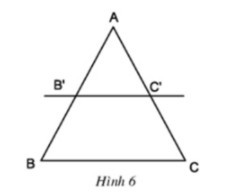
Cho biết (h.6). Chứng minh rằng:
Hướng dẫn: Áp dụng tính chất của tỉ lệ thức.
Xem đáp án
Kiến thức áp dụng
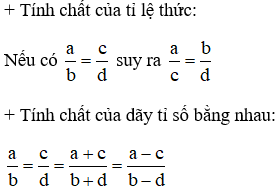
Câu 9:
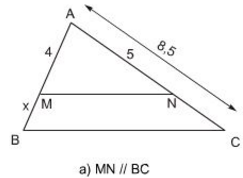
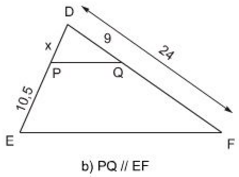
Tính x trong các trường hợp sau (h.7):
Xem đáp án
a) Ta có: MN // BC
Áp dụng định lý Ta-let ta có: 
Mà AM = 4, AN = 5, NC = AC – AN = 8,5 – 5 = 3,5
⇒ 5x = 4.3,5
⇔ 5x = 14
x = 14:5 = 2,8
Vậy x = 2,8
b) Ta có PQ // EF
Áp dụng định lý Talet trong tam giác DEF ta có: 
Mà DP = x, PE = 10,5 ; DQ = 9 ; QF = DF – DQ = 24 – 9 = 15
Do đó ta có : 
⇒ 15x = 9.10,5
⇔ 15x = 94,5
⇔ x = 94,5:15 = 6,3
Vậy x = 6,3.
Kiến thức áp dụng
Định lý Talet: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.
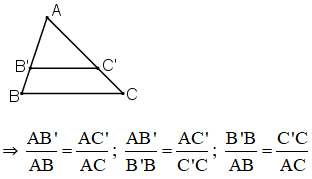
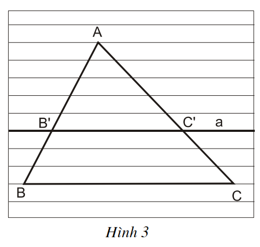
Cho ΔABC, B’C’ // BC
