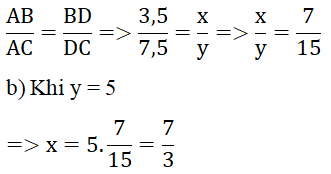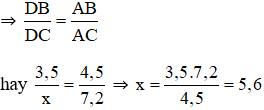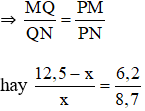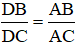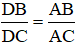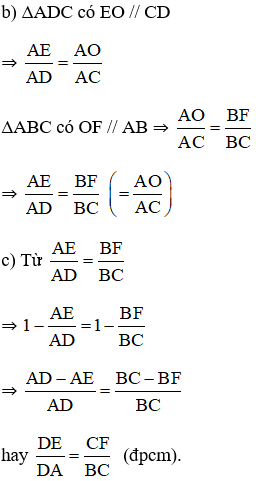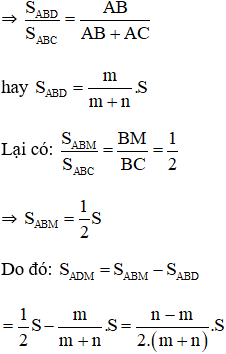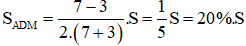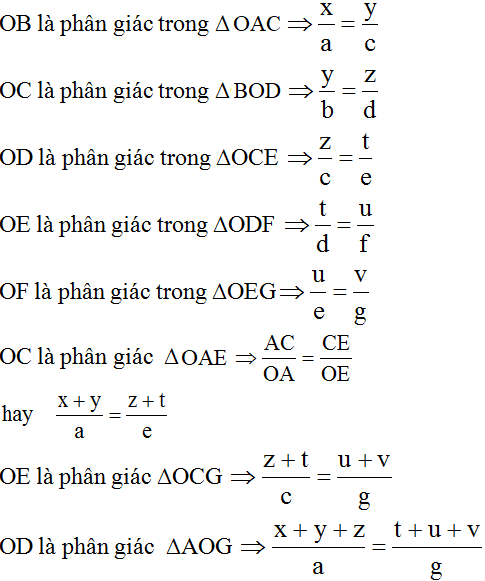Bài 3: Tính chất đường phân giác của tam giác
-
3520 lượt thi
-
11 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
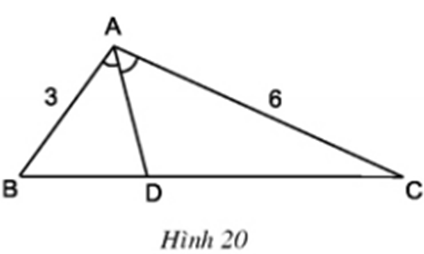
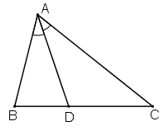
Vẽ tam giác ABC, biết:
AB = 3cm; AC = 6cm; = 100o.
Dựng đường phân giác AD của góc A (bằng compa, thước thẳng), đo độ dài các đoạn thẳng DB, DC rồi so sánh các tỉ số (h.20).
Xem đáp án
Dùng thước đo độ dài ta được: BD ≈ 2 cm; DC ≈ 4 cm.
Suy ra:
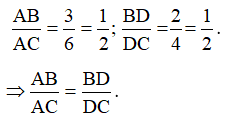
Câu 2:
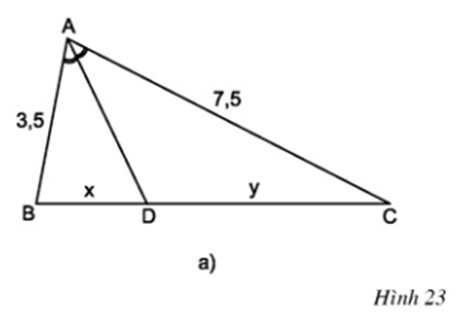
Xem hình 23a.
a) Tính .
b) Tính x khi y = 5.
Xem đáp án
a) Dựa vào tính chất đường phân giác của tam giác, ta có
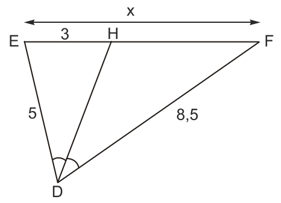
Câu 3:
Tính x trong hình 23b.
Xem đáp án
Dựa vào tính chất đường phân giác của tam giác, ta có:
Vậy x = 8,1.
Câu 4:
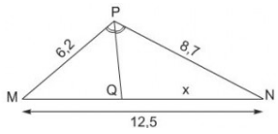
Tính x trong hình 24 và làm tròn kết quả đến chữ số thập phân thứ nhất.
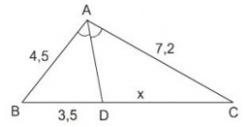
Hình 24
Xem đáp án
Áp dụng tính chất đường phân giác trong các tam giác ta có:
a) ΔABC có AD là đường phân giác
b) Ta có: MQ + QN = MN nên MQ = MN - QN = 12,5 - x
ΔPMN có PQ là phân giác
⇔ 8,7.(12,5 – x) = x.6,2
⇔ 108,75 – 8,7.x = 6,2.x
⇔ 108,75 = 14,9x hay 14,9.x = 108,75
⇔ x ≈ 7,3.
Kiến thức áp dụng
Tính chất đường phân giác của tam giác:
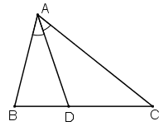
Trong một tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy.
ΔABC, phân giác AD (D ∈ BC) ⇒ 
Câu 5:
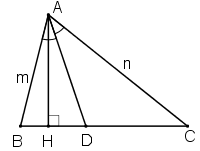
Tam giác ABC có độ dài các cạnh AB = m, AC = n và AD là đường phân giác. Chứng minh rằng tỉ số diện tích của tam giác ABD và diện tích của tam giác ACD bằng .
Xem đáp án
Kẻ AH là đường cao của tam giác ABC
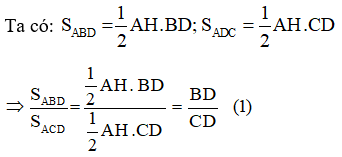
Vì tam giác ABC có AD là đường phân giác nên:
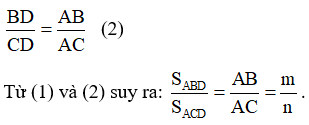
Vậy tỉ số diện tích của tam giác ABD và tam giác ACD bằng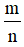 
.
Kiến thức áp dụng
+ Diện tích tam giác bằng một nửa tích của một cạnh và chiều cao tương ứng.
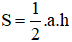
+ Tính chất đường phân giác của tam giác:
Trong một tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy.
ΔABC, phân giác AD (D ∈ BC) ⇒ 
Câu 6:
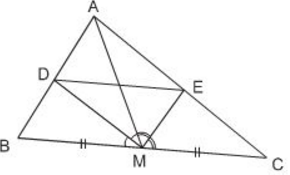
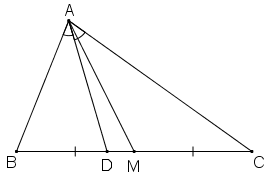
Cho tam giác ABC với đường trung tuyến AM. Tia phân giác của góc AMB cắt cạnh AB ở D, tia phân giác của góc AMC cắt cạnh AC ở E. Chứng minh rằng DE // BC (h.25).
Hình 25
Xem đáp án
Kiến thức áp dụng
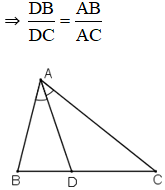
+ Tính chất đường phân giác của tam giác: Trong một tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy.
ΔABC, phân giác AD (D ∈ BC)
+ Định lý Ta-let đảo: Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
ΔABC, B’ ∈ AB, C’ ∈ AC.
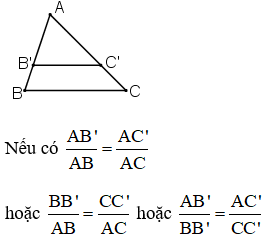
⇒ B’C’ // BC.
Câu 7:
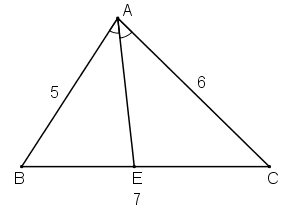
Tam giác ABC có AB = 5cm, AC = 6cm và BC = 7cm. Tia phân giác của góc BAC cắt cạnh BC tại E. Tính các đoạn EB, EC.
Xem đáp án
Kiến thức áp dụng
+ Tính chất đường phân giác của tam giác:
Trong một tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy.
ΔABC, phân giác AD (D ∈ BC) ⇒
+ Tính chất dãy tỉ số bằng nhau:
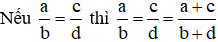
Câu 8:
Cho hình thang ABCD (AB // CD).
Đường thẳng a song song với DC, cắt các cạnh AD và BC theo thứ tự tại E và F. Chứng minh rằng:
;
;
Xem đáp án
Kiến thức áp dụng
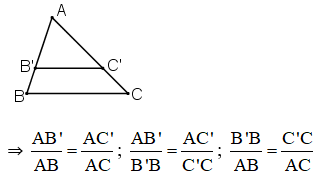
Định lý Talet: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.
Cho ΔABC, B’C’ // BC
Câu 9:
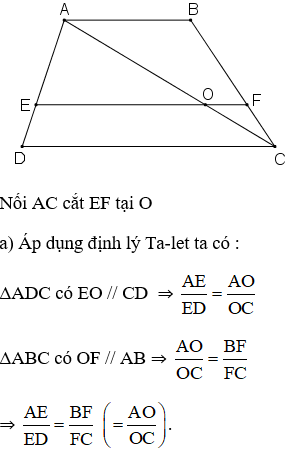
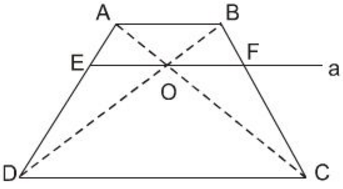
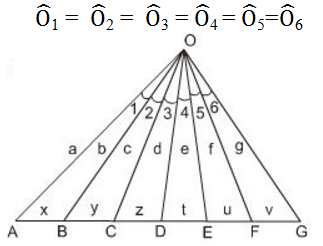
Cho hình thang ABCD (AB // CD). Hai đường chéo AC và BD cắt nhau tại O. Đường thẳng a qua O và song song với đáy của hình thang cắt các cạnh AD, BC theo thứ tự tại E và F (h.26).
Chứng minh rằng OE = OF
Xem đáp án
Kiến thức áp dụng
+ Định lý Talet: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.
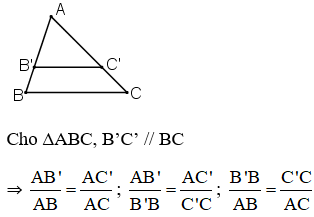
+ Hệ quả định lý Ta-let : Nếu một đường thẳng cắt hai cạnh (hoặc cạnh kéo dài) của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
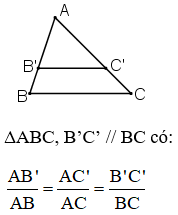
Câu 10:
a) Cho tam giác ABC với đường trung tuyến AM và đường phân giác trong AD. Tính diện tích tam giác ADM, biết AB = m, AC = n (n > m) và diện tích tam giác ABC là S.
b) Khi cho n = 7cm, m = 3cm, hỏi rằng diện tích tam giác ADM chiếm bao nhiêu phần trăm diện tích tam giác ABC?
Xem đáp án
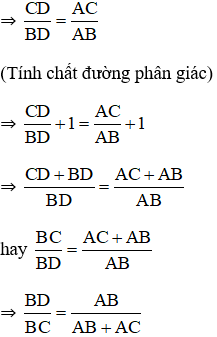
a) Ta có: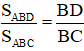 
(do hai tam giác có chung chiều cao từ đỉnh A)
ΔABC có AD là phân giác
b) Với n = 7; m = 3, thay vào kết quả phần a ta có:
Vậy diện tích tam giác ADM chiếm 20% diện tích tam giác ABC.
Kiến thức áp dụng
+ Tính chất đường phân giác của tam giác:
Trong một tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy.
ΔABC, phân giác AD (D ∈ BC) ⇒
