5 câu hỏi trắc nghiệm thuộc Đề số 3. Top 10 Đề kiểm tra Giữa kì 1 Toán 8 (có đáp án)

Top 10 Đề kiểm tra Giữa kì 1 Toán 8 (có đáp án)

Đề số 3. Top 10 Đề kiểm tra Giữa kì 1 Toán 8 (có đáp án)

4113 lượt thi
5 câu hỏi
30 phút

Danh sách câu hỏi

Câu 1:

2 x (3 x^{2} - 4 x + 2)

2 x (3 x + 5) - 3 (2 x^{2} - 2 x + 3)

(2 x + 1) (3 x^{2} - x + 2)

2) Tính giá trị của biểu thức

A = x^{2} - 6 x y + 9 y^{2} - 15

tại

x = 37

;

y = - 1

Xem đáp án

1) Thực hiện phép tính:
a)

2 x (3 x^{2} - 4 x + 2) = 2 x .3 x^{2} - 2 x .4 x + 2 x .2 = 6 x^{3} - 8 x^{2} + 4 x .

2 x (3 x + 5) - 3 (2 x^{2} - 2 x + 3) = 2 x .3 x + 2 x .5 - 3.2 x^{2} + 3.2 x - 3.3 = 6 x^{2} + 10 x - 6 x^{2} + 6 x - 9 = 16 x - 9

(2 x + 1) (3 x^{2} - x + 2) = 2 x .3 x^{2} - 2 x . x + 2 x .2 + 1.3 x^{2} - 1. x + 1.2 = 6 x^{3} - 2 x^{2} + 4 x + 3 x^{2} - x + 2 = 6 x^{3} + x^{2} + 3 x + 2

2. Tính giá trị của biểu thức tại

A = x^{2} - 6 x y + 9 y^{2} - 15

; tại

x = 37

;

y = - 1

Ta có

A = x^{2} - 6 x y + 9 y^{2} - 15 = x^{2} - 2. x .3 y + {(3 y)}^{2} - 15 = {(x - 3 y)}^{2} - 15

Thay

x = 37

;

y = - 1

vào biểu thức ta có

A = {(x - 3 y)}^{2} - 15

Ta có

A = {(37 - 3. (- 1))}^{2} - 15 = {(37 + 3)}^{2} - 15 = 40^{2} - 15 = 1600 - 15 = 1585

Vậy giá trị của biểu thức

A = x^{2} - 6 x y + 9 y^{2} - 15

tại

x = 37

;

y = - 1

là 1585

Câu 2:

Phân tích các đa thức sau thành nhân tử
a)

9 x^{2} y + 15 x y^{2} - 3 x

3 z (z - 2) + 5 (2 - z)

x^{2} + 4 x y - 4 z^{2} + 4 y^{2}

x^{2} + 2 x - 15

Xem đáp án

a, $9 x^{2} y + 15 x y^{2} - 3 x = 3 x (3 x y + 5 y^{2} - 1)$

b, $3 z (z - 2) + 5 (2 - z) = 3 z (z - 2) - 5 (z - 2) = (3 z - 5) (z - 2)$

c, $x^{2} + 4 x y - 4 z^{2} + 4 y^{2} = (x^{2} + 4 x y + 4 y^{2}) - 4 z^{2}$ $= {(x + 2 y)}^{2} - {(2 z)}^{2} = (x + 2 y - 2 z) (x + 2 y + 2 z)$

d, $x^{2} + 2 x - 15 = x^{2} - 3 x + 5 x - 15 = x (x - 3) + 5 (x - 3)$ $= (x - 3) (x + 5)$

Câu 3:

Tìm biết:
a)

x^{2} - 4 x = 0

{(2 x + 1)}^{2} - 4 x (x + 3) = 9

x^{2} - 12 x = - 36

Xem đáp án

x^{2} - 4 x = 0

\Leftrightarrow x (x - 4) = 0 \Leftrightarrow [\begin{array}{l} x = 0 \\ x - 4 = 0 \end{array} \Leftrightarrow [\begin{array}{l} x = 0 \\ x = 4 \end{array}

Vậy,

x \in \{0; 4\}

{(2 x + 1)}^{2} - 4 x (x + 3) = 9

\Leftrightarrow 4 x^{2} + 4 x + 1 - 4 x^{2} - 12 x - 9 = 0

\Leftrightarrow - 8 x - 8 = 0 \Leftrightarrow - 8 (x + 1) = 0

\Leftrightarrow x + 1 = 0

\Leftrightarrow x = - 1

Vậy

x = - 1

x^{2} - 12 x = - 36 \Leftrightarrow x^{2} - 12 x + 36 = 0 \Leftrightarrow {(x - 6)}^{2} = 0 \Leftrightarrow x - 6 = 0 \Leftrightarrow x = 6

Vậy

x = 6

Câu 4:

Cho hình bình hành ABCD, trên tia đối của tia AD lấy điểm E sao cho $A E = A D .$ Gọi là giao điểm của EC và AB

a) Chứng minh tứ giác AEBC là hình bình hành.

b) Chứng minh $F E = F C .$

c) Trên tia đối của tia CD lấy điểm M sao cho $M C = C D .$ Chứng minh ba điểm E, B, M thẳng hàng.

Xem đáp án

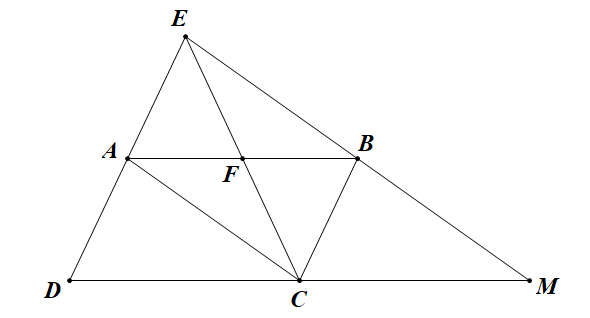
Cho hình bình hành ABCD, trên tia đối của tia AD lấy điểm E sao cho Gọi là giao điểm của EC và (ảnh 1)

a) Chứng minh tứ giác AEBC là hình bình hành.
Vì tứ giác ABCD là hình bình hành suy ra

A D // B C

và

A D = B C .

A B // C D

và

A B = D C .

Xét tứ giác AEBC có:

A E // B C

(do

A D // B C

và E, A, D thẳng hàng) và

A E = B C (= A D) .

Suy ra tứ giác là hình bình hành (dấu hiệu nhận biết).
b) Chứng minh

F E = F C .

Hình bình hành AEBC có hai đường chéo là AB và EC. Mà F là giao điểm của EC và AB nên suy ra F là trung điểm mỗi đoạn (tính chất).
F là trung điểm EC nên

F C = F E .

c) Trên tia đối của tia CD lấy điểm M sao cho

M C = C D .

Chứng minh ba điểm E, B, M thẳng hàng.
Xét tứ giác ABMC có:

A B // C M

(do

A B // D C

và D, C, M thẳng hàng) và

A B = C M (= D C) .

Suy ra tứ giác ABMC là hình bình hành (dấu hiệu nhận biết). Suy ra

A C // B M

(tính chất).
Vì tứ giác AEBC là hình bình hành nên

A C // E B

(tính chất).
Từ đó suy ra EB trùng BM. Vậy ba điểm E, B, M thẳng hàng (đpcm).

Câu 5:

Tìm giá trị nhỏ nhất của biểu thức sau: $A = x^{2} + y^{2} + z^{2} - y z - 4 x - 3 y + 2027$

Xem đáp án

A = x^{2} + y^{2} + z^{2} - y z - 4 x - 3 y + 2027 = x^{2} - 4 x + 4 + \frac{1}{4} y^{2} - y z + z^{2} + \frac{3}{4} y^{2} - 3 y + 3 + 2020 = (x^{2} - 4 x + 4) + (\frac{1}{4} y^{2} - y z + z^{2}) + 3 (\frac{1}{4} y^{2} - y + 1) + 2020 = {(x - 2)}^{2} + {(\frac{1}{2} y - z)}^{2} + 3 {(\frac{1}{2} y - 1)}^{2} + 2020

Vì

{(x - 2)}^{2} \geq 0

;

{(\frac{1}{2} y - z)}^{2} \geq 0

;

3 {(\frac{1}{2} y - 1)}^{2} \geq 0

với mọi

x, y, z

nên

A = {(x - 2)}^{2} + {(\frac{1}{2} y - z)}^{2} + 3 {(\frac{1}{2} y - 1)}^{2} + 2020 \geq 2020

với mọi
Dấu “=” xảy ra khi và chỉ khi

{(x - 2)}^{2} = 0

;

{(\frac{1}{2} y - z)}^{2} = 0

;

3 {(\frac{1}{2} y - 1)}^{2} = 0

Suy ra

x - 2 = 0

;

\frac{1}{2} y - z = 0

;

3 (\frac{1}{2} y - 1) = 0

Suy ra

x = 2

;

\frac{1}{2} y = z

;

\frac{1}{2} y = 1

Suy ra

x = 2

;

y = 2

;

z = 1

Vậy giá trị nhỏ nhất của là khi

x = 2; y = 2; z = 1

Bắt đầu thi ngay

CHỌN BỘ SÁCH BẠN MUỐN XEM

Top 10 Đề kiểm tra Giữa kì 1 Toán 8 (có đáp án)

Đề số 3. Top 10 Đề kiểm tra Giữa kì 1 Toán 8 (có đáp án)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương