Đề số 7. Top 10 Đề kiểm tra Giữa kì 1 Toán 8 (có đáp án)
-
4905 lượt thi
-
6 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Cho hai biểu thức và
a) Tính giá trị của biểu thức A khi
b) Chứng tỏ rằng với mọi giá trị của biến x.
c) Tìm giá trị nhỏ nhất của biểu thức
a) Tính giá trị của biểu thức A khi
b) Chứng tỏ rằng với mọi giá trị của biến x.
c) Tìm giá trị nhỏ nhất của biểu thức
 Xem đáp án
Xem đáp án
a) Thay vào biểu thức A
Tính được
b)
c) Ta có
Giá trị nhỏ nhất của biểu thức C là tại x =
Tính được
b)
c) Ta có
Giá trị nhỏ nhất của biểu thức C là tại x =
Câu 4:
Cho hình vẽ bên, biết , , . Tính EG.
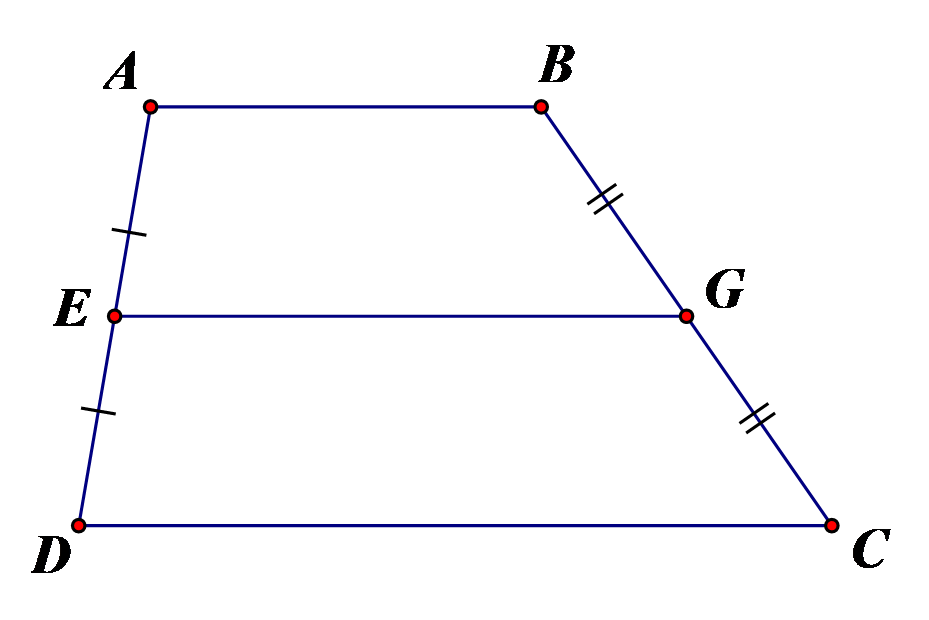
 Xem đáp án
Xem đáp án
Ta có (gt) nên tứ giác ABCD là hình thang.
Mà E, G lần lượt là trung điểm của AD, BC (gt)
Suy ra EG là đường trung bình của hình thang ABCD.
.
Mà E, G lần lượt là trung điểm của AD, BC (gt)
Suy ra EG là đường trung bình của hình thang ABCD.
.
Câu 5:
Cho có E là trung điểm của AC. Qua E kẻ ;
a) Chứng minh rằng tứ giác BDEF là hình bình hành và D là trung điểm của đoạn thẳng BC.
a) Chứng minh rằng tứ giác BDEF là hình bình hành và D là trung điểm của đoạn thẳng BC.
b) Gọi H là điểm đối xứng của D qua H. Chứng minh rằng HB//AD.
c) Gọi I là trung điểm của HB; K là giao điểm của AD và EF. Chứng minh rằng I; K; E thẳng hàng.
d) cần có thêm điều kiện gì để .
c) Gọi I là trung điểm của HB; K là giao điểm của AD và EF. Chứng minh rằng I; K; E thẳng hàng.
d) cần có thêm điều kiện gì để .
 Xem đáp án
Xem đáp án
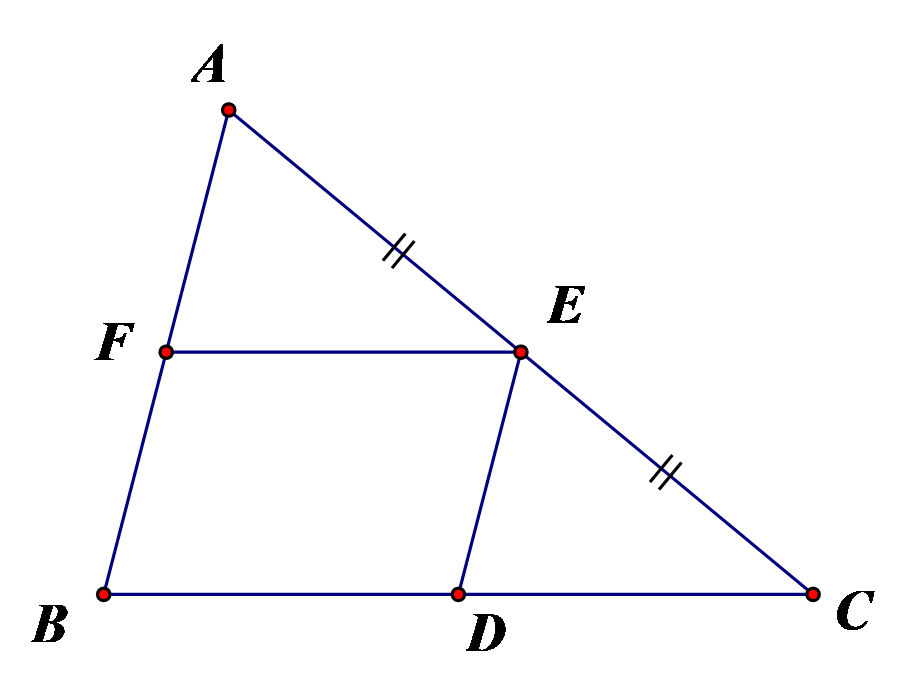
a) + Xét tứ giác BDEF có: (vì - gt)
(vì - gt)
là hình bình hành (DHNB).
+ Xét có: E là trung điểm của AC và
Suy ra D là trung điểm của đoạn thẳng BC (định lý đường trung bình trong tam giác).
(vì - gt)
là hình bình hành (DHNB).
+ Xét có: E là trung điểm của AC và
Suy ra D là trung điểm của đoạn thẳng BC (định lý đường trung bình trong tam giác).

Vì
Và
Ta có: , mà F là trung điểm của AB và HD
tứ giác AHBD là hình bình hành (đpcm).
Và
Ta có: , mà F là trung điểm của AB và HD
tứ giác AHBD là hình bình hành (đpcm).

c)
Ta có: FD là đường trung bình của
tứ giác FDEA là hình bình hành.
(gt), K là trung điểm của AD.
Và I là trung điểm của HB.
là đường trung bình của hình bình hành AHBD.
(1)
Tương tự: I là trung điểm của HB
E là trung điểm của AC
là đường trung bình của hình thang AHBC
(2)
Từ (1) và (2) có I, K, E thẳng hàng. (dpcm)
Ta có: FD là đường trung bình của
tứ giác FDEA là hình bình hành.
(gt), K là trung điểm của AD.
Và I là trung điểm của HB.
là đường trung bình của hình bình hành AHBD.
(1)
Tương tự: I là trung điểm của HB
E là trung điểm của AC
là đường trung bình của hình thang AHBC
(2)
Từ (1) và (2) có I, K, E thẳng hàng. (dpcm)
d) Xét hình bình hành AHBD có:
Và
Để
Hình bình hành AHBD có hai đường chéo HD và AB bằng nhau
là hình chữ nhật là đường cao của tam giác ABC
Mặt khác, D là trung điểm của BC (theo cm câu a)
Suy ra AD là đường trung tuyến của tam giác ABC
Tam giác ABC có AD vừa là đường cao, vừa là trung tuyến cân tại A.
Vậy, để thì phải cân tại A
Và
Để
Hình bình hành AHBD có hai đường chéo HD và AB bằng nhau
là hình chữ nhật là đường cao của tam giác ABC
Mặt khác, D là trung điểm của BC (theo cm câu a)
Suy ra AD là đường trung tuyến của tam giác ABC
Tam giác ABC có AD vừa là đường cao, vừa là trung tuyến cân tại A.
Vậy, để thì phải cân tại A
