5 câu hỏi trắc nghiệm thuộc Đề số 5. Top 10 Đề kiểm tra Giữa kì 1 Toán 8 (có đáp án)

Top 10 Đề kiểm tra Giữa kì 1 Toán 8 (có đáp án)

Đề số 5. Top 10 Đề kiểm tra Giữa kì 1 Toán 8 (có đáp án)

4106 lượt thi
5 câu hỏi
30 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

a) Thực hiện phép tính:

$(3 x - 1) (2 x + 7) - (12 x^{3} + 8 x^{2} - 14 x) : 2 x$

b) Không dùng máy tính bỏ túi, tính nhanh giá trị biểu thức:

$B = (63^{3} - 37^{3}) : 26 + 63.37$

Xem đáp án

a) Thực hiện phép tính:

(3 x - 1) (2 x + 7) - (12 x^{3} + 8 x^{2} - 14 x) : 2 x

\begin{array}{l} (3 x - 1) (2 x + 7) - (12 x^{3} + 8 x^{2} - 14 x) : 2 x \\ = 6 x^{2} + 19 x - 7 - (6 x^{2} + 4 x - 7) \\ = 6 x^{2} + 19 x - 7 - 6 x^{2} - 4 x + 7 \\ = 15 x \end{array}

b) Không dùng máy tính bỏ túi, tính nhanh giá trị biểu thức:

B = (63^{3} - 37^{3}) : 26 + 63.37 \begin{array}{l} B = (63^{3} - 37^{3}) : 26 + 63.37 \\ = (63 - 37) (63^{2} + 63.37 + 37^{2}) : 26 + 63.37 \\ = 26 (63^{2} + 63.37 + 37^{2}) : 26 + 63.37 \\ = 63^{2} + 63.37 + 37^{2} + 63.37 \\ = 63^{2} + 2.63.37 + 37^{2} \\ = {(63 + 37)}^{2} = 100^{2} \\ = 10000 \end{array}

Câu 2:

Phân tích các đa thức sau thành nhân tử :
a)

x y^{2} - 25 x

x (x - y) + 2 x - 2 y

x^{3} - 3 x^{2} - 4 x + 12

Xem đáp án

x y^{2} - 25 x = x (y^{2} - 25) = x (y - 5) (y + 5)

.
b)

x (x - y) + 2 x - 2 y = x (x - y) + 2 (x - y) = (x - y) (x + 2)

.
c)

x^{3} - 3 x^{2} - 4 x + 12 = x^{2} (x - 3) - 4 (x - 3) = (x - 3) (x^{2} - 4) = (x - 3) (x - 2) (x + 2)

Câu 3:

Tìm x, biết:
a)

{(x + 2)}^{2} + {(x - 1)}^{2} + (x - 3) (x + 3) - 3 x^{2} = - 8

.
b)

2021 x (x - 2020) - x + 2020 = 0

Xem đáp án

a, ${(x + 2)}^{2} + {(x - 1)}^{2} + (x - 3) (x + 3) - 3 x^{2} = - 8$

$\Leftrightarrow x^{2} + 4 x + 4 + x^{2} - 2 x + 1 + x^{2} - 9 - 3 x^{2} = - 8 \Leftrightarrow (x^{2} + x^{2} + x^{2} - 3 x^{2}) + (4 x - 2 x) + (4 + 1 - 9) = - 8 \Leftrightarrow 2 x - 4 = - 8 \Leftrightarrow 2 x = - 4 \Leftrightarrow x = - 2$

Vậy $x = - 2$

$2021 x (x - 2020) - x + 2020 = 0 \Leftrightarrow 2021 x (x - 2020) - (x - 2020) = 0 \Leftrightarrow (x - 2020) (2021 x - 1) = 0 \Leftrightarrow [\begin{array}{l} x - 2020 = 0 \\ 2021 x - 1 = 0 \end{array} \Leftrightarrow [\begin{array}{l} x = 2020 \\ x = \frac{1}{2021} \end{array}$

Vậy $x \in \{\frac{1}{2021}; 2020\}$

Câu 4:

Cho hình bình hành ABCD (AB > AD). Qua A kẻ đường thẳng vuông góc với BD tại E, cắt CD tại I. Qua C kẻ đường thẳng vuông góc với AB tại I, cắt AB tại K.
a) Tứ giác AKCI là hình gì? Vì sao?
b) Chứng minh

A F // C E

.
c) Chứng minh rằng ba đường thẳng AC, EF và KI đồng quy tại một điểm.

Xem đáp án

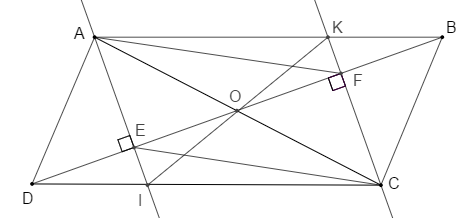
Cho hình bình hành ABCD (AB > AD). Qua A kẻ đường thẳng vuông góc với BD tại E (ảnh 1)

a) Tứ giác là hình gì? Vì sao?
Vì ABCD là hình bình hành

\Rightarrow A B / / D C \Rightarrow A K / / I C

Lại có:

\begin{array}{l} A I ⊥ B D \\ C K ⊥ B D \end{array}\} \Rightarrow A I / / C K

\Rightarrow A I C K

là hình bình hành (tứ giác có hai cặp cạnh đối song song)

b) Chứng minh

A F / / C E

.
Vì ABCD là hình bình hành

\Rightarrow A B = C D

Xét

Δ A B E

và

Δ C D F

có:

\hat{A E B} = \hat{C F D} (= 90^{o})

\hat{A B E} = \hat{C D F}

(cặp góc so le trong)

A B = C D

\Rightarrow Δ A B E = Δ C D F

(ch-gn)

\Rightarrow A E = C F

(hai cạnh tương ứng)
Mà

A E / / C F \Rightarrow A E C F

là hình bình hành (tứ giác có cặp cạnh đối song song và bằng nhau)

\Rightarrow A F / / C E

c) Chứng minh rằng ba đường thẳng AC, EF và KI đồng quy tại một điểm.
Ta có tứ giác AKCI là hình bình hành (chứng minh trên)
Nên giả sử giao điểm hai đường chéo AC và KI của hình bình hành AKCI là O