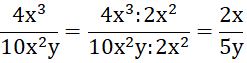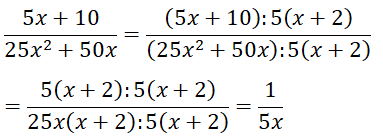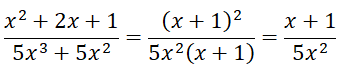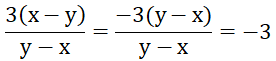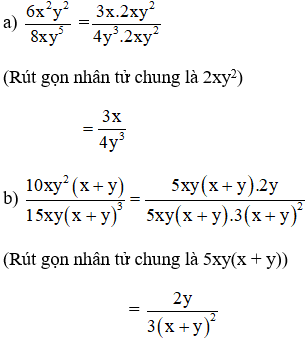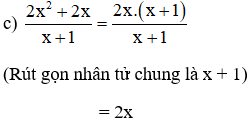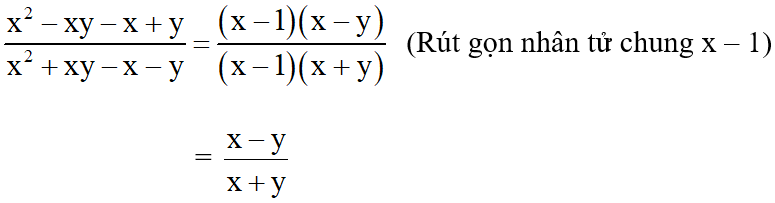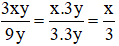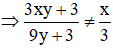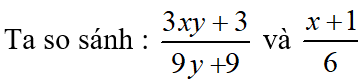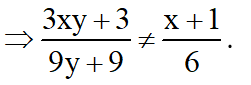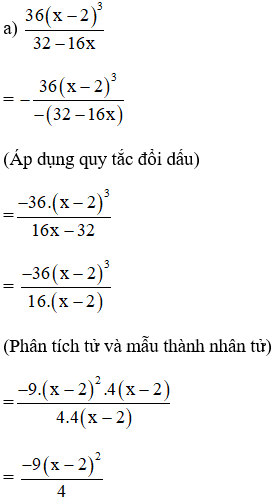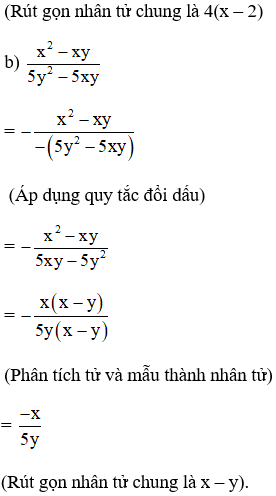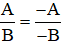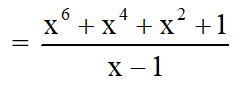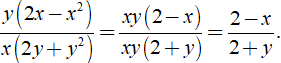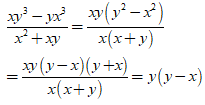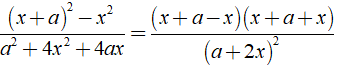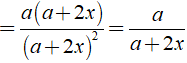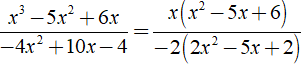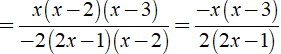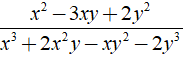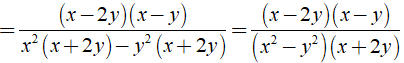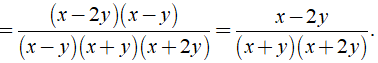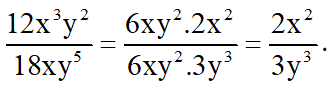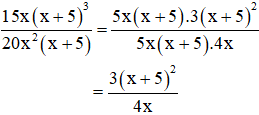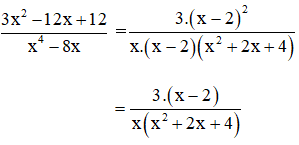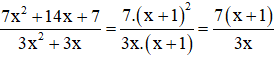13 câu hỏi trắc nghiệm thuộc Bài 3: Rút gọn phân thức

Câu 1:

Cho phân thức: $\frac{4 x^{3}}{10 x^{2} y}$ $\frac{4 x^{3}}{10 x^{2} y}$

a) Tìm nhân tử chung của cả tử và mẫu.

b) Chia cả tử và mẫu cho nhân tử chung.

Xem đáp án

a) Nhân tử chung của cả tử và mẫu: 2x²

b)

Câu 2:

Cho phân thức: $\frac{5 x + 10}{25 x^{2} + 50 x}$ $\frac{5 x + 10}{25 x^{2} + 50 x}$

a) Phân tích tử và mẫu thành nhân tử rồi tìm nhân tử chung của chúng.

b) Chia cả tử và mẫu cho nhân tử chung.

Xem đáp án

a) 5x + 10 = 5(x + 2)

25x² + 50x = 25x(x + 2)

⇒ Nhân tử chung của chúng là: 5(x + 2)

b)

Câu 3:

Rút gọn phân thức: $\frac{x^{2} + 2 x + 1}{5 x^{3} + 5 x^{2}}$ $\frac{x^{2} + 2 x + 1}{5 x^{3} + 5 x^{2}}$

Xem đáp án

Câu 4:

Rút gọn phân thức: $\frac{3 (x - y)}{y - x}$ $\frac{3 (x - y)}{y - x}$

Xem đáp án

Câu 5:

Rút gọn phân thức:

$a) \frac{6 x^{2} y^{2}}{8 x y^{5}};$ $a) \frac{6 x^{2} y^{2}}{8 x y^{5}};$

$b) \frac{10 x y^{2} (x + y)}{15 x y {(x + y)}^{3}};$ $b) \frac{10 x y^{2} (x + y)}{15 x y {(x + y)}^{3}};$

$c) \frac{2 x^{2} + 2 x}{x + 1};$ $c) \frac{2 x^{2} + 2 x}{x + 1};$

$d) \frac{x^{2} - x y - x + y}{x^{2} + x y - x - y} .$ $d) \frac{x^{2} - x y - x + y}{x^{2} + x y - x - y} .$

Xem đáp án

d)

+ Phân tích tử số thành nhân tử :

x² – xy – x + y = (x² – xy) – (x – y) = x.(x – y) – (x – y) = (x – 1)(x – y)

+ Phân tích mẫu số thành nhân tử :

x² + xy – x – y = (x² + xy) – (x + y) = x(x + y) – (x + y) = (x – 1)(x + y)

Do đó ta có :

Kiến thức áp dụng

Muốn rút gọn một phân thức ta có thể :

+ Phân tích cả tử và mẫu thành nhân tử để tìm nhân tử chung.

+ Rút gọn cả tử và mẫu cho nhân tử chung.

Câu 6:

Trong tờ nháp của một bạn có ghi một số phép rút gọn phân thức như hình sau:

$a) \frac{3 x y}{9 y} = \frac{x}{3};$ $a) \frac{3 x y}{9 y} = \frac{x}{3};$

$b) \frac{3 x y + 3}{9 y + 3} = \frac{x}{3};$ $b) \frac{3 x y + 3}{9 y + 3} = \frac{x}{3};$

$c) \frac{3 x y + 3}{9 y + 9} = \frac{x + 1}{3 + 3} = \frac{x + 1}{6};$ $c) \frac{3 x y + 3}{9 y + 9} = \frac{x + 1}{3 + 3} = \frac{x + 1}{6};$

$d) \frac{3 x y + 3 x}{9 y + 9} = \frac{x}{3} .$ $d) \frac{3 x y + 3 x}{9 y + 9} = \frac{x}{3} .$

Theo em câu nào đúng, câu nào sai? Em hãy giải thích.

Xem đáp án

a) Đúng vì rút gọn cả tử và mẫu cho 3y

b) Sai vì

(3xy + 3).3 = 3xy.3 + 3.3 = 9xy + 9

(9y + 3).x = 9y.x + 3.x = 9xy + 3x

Do đó (3xy + 3).3 ≠ (9y + 3).x

c) Sai.

Ta có: (3xy + 3).6 = 3xy.6 + 3.6 = 18xy + 18

Và (9x + 9).(x + 1) = 9xy + 9y + 9x + 9

Do đó (3xy + 3).6 ≠ (9x + 9).(x + 1)

d) Đúng vì:

(Rút gọn cả tử và mẫu cho nhân tử chung 3y + 3).

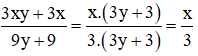
Kiến thức áp dụng

Muốn rút gọn một phân thức ta có thể :

+ Phân tích cả tử và mẫu thành nhân tử để tìm nhân tử chung.

+ Rút gọn cả tử và mẫu cho nhân tử chung.

Câu 7:

Áp dụng qui tắc đổi dấu rồi rút gọn phân thức:

$a) \frac{36 {(x - 2)}^{3}}{32 - 16 x};$ $a) \frac{36 {(x - 2)}^{3}}{32 - 16 x};$

$b) \frac{x^{2} - x y}{5 y^{2} - 5 x y} .$ $b) \frac{x^{2} - x y}{5 y^{2} - 5 x y} .$

Xem đáp án

Kiến thức áp dụng

Quy tắc đổi dấu:

Muốn rút gọn một phân thức ta có thể :

+ Phân tích cả tử và mẫu thành nhân tử để tìm nhân tử chung.

+ Rút gọn cả tử và mẫu cho nhân tử chung.

Câu 8:

Đố. Đố em rút gọn được phân thức: $\frac{x^{7} + x^{6} + x^{5} + x^{4} + x^{3} + x + 1}{x^{2} - 1}$ $\frac{x^{7} + x^{6} + x^{5} + x^{4} + x^{3} + x + 1}{x^{2} - 1}$

Xem đáp án

Phân tích tử số thành nhân tử:

x⁷ + x⁶ + x⁵ + x⁴ + x³ + x² + x + 1

= (x⁷ + x⁶) + (x⁵ + x⁴) + (x³ + x²) + (x + 1)

= x⁶(x + 1) + x⁴(x + 1) + x²(x + 1) + (x + 1)

= (x⁶ + x⁴ + x² + 1)(x + 1)

Phân tích mẫu số thành nhân tử:

x² – 1 = (x – 1)(x + 1)

Do đó:

Kiến thức áp dụng

Muốn rút gọn một phân thức ta có thể :

+ Phân tích cả tử và mẫu thành nhân tử để tìm nhân tử chung.

+ Rút gọn cả tử và mẫu cho nhân tử chung.

Câu 9:

Rút gọn các biểu thức sau

$a) \frac{y (2 x - x^{2})}{x (2 y + y^{2})}$ $a) \frac{y (2 x - x^{2})}{x (2 y + y^{2})}$ ;

$b) \frac{x y^{3} - y x^{3}}{x^{2} + x y}$ $b) \frac{x y^{3} - y x^{3}}{x^{2} + x y}$ ;

$c) \frac{{(x + a)}^{2} - x^{2}}{a^{2} + 4 x^{2} + 4 a x} .$ $c) \frac{{(x + a)}^{2} - x^{2}}{a^{2} + 4 x^{2} + 4 a x} .$

Xem đáp án

a) Ta có:

b) Ta có:

c) Ta có:

Câu 10:

Rút gọn phân thức sau:

$a) \frac{x^{3} - 5 x^{2} + 6 x}{- 4 x^{2} + 10 x - 4};$ $a) \frac{x^{3} - 5 x^{2} + 6 x}{- 4 x^{2} + 10 x - 4};$

$b) \frac{x^{2} - 3 x y + 2 y^{2}}{x^{3} + 2 x^{2} y - x y^{2} - 2 y^{3}} .$ $b) \frac{x^{2} - 3 x y + 2 y^{2}}{x^{3} + 2 x^{2} y - x y^{2} - 2 y^{3}} .$