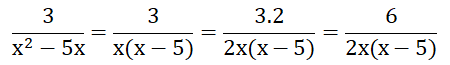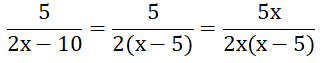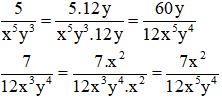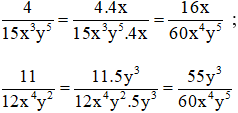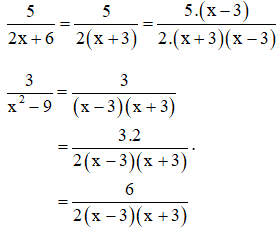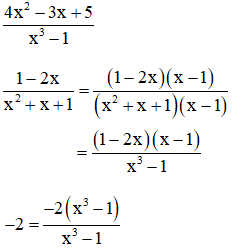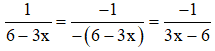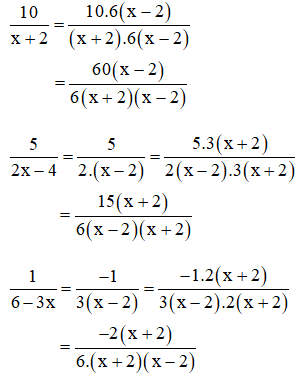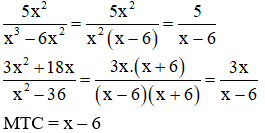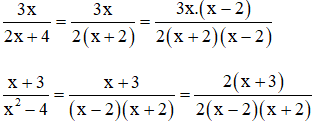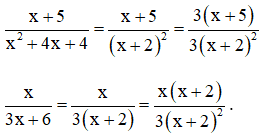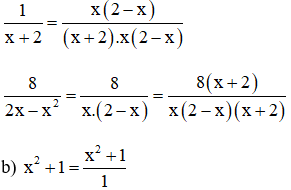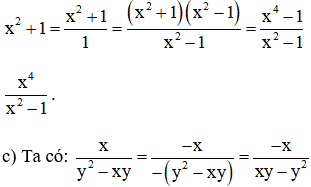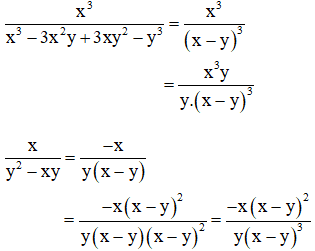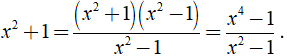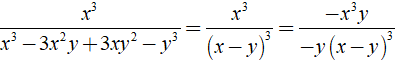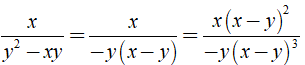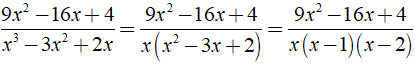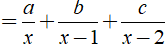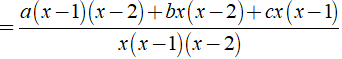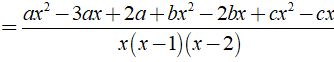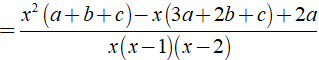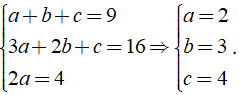11 câu hỏi trắc nghiệm thuộc Bài 4: Quy đồng mẫu thức nhiều phân thức

Câu 1:

Cho hai phân thức $\frac{2}{6 x^{2} y z} v à \frac{5}{4 x y^{3}}$ . Có thể chọn mẫu thức chung là 12x² y³z hoặc 24x³ y⁴z hay không ? Nếu được thì mẫu thức chung nào đơn giản hơn?

Xem đáp án

Có thể chọn mẫu thức chung là 12x²y³ z hoặc 24x³y⁴z

Chọn mẫu thức chung là 12x²y³z đơn giản hơn.

Câu 2:

Quy đồng mẫu thức hai phân thức: $\frac{3}{x^{2} - 5 x}$ và $\frac{5}{2 x - 10}$

Xem đáp án

x² - 5x = x(x - 5)

2x - 10 = 2(x - 5)

=> Mẫu thức chung là: 2x(x-5)

Vì 2x(x - 5) = 2. x(x - 5) = 2 . (x² - 5x) nên phải nhân cả tử và mẫu của phân thức thứ nhất với 2:

Vì 2x(x-5) = x. 2(x-5) = x. (2x – 10) nên phải nhân cả tử và mẫu của phân thức thứ hai với x:

Câu 3:

Qui đồng mẫu thức các phân thức sau:

$a) \frac{5}{x^{5} y^{3}} v à \frac{7}{12 x^{3} y^{4}};$

$b) \frac{4}{15 x^{3} y^{5}} v à \frac{11}{12 x^{4} y^{2}} .$

Xem đáp án

a) Chọn mẫu thức chung đơn giản nhất là 12x⁵y⁴

Nhân tử phụ:

12x⁵y⁴ : x⁵y³ = 12y

12x⁵y⁴ : 12x³y⁴ = x²

Qui đồng:

b) Chọn mẫu thức chung đơn giản nhất là 60x⁴y⁵

Nhân tử phụ:

60x⁴y⁵ : 15x³y⁵ = 4x

60x⁴y⁵ : 12x⁴y² = 5y³

Qui đồng:

Kiến thức áp dụng

- Để tìm mẫu thức chung của nhiều phân thức ta cần:

+ Phân tích các mẫu thức đã cho thành nhân tử

+ Chọn mẫu thức chung là tích của các nhân tử số và các biểu thức xuất hiện ở các mẫu riêng , trong đó :

+ Nhân tử bằng số là BCNN của các nhân tử bằng số ở các mẫu riêng.

+ Với các biểu thức, lấy biểu thức có số mũ cao nhất.

Câu 4:

Qui đồng mẫu thức các phân thức sau:

$a) \frac{5}{2 x + 6} v à \frac{3}{x^{2} - 9} .$

$b) \frac{2 x}{x^{2} - 8 x + 16} v à \frac{x}{3 x^{2} - 12 x} .$

Xem đáp án

a) + Phân tích các mẫu thức thành nhân tử để tìm mẫu thức chung

2x + 6 = 2.(x + 3)

x² – 9 = (x – 3)(x + 3)

⇒ Mẫu thức chung là 2(x + 3)(x – 3)

Nhân tử phụ thứ nhất: x- 3

Nhân tử phụ thứ hai: 2

+ Quy đồng :

b) * Phân tích các mẫu thức thành nhân tử:

Kiến thức áp dụng

- Để tìm mẫu thức chung của nhiều phân thức ta cần:

+ Phân tích các mẫu thức đã cho thành nhân tử

+ Chọn mẫu thức chung là tích của các nhân tử số và các biểu thức xuất hiện ở các mẫu riêng , trong đó :

+ Nhân tử bằng số là BCNN của các nhân tử bằng số ở các mẫu riêng.

+ Với các biểu thức, lấy biểu thức có số mũ cao nhất.

Câu 5:

Qui đồng mẫu thức các phân thức sau(có thể áp dụng qui tắc đổi dấu với các phân thức để tìm mẫu thức chung thuận tiện hơn):

$a) \frac{4 x^{2} - 3 x + 5}{x^{3} - 1}; \frac{1 - 2 x}{x^{2} + x + 1}; - 2$

$b) \frac{10}{x + 2}; \frac{5}{2 x - 4}; \frac{1}{6 - 3 x} .$

Xem đáp án

a) + Phân tích mẫu thức thành nhân tử để tìm nhân tử chung:

x³ – 1 = (x – 1)(x² + x + 1)

x² + x + 1 = x² + x + 1

⇒ MTC = (x – 1)(x² + x + 1) = x³ – 1

+ Nhân tử phụ : (Có thể bỏ qua bước này nếu đã quen)

(x³ – 1) : (x³ – 1) = 1

(x³ – 1) :( x² + x + 1) = x - 1

(x³ – 1) : 1 = x³ – 1

+ Quy đồng :

b) Ta có:

+ Phân tích mẫu thức thành nhân tử để tìm MTC

x + 2 = x + 2

2x – 4 = 2.(x – 2)

3x – 6 = 3.(x – 2)

⇒ MTC = 6.(x + 2)(x – 2)

+ Nhân tử phụ: (Có thể bỏ qua bước này nếu đã quen)

6(x + 2)(x – 2) : (x + 2) = 6(x – 2)

6(x + 2)(x – 2) : 2(x – 2) = 3(x + 2)

6(x + 2)(x – 2) : 3(x – 2) = 2(x + 2)

+ Quy đồng:

Kiến thức áp dụng

- Để tìm mẫu thức chung của nhiều phân thức ta cần:

+ Phân tích các mẫu thức đã cho thành nhân tử

+ Chọn mẫu thức chung là tích của các nhân tử số và các biểu thức xuất hiện ở các mẫu riêng , trong đó :

+ Nhân tử bằng số là BCNN của các nhân tử bằng số ở các mẫu riêng.

+ Với các biểu thức, lấy biểu thức có số mũ cao nhất.

Câu 6:

Đố. Cho hai phân thức:

$\frac{5 x^{2}}{x^{3} - 6 x^{2}}; \frac{3 x^{2} + 18 x}{x^{2} - 36}$

Khi quy đồng mẫu thức, bạn Tuấn đã chọn MTC = x²(x – 6)(x + 6), còn bạn Lan bảo rằng: "Quá đơn giản! MTC = x – 6". Đố em biết bạn nào đúng?

Xem đáp án

Cả hai bạn đều làm đúng.

- Bạn Tuấn trực tiếp đi tìm mẫu thức chung theo quy tắc:

x³ – 6x² = x²(x – 6)

x² – 36 = x² – 6² = (x – 6)(x + 6)

MTC = x²(x – 6)(x + 6).

- Bạn Lan rút gọn phân thức trước khi đi tìm mẫu thức chung:

MTC = x – 6

* Nhận xét: Ta nên rút gọn hoàn toàn các phân thức trước khi quy đồng để việc quy đồng ngắn gọn hơn.

Câu 7:

Qui đồng mẫu thức của hai phân thức:

$a) \frac{3 x}{2 x + 4} v à \frac{x + 3}{x^{2} - 4};$

$b) \frac{x + 5}{x^{2} + 4 x + 4} v à \frac{x}{3 x + 6} .$

Xem đáp án

a) + Phân tích mẫu thức thành nhân tử để tìm mẫu thức chung

2x + 4 = 2.(x + 2)

x² – 4 = (x – 2)(x + 2)

⇒ MTC = 2.(x – 2)(x + 2)

+ Nhân tử phụ :

2.(x – 2)(x + 2) : 2(x + 2) = x – 2

2(x – 2)(x + 2) : (x – 2)(x + 2) = 2.

+ Quy đồng :

b) + Phân tích mẫu thức thành nhân tử để tìm MTC:

x² + 4x + 4 = x² + 2.x.2 + 2² = (x + 2)²

3x + 6 = 3.(x + 2)

⇒ MTC = 3.(x + 2)²

+ Nhân tử phụ :

3.(x + 2)² : (x + 2)² = 3

3(x + 2)² : 3(x + 2) = x + 2

+ Quy đồng :

Kiến thức áp dụng

- Để tìm mẫu thức chung của nhiều phân thức ta cần:

+ Phân tích các mẫu thức đã cho thành nhân tử

+ Chọn mẫu thức chung là tích của các nhân tử số và các biểu thức xuất hiện ở các mẫu riêng , trong đó :

+ Nhân tử bằng số là BCNN của các nhân tử bằng số ở các mẫu riêng.

+ Với các biểu thức, lấy biểu thức có số mũ cao nhất.

Câu 8:

Qui đồng mẫu thức các phân thức sau:

$a) \frac{1}{x + 2}; \frac{8}{2 x - x^{2}};$

$b) \frac{1}{x + 2} v à \frac{x^{4}}{x^{2} - 1};$

$c) \frac{x^{3}}{x^{3} - 3 x^{2} y + 3 x y^{2} - y^{3}}; \frac{x}{y^{2} - x y}$

Xem đáp án

a) + Phân tích mẫu thức thành nhân tử để tìm MTC

2x – x² = x.(2 – x)

⇒ MTC = x.(x + 2)(2 – x)

+ Nhân tử phụ :

x.(x + 2)(2 – x) : (x + 2) = x.(2 – x)

x(x + 2)(2 – x) : x(2 – x) = x + 2

+ Quy đồng:

Mẫu thức chung = x² – 1

Quy đồng mẫu thức:

+ Phân tích mẫu thức thành nhân tử:

x³ – 3x²y + 3xy² – y³ = (x – y)³

xy – y² = y.(x – y)

⇒ MTC = y.(x – y)³

+ Nhân tử phụ :

y(x – y)³ : (x – y)³ = y

y(x – y)³ : y(x – y) = (x – y)²

+ Quy đồng :

Kiến thức áp dụng

- Để tìm mẫu thức chung của nhiều phân thức ta cần:

+ Phân tích các mẫu thức đã cho thành nhân tử

+ Chọn mẫu thức chung là tích của các nhân tử số và các biểu thức xuất hiện ở các mẫu riêng , trong đó :

+ Nhân tử bằng số là BCNN của các nhân tử bằng số ở các mẫu riêng.

+ Với các biểu thức, lấy biểu thức có số mũ cao nhất.

Câu 9:

Cho hai phân thức: $\frac{1}{x^{2} + 3 x - 10} v à \frac{x}{x^{2} + 7 x + 10}$

Không dùng cách phân tích các mẫu thức thành nhân tử, hãy chứng tỏ rằng có thể quy đồng mẫu thức hai phân thức này với mẫu thức chung là $x^{3} + 5 x^{2} - 4 x - 20$

Xem đáp án

Để chứng tỏ rằng có thể chọn đa thức: x³ + 5x² – 4x – 20 có thể làm mẫu thức chung ta chỉ cần chứng tỏ rằng nó chia hết cho mẫu thức của mỗi phân thức đã cho.

Thật vậy, ta có:

x³ + 5x² – 4x – 20

= x³ + 3x² – 10x + 2x² + 6x – 20

= x(x² + 3x – 10) + 2(x² + 3x – 10)

= (x + 2)(x² + 3x – 10)

⇒ x³ + 5x² – 4x – 20 chia hết cho x² + 3x – 10

x³ + 5x² – 4x – 20

= x³ + 7x² + 10x – 2x² – 14x – 20

= x(x² + 7x + 10) – 2.(x² + 7x + 10)

= (x – 2)(x² + 7x + 10)

⇒ x³ + 5x² – 4x – 20 chia hết cho x² + 7x + 10

Do đó có thể chọn mẫu thức chung là x³ + 5x² – 4x – 20.