20 câu hỏi trắc nghiệm thuộc Bài tập theo tuần Toán 8 - Tuần 2

$\begin{array}{l} 49 x^{2} - 1 = 0 \\ (7 x - 1) (7 x + 1) = 0 \\ \Rightarrow [\begin{array}{l} 7 x - 1 = 0 \\ 7 x + 1 = 0 \end{array} \Rightarrow [\begin{array}{l} x = \frac{1}{7} \\ x = - \frac{1}{7} \end{array} \end{array}$

Câu 11:

Tìm x biết: ${(2 x - 1)}^{2} - (4 x + 1) (x - 3) = - 3$

Xem đáp án

$\begin{array}{l} {(2 x - 1)}^{2} - (4 x + 1) (x - 3) = - 3 \\ 4 x^{2} - 4 x + 1 - 4 x^{2} + 11 x + 3 = - 3 \\ - 4 x + 11 x = - 3 - 3 - 1 \\ 7 x = - 7 \\ x = - 1 \end{array}$

Câu 12:

Tìm x biết: $9 x (x - 1) - {(3 x - 1)}^{2} = 11$

Xem đáp án

$\begin{array}{l} 9 x (x - 1) - {(3 x - 1)}^{2} = 11 \\ 9 x^{2} - 9 x - 9 x^{2} + 6 x - 1 = 11 \\ - 3 x = 12 \Rightarrow x = - 4 \end{array}$

Câu 13:

Tìm x biết: ${(2 x + 3)}^{2} - {(x - 1)}^{2} = 0$

Xem đáp án

$\begin{array}{l} {(2 x + 3)}^{2} - {(x - 1)}^{2} = 0 \\ [(2 x + 3) - (x - 1)] . [(2 x + 3) + (x - 1)] = 0 \\ (x + 4) (3 x + 2) = 0 \Rightarrow [\begin{array}{l} x + 4 = 0 \\ 3 x + 2 = 0 \end{array} \Rightarrow [\begin{array}{l} x = - 4 \\ x = - \frac{2}{3} \end{array} \end{array}$

Câu 14:

Rút gọn các biểu thức sau:

{(x + y)}^{2} + {(x - y)}^{2} - 2 x^{2}

Xem đáp án

$\begin{array}{l} {(x + y)}^{2} + {(x - y)}^{2} - 2 x^{2} \\ = x^{2} + 2 xy + y^{2} + x^{2} - 2 xy + y^{2} - 2 x^{2} = 2 y^{2} \end{array}$

Câu 15:

Rút gọn các biểu thức sau:

2 (x - y) (x + y) + {(x + y)}^{2} + {(x - y)}^{2}

Xem đáp án

$\begin{array}{l} 2 (x - y) (x + y) + {(x + y)}^{2} + {(x - y)}^{2} \\ = {(x + y + x - y)}^{2} = {(2 x)}^{2} = 4 x^{2} \end{array}$

Câu 16:

Rút gọn các biểu thức sau:

(x - 3) (x + 3) - {(x - 5)}^{2}

Xem đáp án

$\begin{array}{l} (x - 3) (x + 3) - {(x - 5)}^{2} \\ = x^{2} - 9 - x^{2} + 10 x - 25 = 10 x - 34 \end{array}$

Câu 17:

Rút gọn các biểu thức sau:

\begin{array}{l} A = 100^{2} - 99^{2} + 98^{2} - 97^{2} + ...... + 2^{2} - 1^{2} \end{array}

Xem đáp án

$\begin{array}{l} A = 100^{2} - 99^{2} + 98^{2} - 97^{2} + ..... + 2^{2} - 1^{2} \\ = (100 - 99) (100 + 99) + (98 - 97) (98 + 97) + ..... + (2 - 1) (2 + 1) \\ = 199 + 195 + .... + 3 = 5050 \end{array}$

Câu 18:

Rút gọn các biểu thức sau:

B = 3 (2^{2} + 1) (2^{4} + 1) (2^{8} + 1) ....... (2^{64} + 1) + 1

Xem đáp án

$\begin{array}{l} B = 3. (2^{2} + 1) (2^{4} + 1) ..... (2^{64} + 1) + 1 \\ = (2^{2} - 1) (2^{2} + 1) (2^{4} + 1) ..... (2^{64} + 1) + 1 \\ = (2^{4} - 1) (2^{4} + 1) ..... (2^{64} + 1) + 1 \\ = ..... \\ = 2^{128} - 1 + 1 = 2^{128} \end{array}$

Câu 19:

Cho hình thang cân ABCD có AB//CD, AB < CD. Kẻ các đường cao AH, BK. Chứng minh: DH = CK

Xem đáp án

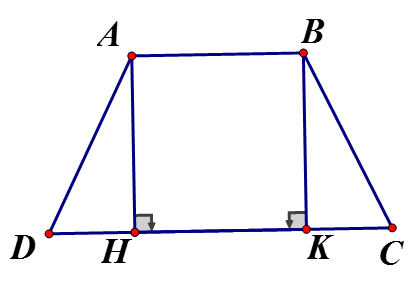
Cho hình thang cân ABCD có AB//CD, AB < CD. Kẻ các đường cao AH, BK (ảnh 1)

Xét $Δ A H D$ vuông tại H và $Δ B K C$ vuông tại K

Có: $A D = B C, \hat{D} = \hat{C}$ (tính chất hình thang cân)

$\Rightarrow Δ A H D = Δ B K C (c h - g n) \Rightarrow D H = C K$ (hai cạnh tương ứng)

Câu 20:

Cho

Δ A B C

cân tại A. Trên các cạnh AB, AC lấy các điểm M, N sao cho BM = CN

a) Tứ giác

B M N C

là hình gì ? Vì sao ?

b) Tính các góc của tứ giác

B M N C

biết

\hat{A} = 40^{0}

Xem đáp án

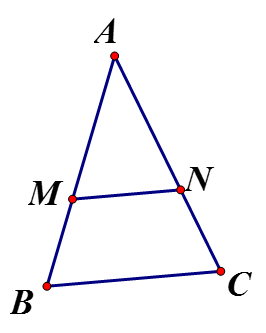
Cho tam giác ABC cân tại A. Trên các cạnh AB, AC lấy các điểm M, N sao cho BM = CN (ảnh 1)

a) Ta có: $A B = A C, B M = N C (g t) \Rightarrow A B - B M = A C - N C \Rightarrow A M = A N \Rightarrow Δ A M N$

cân tại A $\Rightarrow \hat{M} = \frac{180^{0} - \hat{A}}{2} (1)$ mà $Δ A B C$ cân tại $A \Rightarrow B = \frac{180^{0} - \hat{A}}{2} (2)$

Từ (1) và (2) suy ra $\hat{M} = \hat{B}$ mà hai góc ở vị trí đồng vị $\Rightarrow M N / / B C$

Và $\hat{B} = \hat{C}$ (tính chất tam giác cân) $\Rightarrow M N C B$ là hình thang cân

b) Do $\hat{A} = 40^{0} \Rightarrow \hat{B} = \hat{C} = \frac{180^{0} - 40^{0}}{2} = 70^{0}$

Và $\hat{M} = \hat{N} = 180 ° - \hat{B} = 180^{0} - 70^{0} = 110 °$ (tính chất trong cùng phía)

Vậy $\hat{B} = \hat{C} = 40^{0}, \hat{M} = \hat{N} = 110^{0}$

CHỌN BỘ SÁCH BẠN MUỐN XEM

Bài tập cuối tuần Học kì 1 Toán 8 có đáp án

Bài tập theo tuần Toán 8 - Tuần 2

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương