Bài tập theo tuần Toán 8 - Tuần 4
-
6481 lượt thi
-
14 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 12:
Cho hình thang ABCD (AB//CD), M là trung điểm AD, N là trung điểm BC. Gọi I, K lần lượt là giao điểm của MN với BD, AC. Cho biết AB = 6cm, CD = 14cm. Tính độ dài các đoạn thẳng MI, IN, KN.
 Xem đáp án
Xem đáp án
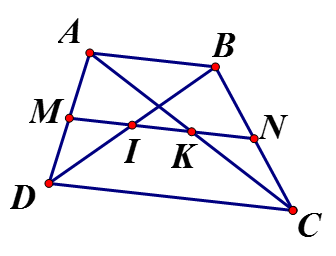
Hình thang ABCD có: M là trung điểm AD, N là trung điểm BC
=> MN là đường trung bình hình thang
có M là trung điểm (do MN//AB mà
=> MI là đường trung bình
Chứng minh tương tự ta có: là đường trung bình
Vậy
Câu 13:
Cho tứ giác ABCD có BC = AD Gọi M, N, P lần lượt là trung điểm AC, CD, DB. Chứng minh cân
 Xem đáp án
Xem đáp án
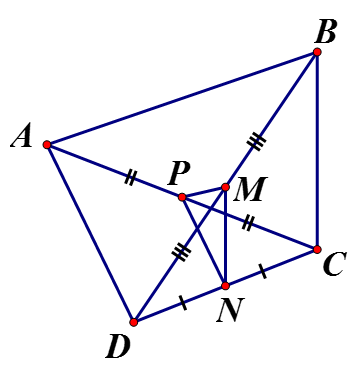
có M là trung điểm AC, N là trung điểm CD => MN là đường trung bình
Chứng minh tương tự là đường trung bình
Mà (3)
Từ (1), (2), (3) cân tại N
Câu 14:
Cho BH là đường cao của Từ trung điểm M của AB, kẻ và từ trung điểm N của cạnh BC kẻ . Chứng minh rằng:
 Xem đáp án
Xem đáp án
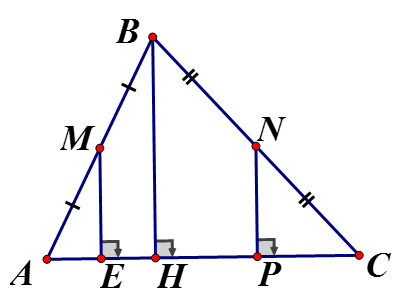
a) Xét có
b) có M là trung điểm là trung đểim AH
=> ME là đường trung bình
Chứng minh tương tự => NP là đường trung bình
và (cùng // BH)
