24 câu hỏi trắc nghiệm thuộc Bài tập theo tuần Toán 8 - Tuần 6

$\begin{array}{l} x^{7} + x^{6} - x - 1 = x^{6} (x + 1) - (x + 1) = (x + 1) (x^{6} - 1) \\ = (x + 1) (x^{3} - 1) (x^{3} + 1) = (x + 1) (x - 1) (x^{2} + x + 1) (x + 1) (x^{2} - x + 1) \\ = {(x + 1)}^{2} (x - 1) (x^{2} - x + 1) (x^{2} + x + 1) \end{array}$

Câu 5:

Phân tích thành nhân tử:

{(x + y)}^{3} - x^{3} - y^{3}

Xem đáp án

$\begin{array}{l} {(x + y)}^{3} - x^{3} - y^{3} = {(x + y)}^{3} - (x^{3} + y^{3}) \\ = (x + y) {(x + y)}^{2} - (x + y) (x^{2} - xy + y^{2}) \\ = (x + y) (x^{2} + 2 xy + y^{2} - x^{2} + xy - y^{2}) = 3 xy (x + y) \end{array}$

Câu 6:

Phân tích thành nhân tử:

x^{3} + 9 x^{2} + 26 x + 24

Xem đáp án

$\begin{array}{l} x^{3} + 9 x^{2} + 26 x + 24 \\ = x^{3} + 3 x^{2} + 6 x^{2} + 18 x + 8 x + 24 \\ = x^{2} (x + 3) + 6 x (x + 3) + 8 (x + 3) \\ = (x + 3) (x^{2} + 6 x + 8) \\ = (x + 3) (x^{2} + 4 x + 2 x + 8) \\ = (x + 3) [x (x + 4) + 2 (x + 4)] = (x + 3) (x + 2) (x + 4) \end{array}$

Câu 7:

Phân tích thành nhân tử:

x^{8} + x + 1

Xem đáp án

$\begin{array}{l} x^{8} + x + 1 = x^{8} - x^{2} + x^{2} + x + 1 \\ = x^{2} (x^{6} - 1) + (x^{2} + x + 1) = x^{2} (x^{3} - 1) (x^{3} + 1) + (x^{2} + x + 1) \\ = x^{2} (x - 1) (x^{2} + x + 1) (x + 1) (x^{2} - x + 1) + (x^{2} + x + 1) \\ = (x^{2} + x + 1) [x^{2} (x - 1) (x + 1) (x^{2} - x + 1) + 1] \end{array}$

Câu 8:

Phân tích thành nhân tử:

(x + 1) (x + 2) (x + 3) (x + 4) - 24

Xem đáp án

$\begin{array}{l} (x + 1) (x + 2) (x + 3) (x + 4) - 24 \\ = [(x + 1) (x + 4) (x + 2) (x + 3)] - 24 \\ = (x^{2} + 5 x + 4) (x^{2} + 5 x + 6) - 24 (*) \end{array} Đặt t = x^{2} + 5 x + 4 \Rightarrow (*) = t (t + 2) - 24 \begin{array}{l} = t^{2} + 2 t - 24 = t^{2} + 6 t - 4 t - 24 = t (t + 6) - 4 (t + 6) \\ = (t + 6) (t - 4) = (x^{2} + 5 x + 4 + 6) (x^{2} + 5 x + 4 - 4) \\ = x (x + 5) (x^{2} + 5 x + 10) \end{array}$

Câu 9:

Phân tích thành nhân tử:

(x + 2) (x + 4) (x + 6) (x + 8) + 16

Xem đáp án

$\begin{array}{l} (x + 2) (x + 4) (x + 6) (x + 8) + 16 \\ = (x + 2) (x + 8) (x + 4) (x + 6) + 16 \\ = (x^{2} + 10 x + 16) (x^{2} + 10 x + 24) + 16 (A) \end{array} Đặt x^{2} + 10 x + 20 = t \begin{array}{l} (A) = (t - 4) (t + 4) + 16 = t^{2} - 16 + 16 \\ = t^{2} = {(x^{2} + 10 x + 20)}^{2} \end{array}$

Câu 10:

Tìm x: $2 (x + 5) - 4 x = 1$

Xem đáp án

$\begin{array}{l} 2 (x + 5) - 4 x = 1 \\ 2 x + 10 - 4 x = 1 \\ - 2 x = - 9 \Rightarrow x = \frac{9}{2} \end{array}$

Câu 11:

Tìm x: $(x - 4) (5 x - 2) - 3 (4 - x) = 0$

Xem đáp án

$\begin{array}{l} (x - 4) (5 x - 2) - 3 (4 - x) = 0 \\ 5 x^{2} - 20 x - 2 x + 8 - 12 + 3 x = 0 \\ 5 x^{2} - 19 x - 4 = 0 \\ 5 x^{2} - 20 x + x - 4 = 0 \\ 5 x (x - 4) + (x - 4) = 0 \\ (x - 4) (5 x + 1) = 0 \Rightarrow [\begin{array}{l} x = 4 \\ x = - \frac{1}{5} \end{array} \end{array}$

Câu 12:

Tìm x: $x^{4} - 8 x^{2} - 9 = 0$

Xem đáp án

$\begin{array}{l} x^{4} - 8 x^{2} - 9 = 0 \Leftrightarrow x^{4} - 9 x^{2} + x^{2} - 9 = 0 \\ \Leftrightarrow x^{2} . (x^{2} - 9) + (x^{2} - 9) \\ \Leftrightarrow (x^{2} + 1) (x^{2} - 9) = 0 \\ \Rightarrow x^{2} - 9 = 0 (do x^{2} + 1 > 0) \\ \Rightarrow [\begin{array}{l} x - 3 = 0 \\ x + 3 = 0 \end{array} \Rightarrow [\begin{array}{l} x = 3 \\ x = - 3 \end{array} \end{array}$

Câu 13:

Tìm x: $x^{3} (3 x - 2) - 8 + 12 x = 0$

Xem đáp án

$\begin{array}{l} x^{3} (3 x - 2) - 8 + 12 x = 0 \\ \Rightarrow x^{3} (3 x - 2) + 4 (3 x - 2) = 0 \\ \Leftrightarrow (3 x - 2) (x^{3} + 4) = 0 \Rightarrow [\begin{array}{l} x = \frac{2}{3} \\ x = \sqrt[3]{- 4} \end{array} \end{array}$

Câu 14:

Tìm x: $5 x (x - 3) - x^{2} + 9 = 0$

Xem đáp án

$\begin{array}{l} 5 x (x - 3) - x^{2} + 9 = 0 \\ 5 x (x - 3) - (x - 3) (x + 3) = 0 \\ \Rightarrow (x - 3) (5 x - x - 3) = 0 \Rightarrow (x - 3) (4 x - 3) = 0 \Rightarrow [\begin{array}{l} x = 3 \\ x = \frac{3}{4} \end{array} \end{array}$

Câu 15:

Tìm x: $x^{2} - 2 x - 24 = 0$

Xem đáp án

$\begin{array}{l} x^{2} - 2 x - 24 = 0 \\ x^{2} - 6 x + 4 x - 24 = 0 \\ x (x - 6) + 4 (x - 6) = 0 \Rightarrow (x + 4) (x - 6) = 0 \\ \Rightarrow [\begin{array}{l} x = - 4 \\ x = 6 \end{array} \end{array}$

Câu 16:

Cho $x + y = 1.$ Tính $A = x^{3} + y^{3} + 3 x y$

Xem đáp án

Cho x + y = 1

$\begin{array}{l} A = x^{3} + y^{3} + 3 xy = (x + y) (x^{2} - xy + y^{2}) + 3 xy \\ = 1. (x^{2} - xy + y^{2}) + 3 xy = x^{2} + 2 xy + y^{2} = {(x + y)}^{2} \end{array}$

Câu 17:

Phân tích đa thức thành nhân tử: $x^{3} - 4 x^{2} + 12 x - 27$

Xem đáp án

$\begin{array}{l} x^{3} - 4 x^{2} + 12 x - 27 = x^{3} - 3 x^{2} - x^{2} + 3 x + 9 x - 27 \\ = x^{2} (x - 3) - x (x - 3) + 9 (x - 3) = (x - 3) (x^{2} - x + 9) \end{array}$

Câu 18:

Phân tích đa thức thành nhân tử:

x^{2} - 2 x - 4 y^{2} - 4 y

Xem đáp án

$\begin{array}{l} x^{2} - 2 x - 4 y^{2} - 4 y = (x^{2} - 4 y^{2}) - (2 x + 4 y) \\ = (x - 2 y) (x + 2 y) - 2 (x + 2 y) = (x + 2 y) (x - 2 y - 2) \end{array}$

Câu 19:

Phân tích đa thức thành nhân tử:

x^{4} + 2 x^{3} - 4 x - 4

Xem đáp án

$\begin{array}{l} x^{4} + 2 x^{3} - 4 x - 4 = x^{4} - 2 x^{2} + 2 x^{3} - 4 x + 2 x^{2} - 4 \\ = x^{2} (x^{2} - 2) + 2 x (x^{2} - 2) + 2 (x^{2} - 2) = (x^{2} - 2) (x^{2} + 2 x + 2) \end{array}$

Câu 20:

Tứ giác ABCD có E, F, G, H theo thứ tự là trung điểm AB, BC, CD, DA. Tứ giác EFGH là hình gì ? Vì sao ?

Xem đáp án

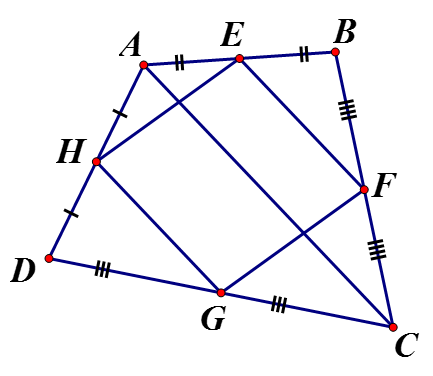
Tứ giác ABCD có E, F, G, H theo thứ tự là trung điểm AB, BC, CD, DA Tứ giác EFGH là hình gì ? Vì sao ? (ảnh 1)

Xét $Δ A D C$ có: H là trung điểm AD, G là trung điểm DC $\Rightarrow G H$ là đường trung bình tam giác $A D C \Rightarrow G H = \frac{1}{2} A C, G H / / A C$ (1)

Cmtt $\Rightarrow E F$ là đường trung bình $Δ A B C \Rightarrow E F = \frac{1}{2} A C, E F / / A C (2)$

Từ (1) và (2) ta có:

\{\begin{cases} E F = G H \\ E F / / G H \end{cases} \Rightarrow E F G H

là hình bình hành.

Câu 21:

Cho hình bình hành ABCD. Các đường chéo cắt nhau tại O. Gọi E, F theo thứ tự là trung điểm của OD, OB. Gọi K là giao điểm của AE và CD. Chứng minh rằng:

a) A E / / C F b) D K = \frac{1}{2} K C

Xem đáp án

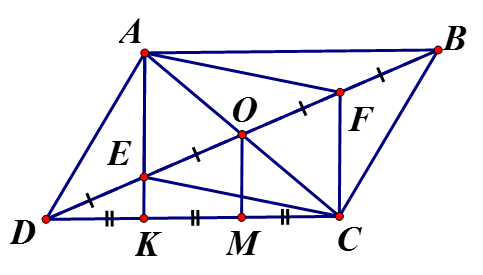
Cho hình bình hành ABCD Các đường chéo cắt nhau tại O. Gọi E, F theo thứ tự là trung điểm của OD, OB. (ảnh 1)

a) Ta có $O D = O B$ mà E, F là trung điểm $O D, O B \Rightarrow O E = O F$

Tứ giác AFCE có $O E = O F, O A = O C \Rightarrow A E C F$ là hình bình hành nên $A E / / C F$

b) Gọi M là trung điểm KC (1)

Xét $Δ A K C$ có O là trung điểm AC (tính chất hình bình hành), M là trung điểm KC (vẽ thêm) => OM là đường trung bình $Δ A K C$ => OM//AK mà $E \in K A \Rightarrow K E / / O M$

Xét $Δ D M O$ có E là trung điểm của OD, $K E / / O M (c m t) \Rightarrow K$ là trung điểm DM $\Rightarrow D K = K M (2)$

Từ (1) và (2) suy ra $D K = K M = M C$ hay $D K = \frac{1}{2} K C$

Câu 22:

Trên đường chéo AC của hình bình hành ABCD lấy hai điểm M và N sao cho AM=CN. Chứng mnh rằng tứ giác BMND là hình bình hành.

Xem đáp án

Trường hợp 1: M nằm giữa O và A

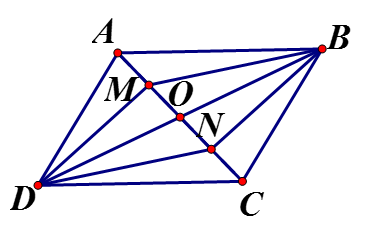
Trên đường chéo AC của hình bình hành ABCD lấy hai điểm M và N sao cho AM = CN (ảnh 1)

Gọi $B D \cap A C = O$

$\Rightarrow O$ là trung điểm AC mà $A M = N C \Rightarrow O M = O N$

Xét tứ giác MBND có: O là trung điểm $M N (c m t); O$ là trung điểm BD (gt)

Nên $B M D N$ là hình bình hành

Trường hợp 2: O nằm giữa A và M

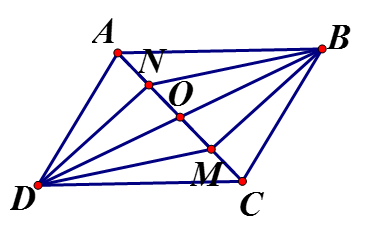
Trên đường chéo AC của hình bình hành ABCD lấy hai điểm M và N sao cho AM = CN (ảnh 2)

$O = A C \cap B D$

Ta có: $O A = O B$ (tính chất hình bình hành) mà

$A M = C N \Rightarrow A M - A O = C N - C O \Rightarrow O M = O N$

Tứ giác $B N D M$ có hai đường chéo $M N, B D$ cắt nhau tại trung điểm O mỗi đường nên $B N D M$ là hình bình hành.

Câu 23:

Cho

Δ A B D,

trên tia đối của tia BA lấy điểm M, trên tia đối của tia DA lấy điểm N sao cho

B M = N D = B D, M D

cắt BN tại I. Dựng hình bình hành ABCD. Gọi K là giao điểm của CI và AD. Chứng minh rằng:

a) CI song song với phân giác của

\hat{A}

b)

A B = D K

Xem đáp án

cho tam giác abc trên tia đối của tia ba lấy điểm M, trên tia đối của tia da lấy điểm N sao cho bm=nd=bd, md cắt bn tại I (ảnh 1)

a) $Δ B M D$ cân do $B M = B D \Rightarrow \hat{M} = \hat{D_{2}}$ mà $\hat{M} = \hat{D_{1}}$ (so le trong) nên $\hat{D_{1}} = \hat{D_{2}} \Rightarrow I D$ là tia phân giác $\hat{B D C}$

Chứng minh tương tự BI là phân giác $\hat{C B D} \Rightarrow I$ là giao điểm 3 đường phân giác

$\Rightarrow C I$ là phân giác $\hat{B C D} .$ Vẽ phân giác Ax của $\hat{A}$

$\Rightarrow \hat{x A D} = \hat{B C K}$ (do $A D C B$ là hình bình hành $\Rightarrow \hat{A} = \hat{C}) \Rightarrow A K = C O \Rightarrow A K C O$ là hình bình hành $\Rightarrow C I / / A O$

b) $Δ D K C$ cân do $\hat{K C D} = \hat{C K D} \Rightarrow C D = C K$ mà $C D = A B \Rightarrow A B = C K$

Câu 24:

Phân tích đa thức thành nhân tử:

ab (a + b) - bc (b + c) + ac (a - c)

Xem đáp án

$\begin{array}{l} ab (a + b) - bc (b + c) + ac (a - c) \\ = a^{2} b + {ab}^{2} - b^{2} c - {bc}^{2} + a^{2} c - {ac}^{2} \\ = ({ab}^{2} - b^{2} c) + (a^{2} b - {bc}^{2}) + ac (a - c) \\ = b^{2} (a - c) + b (a - c) (a + c) + ac (a - c) \\ = (a - c) (b^{2} + ab + bc + ac) \\ = (a - c) [b (a + b) + c (a + b)] = (a - c) (a + b) (b + c) \end{array}$

CHỌN BỘ SÁCH BẠN MUỐN XEM

Bài tập cuối tuần Học kì 1 Toán 8 có đáp án

Bài tập theo tuần Toán 8 - Tuần 6

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương