Bài tập theo tuần Toán 8 - Tuần 14
-
6495 lượt thi
-
15 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 14:
Tính số đo mỗi góc của hình lục giác đều
 Xem đáp án
Xem đáp án
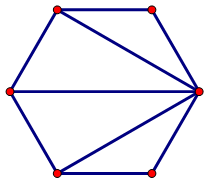
Ta chia lục giác đều ra được 4 tam giác
Suy ra số đo mỗi góc là:
Câu 15:
Cho hình thoi ABCD có Gọi lần lượt là trung điểm Chứng minh EBFGDH là lục giác đều.
 Xem đáp án
Xem đáp án
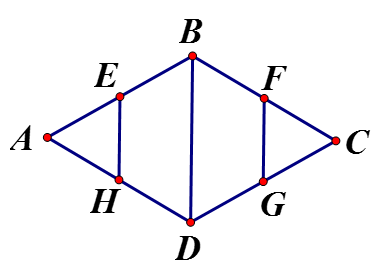
đều do AB = AC và đều (cùng bằng EA)
Chứng minh tương tự:
Lại có tương tự:
Từ (1) và (2)
là lục giác đều.
