29 câu hỏi trắc nghiệm thuộc Bài tập theo tuần Toán 8 - Tuần 5

$\begin{array}{l} x + 1 = {(x + 1)}^{2} \\ (x + 1) - {(x + 1)}^{2} = 0 \\ (x + 1) (1 - x - 1) = 0 \\ - x (x + 1) = 0 \Rightarrow [\begin{array}{l} x = 0 \\ x = - 1 \end{array} \end{array}$

Câu 13:

Tìm x biết: $x^{3} + x = 0$

Xem đáp án

$\begin{array}{l} x^{3} + x = 0 \\ \Rightarrow x (x^{2} + 1) = 0 \\ \Rightarrow x = 0 (do x^{2} + 1 > 0) \end{array}$

Câu 14:

Tìm x biết: $x^{2} - 10 x = - 25$

Xem đáp án

$\begin{array}{l} x^{2} - 10 x = - 25 \\ x^{2} - 10 x + 25 = 0 \\ {(x - 5)}^{2} = 0 \Rightarrow x - 5 = 0 \\ \Rightarrow x = 5 \end{array}$

Câu 15:

Tìm x biết: $x^{3} - 4 x = 0$

Xem đáp án

$\begin{array}{l} x^{3} - 4 x = 0 \Rightarrow x (x^{2} - 4) = 0 \\ \Rightarrow x (x - 2) (x + 2) = 0 \\ \Rightarrow [\begin{array}{l} x = 0 \\ x = 2 \\ x = - 2 \end{array} \end{array}$

Câu 16:

Tìm x biết: $x^{2} (3 x - 2) - 8 + 12 x = 0$

Xem đáp án

$\begin{array}{l} x^{2} (3 x - 2) - 8 + 12 x = 0 \\ x^{2} (3 x - 2) + 4 (3 x - 2) = 0 \\ (3 x - 2) (x^{2} + 4) = 0 \\ \Rightarrow 3 x - 2 = 0 (do x^{2} + 4 > 0) \\ \Rightarrow x = \frac{2}{3} \end{array}$

Câu 17:

Tìm x biết: $2018 x^{2} + x - 2019 = 0$

Xem đáp án

$\begin{array}{l} 2018 x^{2} + x - 2019 = 0 \\ 2018 x^{2} - 2018 x + 2019 x - 2019 = 0 \\ 2018 x (x - 1) + 2019 (x - 1) = 0 \\ (x - 1) (2018 x + 2019) = 0 \\ \Leftrightarrow [\begin{array}{l} x = 1 \\ x = - \frac{2019}{2019} \end{array} \end{array}$

Câu 18:

Chứng minh: $x^{2} + y^{2} + 1 - 2 xy > 0$

Xem đáp án

$\begin{array}{l} x^{2} + y^{2} + 1 - 2 xy \\ = (x^{2} - 2 xy + y^{2}) + 1 \\ = {(x - y)}^{2} + 1 \end{array}$

Vì ${(x - y)}^{2} \geq 0$ (với mọi $x, y) \Rightarrow {(x - y)}^{2} + 1 > 0$ (với mọi $x, y) dfcm$

Câu 19:

Chứng minh: $n^{2} (n + 1) + 2 n (n + 1)$ luôn chia hết cho 6 với mọi $n \in ℤ$

Xem đáp án

$\begin{array}{l} n^{2} (n + 1) + 2 n (n + 1) \\ = (n + 1) (n^{2} + 2 n) = n (n + 1) (n + 2) \end{array}$

Trong ba số liên tiếp luôn tồn tại một số chia hết cho 2, một số chia hết cho 3 mà 2,3 là các số nguyên tố cùng nhau nên

n (n + 1) (n + 2) ⋮ 6 (dfcm)

Câu 20:

Phân tích đa thức thành nhân tử: ${(x + y)}^{2} - {(x - y)}^{2}$

Xem đáp án

$\begin{array}{l} {(x + y)}^{2} - {(x - y)}^{2} \\ = (x + y + x - y) (x + y - x + y) \\ = 2 x . 2 y = 4 xy \end{array}$

Câu 21:

Phân tích đa thức thành nhân tử:

x^{3} + y^{3} + z^{3} - 3 xyz

Xem đáp án

$\begin{array}{l} x^{3} + y^{3} + z^{3} - 3 xyz \\ = {(x + y)}^{3} - 3 xy (x + y) + z^{3} - 3 xyz \\ = [{(x + y)}^{3} + z^{3}] - [3 xy (x + y) + 3 xyz] \\ = (x + y + z) [{(x + y)}^{3} - (x + y) z + z^{2}] - 3 xy (x + y + z) \\ = (x + y + z) (x^{2} + 2 xy + y^{2} - xz - yz + z^{2} - 3 xy) \\ = (x + y + z) (x^{2} + y^{2} + z^{2} - xy - xz - yz) \end{array}$

Câu 22:

Phân tích đa thức thành nhân tử:

ma + mb - a - b

Xem đáp án

$ma + mb - a - b = m (a + b) - (a + b) = (a + b) (m - 1)$

Câu 23:

Cho tam giác ABC cân tại A, đường cao AH. Trên cạnh AB lấy điểm I, trên cạnh AC lấy điểm K sao cho AI = AK. Chứng minh rằng điểm I đối xứng với K qua AH

Xem đáp án

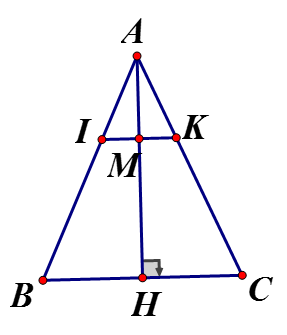
Cho tam giác ABC cân tại A đường cao AH Trên cạnh AB lấy điểm I, trên cạnh AC lấy điểm K sao cho AI = AK (ảnh 1)

Vì $A I = A K \Rightarrow Δ A I K$ cân tại A $\Rightarrow \hat{I} = \frac{180^{0} - \hat{A}}{2}$ và $Δ A B C$ cân (gt)

$\Rightarrow \hat{B} = \frac{180^{0} - \hat{A}}{2} \Rightarrow \hat{I} = \hat{B}$ mà hai góc ở vị trí đồng vị nên $I K / / B C$

Do $A H ⊥ B C \Rightarrow A M ⊥ I K (M = A H \cap I K) (1)$

Ta có: $Δ A I K$ cân tại I có $A M ⊥ I K$

=> AM còn là đường trung tuyến => M là trung điểm IK => MI = MK (2)

Từ (1) và (2) suy ra $\{\begin{cases} A M ⊥ I K \\ I M = I K \end{cases} \Rightarrow I, K$ đối xứng qua AH

Câu 24:

Cho

ΔABC

có

\hat{A} = 60^{0},

trực tâm H. Gọi M là điểm đối xứng với H qua BC

a) Chứng minh

ΔBHC = ΔBMC

b) Tính

\hat{BMC}

Xem đáp án

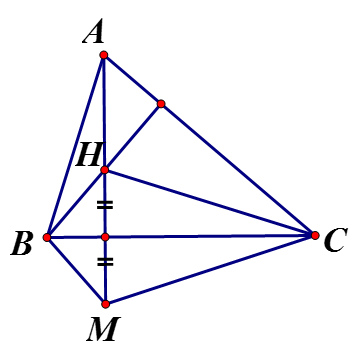
cho tam giác abc có góc a = 60 độ, trực tâm H. Gọi m là điểm đối xứng với h qua bc (ảnh 1)

a) Do $H, M$ đối xứng qua $B C \Rightarrow B C$ là đường trung trực $H M \Rightarrow \{\begin{cases} B H = B M \\ C H = C M \end{cases}$

Xét $Δ B H C$ và $Δ B M C$ có:

$B H = B M, H C = M C (c m t); B C chung \Rightarrow ΔBHC = ΔBMC (c . c . c)$

b) Ta có: $\hat{A B H} = 90^{0} - \hat{B A C}$ (do phụ nhau)

$\hat{C A H} = 90^{0} - \hat{B A C}$ (phụ nhau)

$Δ A B H$ có $\hat{B H M}$ là góc ngoài nên $\hat{B H M} = \hat{B A M} + \hat{A B H}$

cmtt $\Rightarrow \hat{C H M} = \hat{H A C} + \hat{H C A}$

$\begin{array}{l} \Rightarrow \hat{B H C} = \hat{B H M} + \hat{C H M} = \hat{H A C} + \hat{C A H} + \hat{H A B} + \hat{A B H} \\ = \hat{B A C} + 90^{0} - \hat{B A C} + 90^{0} - \hat{B A C} \\ = 180^{0} - \hat{B A C} = 180^{0} - 60^{0} = 120^{0} \end{array}$

Vì $Δ B H C = Δ B M C \Rightarrow \hat{B M C} = \hat{B H C} = 120^{0}$

Câu 25:

Phân tích các đa thức sau thành nhân tử:

2 x^{8} - 12 x^{4} + 18

Xem đáp án

$\begin{array}{l} 2 x^{8} - 12 x^{4} + 18 \\ = 2 (x^{8} - 6 x^{4} + 9) = 2 [{(x^{4})}^{2} - 2 x^{4} . 3 + 3^{2}] = 2 {(x^{4} - 3)}^{2} \end{array}$

Câu 26:

Phân tích đa thức thành nhân tử:

x^{8} + x^{7} + 1

Xem đáp án

$\begin{array}{l} x^{8} + x^{7} + 1 = (x^{8} - x^{2}) + (x^{7} - x) + x^{2} + x + 1 \\ = x^{2} (x^{6} - 1) + x (x^{6} - 1) + x^{2} + x + 1 \\ = x (x + 1) (x^{6} - 1) + (x^{2} + x + 1) \\ = x (x + 1) (x^{3} - 1) (x^{3} + 1) + (x^{2} + x + 1) \\ = x (x + 1) [(x - 1) (x^{3} + 1)] (x^{2} + x + 1) + (x^{2} + x + 1) \\ = (x^{2} + x + 1) [x (x + 1) (x - 1) (x^{3} + 1) + 1] \end{array}$

Câu 27:

Phân tích đa thức sau thành nhân tử:

a^{4} b + 6 a^{2} b^{3} + 9 b^{5}

Xem đáp án

$\begin{array}{l} a^{4} b + 6 a^{2} b^{3} + 9 b^{5} \\ = b (a^{4} + 6 a^{2} b^{2} + 9 b^{4}) = b [{(a^{2})}^{2} + 2 a^{2} . 3 b^{2} + {(3 b^{2})}^{2}] \\ = b {(a + 3 b^{2})}^{2} \end{array}$

Câu 28:

Phân tích đa thức sau thành nhân tử:

mx + my + 5 x + 5 y

Xem đáp án

$\begin{array}{l} mx + my + 5 x + 5 y = m (x + y) + 5 (x + y) \\ = (m + 5) (x + y) \end{array}$

Câu 29:

Phân tích đa thức sau thành nhân tử:

a (a - b) (a + b) - (a + b) (a^{2} - ab + b^{2})

Xem đáp án

$\begin{array}{l} a (a - b) (a + b) - (a + b) (a^{2} - ab + b^{2}) \\ = (a + b) [a^{2} - ab - a^{2} + ab + b^{2}] \\ = b^{2} (a + b) \end{array}$

CHỌN BỘ SÁCH BẠN MUỐN XEM

Bài tập cuối tuần Học kì 1 Toán 8 có đáp án

Bài tập theo tuần Toán 8 - Tuần 5

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương