Bài tập theo tuần Toán 9 - Tuần 25
-
663 lượt thi
-
15 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 3:
Cho parabol và
a) Vẽ (P) và (d) trên cùng một hệ trục tọa độ
b) Tìm tọa độ giao điểm của (P) và (d)
 Xem đáp án
Xem đáp án
a) Học sinh tự vẽ (P) và (d)
b) Ta có phương trình hoành độ giao điểm:
Vậy tọa độ giao điểm
Câu 4:
Cho hàm số có đồ thị là parabol (P)
a) Tìm hệ số a biết rằng (P) đi qua điểm M(-2; 4)
b) Viết phương trình đường thẳng d đi qua gốc tọa độ và điểm N(2; 4)
c) Tìm tọa độ giao điểm của (P) và (d)
 Xem đáp án
Xem đáp án
a) Vì (P) đi qua thay vào (P):
b) (d) đi qua O(0; 0) nên có dạng y = ax và qua
. Vậy phương trình cần tìm y = 2x
c) nên ta có phương trình hoành độ giao điểm . Vậy tọa độ (P) và (d) là
Câu 5:
Cho hàm số với
Tìm các giá trị của tham số m để đồ thị hàm số đi qua điểm với là nghiệm của hệ phương trình :
 Xem đáp án
Xem đáp án
Vì là nghiệm hệ . Thay M(2; 1) vào (d)
Câu 6:
Sau 2 giây vật cách mặt đất bao nhiêu mét
Sau bao lâu vật tiếp đất
 Xem đáp án
Xem đáp án
a) đường di chuyển của vật sau 2 giây: , lúc đó vật cách mặt đất: 100 - 16 = 84 (m)
b) Vật cách mặt đất sau 5 giây do
Câu 7:
Cho điểm A nằm ngoài (O) qua A kẻ hai tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm). Chứng minh tứ giác ABBOC nội tiếp
 Xem đáp án
Xem đáp án
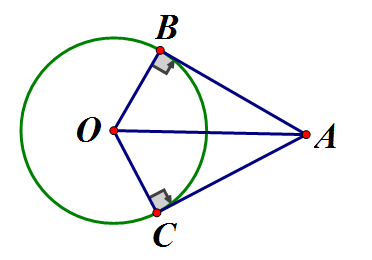
Vì AB, AC là hai tiếp tuyến nên là tứ giác nội tiếp
Câu 8:
Cho hàm số có đồ thị là (P)
a) Vẽ (P) trên hệ trục tọa độ
b) Dựa vào đồ thị, biện luận số nghiệm của phương trình theo m
 Xem đáp án
Xem đáp án
a) Học sinh tự vẽ Parabol
b)
Khi thì phương trình vô nghiệm
Khi phương trình có 1 nghiệm
Khi có hai nghiệm
Câu 9:
Cho đường tròn (O) đường kính AB. Gọi H là điểm nằm giữa O và B. Kẻ dây CD vuông góc với AB tại H. Trên cung nhỏ AC lấy điểm E, kẻ tại K. Đường thẳng DE cắt CK tại F. Chứng minh:
a) AHCK là tứ giác nội tiếp cân
 Xem đáp án
Xem đáp án
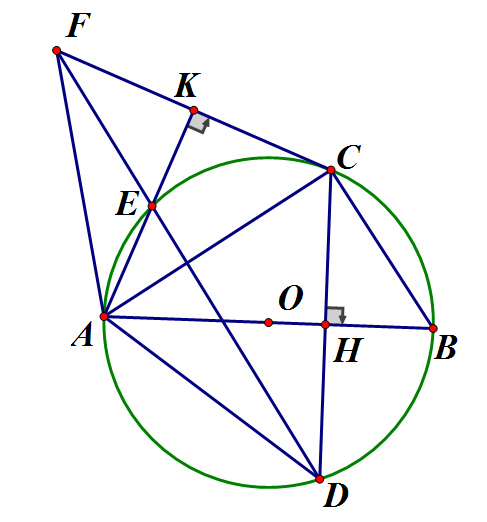
b) vuông tại D, DH đường cao
c) (do AKCH là tứ giác nội tiếp)
(H là trung điểm DC nên K là trung điểm FC)
là tam giác cânCâu 10:
Cho tam giác ABC vuông tại A. Đường tròn (O) đường kính AB cắt BC tại M.
a) Chứng minh và
b) Gọi I là trung điểm của AC. Đường thẳng BI cắt đường tròn (O) tại điểm thứ hai là N. Chứng minh MNCI là tứ giác nội tiếp
Chứng minh
 Xem đáp án
Xem đáp án
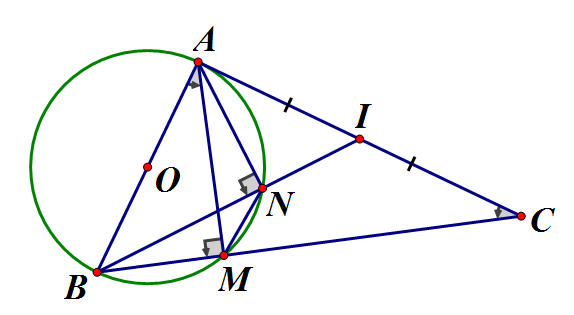
Ta có: (góc nội tiếp chắn nửa đường tròn)
Ta có vuông tại A, AM là đường cao (hệ thức lượng)
Ta có (cùng chắn cung BM)
Mà (cùng phụ )
là tứ giác nội tiếp
Ta có: (góc nội tiếp chắn nửa đường tròn)
Xét và có: chung
Mà AI = IC (gt)
Câu 11:
Cho nửa đường tròn (O), đường kính AB. Kẻ tiếp tuyến Bx với nửa đường tròn. Gọi C là điểm trên nửa đường tròn sao cho cung CA bằng cung CB, D là điểm tùy ý trên cung , các tia AC, AD cắt tia Bx theo thứ tự ở E và F
a) Tính số đo
b) Chứng minh tứ giác CDFE nội tiếp
c) Chứng minh
 Xem đáp án
Xem đáp án
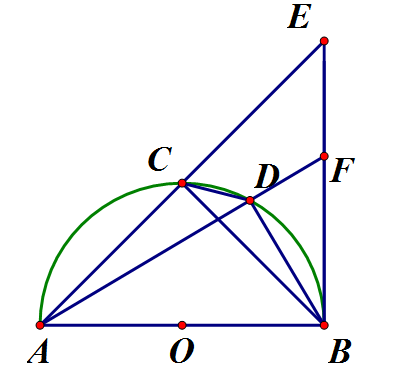
a) Ta có vuông tại B do Bx là tiếp tuyến mà (góc nội tiếp chắn cung vuông cân tại B
b) Ta có . Tứ giác CDFE có là tứ giác nội tiếp
c) Vì vuông tại B, BD đường cao do
(do vuông cân)Câu 12:
Cho nửa đường tròn (O) đường kính BC = 2a. A là điểm trên nửa đường tròn, Đường tròn đường kính AB cắt BC ở D (D khác B), tiếp tuyến của (O) tại D cắt AC tại I. Vẽ
a) Tính theo
b) Chứng minh BEFC là tứ giác nội tiếp
c) Tính
d) Chứng minh rằng : DI là đường trung bình . Tính khi DI // EF
 Xem đáp án
Xem đáp án
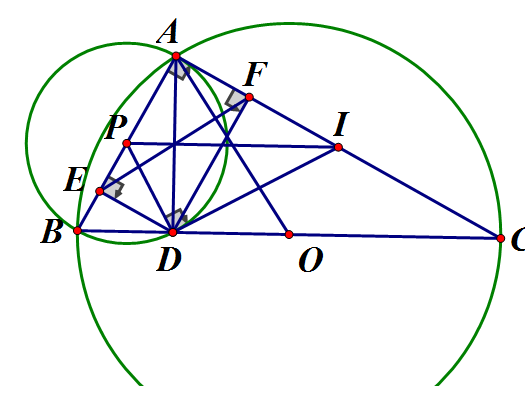
a) Ta có: (góc nội tiếp và góc ở tâm cùng chắn cung AB)
b) Ta có (góc nội tiếp chắn nửa đường tròn)
Chứng minh tương tự
Ta có: là hình chữ nhật
Mà (cùng phụ
là tứ giác nội tiếp
c)
vuông tại D
d) Gọi P là tâm đường tròn đường kính AB
Xét và có: chung
vuông tại D mà cân tại I.
cân tại I
Từ (1) và (2) là đường trung tuyến
Khi DI // EF (So le trong)
Mà ta có
Mà (Tính chất hình chữ nhật)
mà
Câu 13:
Cho nội tiếp (O). Vẽ Ax là tiếp tuyến của đường tròn (O). Đường thẳng song song với Ax cắt cạnh AB, AC lần lượt ở D, E. Chứng minh tứ giác BCED nội tiếp.
 Xem đáp án
Xem đáp án
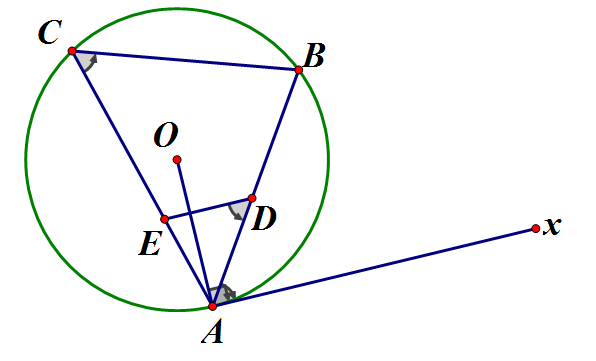
Ta có (cùng chắn mà (so le trong)
Nên là tứ giác nội tiếp
Câu 14:
Cho tứ giác ABCD nội tiếp (O) và AB = BD tiếp tuyến của (O) tại A cắt đường thẳng BC tại Q. Gọi R là giao điểm của hai đường thẳng AB, DC
a) Chứng minh tứ giác AQRC nội tiếp
b) Chứng minh AD // QK
 Xem đáp án
Xem đáp án

a) Ta có: là tứ giác nội tiếp)
(tiếp tuyến – dây cung) (tc góc nội tiếp )
Mà là tứ giác nội tiếp
b) Ta có: là tứ giác nội tiếp)
Và (hệ quả góc nội tiếp) nên
Câu 15:
Cho hình vuông cắt BC và BD lần lượt tại E và F. Ay cắt CD, BD tại G, H. Chứng minh tứ giác EFGH nội tiếp.
 Xem đáp án
Xem đáp án

ABCD là hình vuông nên , lại có ở cùng phía của GF nên A, D nằm trên cung chứa góc , vẽ trên đoạn là tứ giác nội tiếp, có nên AG là đường kính của đường tròn (ADGH). Vì vậy hay là tứ giác nội tiếp.
