27 câu hỏi trắc nghiệm thuộc Bài tập theo tuần Toán 9 - Tuần 21

Câu 1:

Giải hệ phương trình bằng phương pháp cộng đại số:

$\{\begin{cases} 3 x + y = 3 \\ 3 x - y = - 3 \end{cases}$

$\{\begin{cases} 3 x + y = 3 \\ 3 x - y = - 3 \end{cases} \Leftrightarrow \{\begin{cases} 6 x = 0 \\ y = 3 - 3 x \end{cases} \Leftrightarrow \{\begin{cases} x = 0 \\ y = 3 \end{cases}$

Câu 2:

Giải hệ phương trình bằng phương pháp cộng đại số:

$\{\begin{cases} 2 x + 5 y = 8 \\ 2 x - 3 y = 0 \end{cases}$

Xem đáp án

$\{\begin{cases} 2 x + 5 y = 8 \\ 2 x - 3 y = 0 \end{cases} \Leftrightarrow \{\begin{cases} 8 y = 8 \\ x = \frac{3 y}{2} \end{cases} \Leftrightarrow \{\begin{cases} x = \frac{3}{2} \\ y = 1 \end{cases}$

Câu 3:

Giải hệ phương trình bằng phương pháp cộng đại số:

$\{\begin{cases} 4 x + 3 y = 6 \\ 2 x + y = 4 \end{cases}$

Xem đáp án

$\{\begin{cases} 4 x + 3 y = 6 \\ 2 x + y = 4 \end{cases} \Leftrightarrow \{\begin{cases} 4 x + 3 y = 6 \\ 4 x + 2 y = 8 \end{cases} \Leftrightarrow \{\begin{cases} x = 3 \\ y = - 2 \end{cases}$

Câu 4:

Giải hệ phương trình bằng phương pháp cộng đại số:

$\{\begin{cases} 2 x + 3 y = - 2 \\ 3 x - 2 y = - 3 \end{cases}$

Xem đáp án

$\{\begin{cases} 2 x + 3 y = - 2 \\ 3 x - 2 y = - 3 \end{cases} \Leftrightarrow \{\begin{cases} 4 x + 6 y = - 4 \\ 9 x - 6 y = - 9 \end{cases} \Leftrightarrow \{\begin{cases} x = - 1 \\ y = 0 \end{cases}$

Câu 5:

Giải hệ phương trình bằng phương pháp cộng đại số:

$\{\begin{cases} 0, 3 x + 0, 5 y = 3 \\ 1, 5 x - 2 y = 1, 5 \end{cases}$

Xem đáp án

$\{\begin{cases} 0, 3 x + 0, 5 y = 3 \\ 1, 5 x - 2 y = 1, 5 \end{cases} \Leftrightarrow \{\begin{cases} 1, 2 x + 2 y = 12 \\ 45 x - 2 y = 1, 5 \end{cases} \Leftrightarrow \{\begin{cases} x = 5 \\ y = 3 \end{cases}$

Câu 6:

Giải hệ phương trình bằng phương pháp thế:

$\{\begin{cases} x \sqrt{2} - 3 y = 1 \\ 2 x + y \sqrt{2} = - 2 \end{cases}$

Xem đáp án

$\{\begin{cases} x \sqrt{2} - 3 y = 1 \\ 2 x + y \sqrt{2} = - 2 \end{cases} \Leftrightarrow \{\begin{cases} 2 x - 3 \sqrt{2} y = \sqrt{2} \\ 6 x + 3 \sqrt{2} y = - 6 \end{cases} \Leftrightarrow \{\begin{cases} 8 x = \sqrt{2} - 6 \\ y = \frac{- 2 - 2 x}{\sqrt{2}} \end{cases} \Leftrightarrow \{\begin{cases} x = \frac{- 6 + \sqrt{2}}{8} \\ y = - \frac{1 + \sqrt{2}}{4} \end{cases}$

Câu 7:

Giải hệ phương trình bằng phương pháp thế:

$\{\begin{cases} 5 x \sqrt{3} + y = 2 \sqrt{2} \\ x \sqrt{6} - y \sqrt{2} = 2 \end{cases}$

Xem đáp án

$\{\begin{cases} 5 x \sqrt{3} + y = 2 \sqrt{2} \\ x \sqrt{6} - y \sqrt{2} = 2 \end{cases} \Leftrightarrow \{\begin{cases} 5 x \sqrt{6} + y \sqrt{2} = 4 \\ x \sqrt{6} - y \sqrt{2} = 2 \end{cases} \Leftrightarrow \{\begin{cases} x = \frac{\sqrt{6}}{6} \\ y = - \frac{\sqrt{2}}{2} \end{cases}$

Câu 8:

Giải hệ phương trình bằng phương pháp thế:

$\{\begin{cases} - 5 x + 2 y = 4 \\ 6 x - 3 y = - 7 \end{cases}$

Xem đáp án

$\{\begin{cases} - 5 x + 2 y = 4 \\ 6 x - 3 y = - 7 \end{cases} \Leftrightarrow \{\begin{cases} - 15 x + 6 y = 12 \\ 12 x - 6 y = - 14 \end{cases} \Leftrightarrow \{\begin{cases} - 3 x = - 2 \\ y = \frac{4 + 5 x}{2} \end{cases} \Leftrightarrow \{\begin{cases} x = \frac{2}{3} \\ y = \frac{11}{3} \end{cases}$

Câu 9:

Giải hệ phương trình bằng phương pháp thế:

$\{\begin{cases} 2 x - 3 y = 11 \\ - 4 x + 6 y = 5 \end{cases}$

Xem đáp án

$\begin{array}{l} \{\begin{cases} 2 x - 3 y = 11 \\ - 4 x + 6 y = 5 \end{cases} \Leftrightarrow \{\begin{cases} 4 x - 6 y = 22 \\ - 4 x + 6 y = 5 \end{cases} \\ D o \frac{4}{- 4} = \frac{- 6}{6} \neq \frac{22}{5} \Rightarrow P T V N \end{array}$

Câu 10:

Giải hệ phương trình bằng phương pháp thế:

$\{\begin{cases} 3 x - 2 y = 10 \\ x - \frac{2}{3} y = 3 \frac{1}{3} \end{cases}$

Xem đáp án

$\{\begin{cases} 3 x - 2 y = 10 \\ x - \frac{2}{3} y = 3 \frac{1}{3} \end{cases}$

Vì $\frac{3}{1} = \frac{- 2}{\frac{- 2}{3}} = \frac{10}{\frac{10}{3}}$ nên phương trình có vô số nghiệm thỏa $\{\begin{cases} x = t \\ y = \frac{3 t - 10}{2} \end{cases}$

Câu 11:

Giải hệ phương trình bằng phương pháp thế:

$\{\begin{cases} (1 + \sqrt{2}) x + (1 - \sqrt{2}) y = 5 \\ (1 + \sqrt{2}) x + (1 + \sqrt{2}) y = 3 \end{cases}$

Xem đáp án

$\{\begin{cases} (1 + \sqrt{2}) x + (1 - \sqrt{2}) y = 5 \\ (1 + \sqrt{2}) x + (1 + \sqrt{2}) y = 3 \end{cases} \Leftrightarrow \{\begin{cases} - 2 \sqrt{2} y = 2 \\ x = \frac{5 - (1 - \sqrt{2}) y}{1 + \sqrt{2}} \end{cases} \Leftrightarrow \{\begin{cases} x = \frac{- \sqrt{2}}{2} \\ y = \frac{- 6 + 7 \sqrt{2}}{2} \end{cases}$

Câu 12:

Chứng tỏ rằng đường thẳng $(2 m - 5) x + (4 m + 9) y = - 19$ luôn luôn đi qua một điểm cố định .

Xem đáp án

Gọi $M (x_{0}; y_{0})$ là điểm cố định đoạn thẳng đi qua. Ta có:

$\begin{array}{l} (2 m - 5) x_{0} + (4 m + 9) y_{0} = - 19 \\ \Leftrightarrow 2 m x_{0} - 5 x_{0} + 4 m y_{0} + 9 y_{0} = - 19 \\ \Leftrightarrow m (2 x_{o} + 4 y_{0}) = 5 x_{0} - 9 y_{0} - 19 \end{array}$

Với mọi m, phương trình luôn đúng khi $\{\begin{cases} 2 x_{0} + 4 y_{0} = 0 \\ 5 x_{0} - 9 y_{0} = 19 \end{cases} \Leftrightarrow \{\begin{cases} x_{0} = 2 \\ y_{0} = - 1 \end{cases}$

Vậy đường thẳng đã cho luôn đi qua M(2; -1) cố định.

Câu 13:

Cho các điểm $A (2; 5); B (- 1; - 1), C (\frac{1}{2}; 2), D (- 3; 5)$

a) Chứng tỏ rằng A, B, C thẳng hàng

b) Chứng tỏ rằng A, B, D không thẳng hàng

Xem đáp án

a) Gọi đường thẳng $A B : y = m x + n$

Vì $A, B \in$ đường thẳng $A B \Rightarrow \{\begin{cases} 2 m + n = 5 \\ - m + n = - 1 \end{cases} \Leftrightarrow \{\begin{cases} m = 2 \\ n = 1 \end{cases} \Rightarrow A B : y = 2 x + 1$

Ta có: $2 = 2. \frac{1}{2} + 1 \Rightarrow C \in A B \Rightarrow A, B, C$ thẳng hàng.

b) $5 \neq 2. (- 3) + 1 \Rightarrow D \notin A B \Rightarrow A, B, D$ không thẳng hàng.

Câu 14:

Tìm các giá trị của tham số m để nghiệm của hệ phương trình :

$\{\begin{cases} \frac{2 x + 1}{3} - \frac{y + 1}{4} = \frac{4 x - 2 y + 2}{5} \\ \frac{2 x - 3}{4} - \frac{y - 4}{3} = - 2 x + 2 y - 2 \end{cases}$ cũng là nghiệm của phương trình $6 m x - 5 y = 2 m - 4$

Xem đáp án

$\{\begin{cases} \frac{2 x + 1}{3} - \frac{y + 1}{4} = \frac{4 x - 2 y + 5}{5} \\ \frac{2 x - 3}{4} - \frac{y - 4}{3} = - 2 x + 2 y - 2 \end{cases} \Leftrightarrow \{\begin{cases} - \frac{2}{15} x + \frac{3}{20} y = \frac{11}{12} \\ \frac{5}{2} x - \frac{7}{3} y = - \frac{31}{12} \end{cases} \Leftrightarrow \{\begin{cases} x = \frac{97}{38} \\ y = \frac{73}{19} \end{cases}$

Ta có

$6 m x - 5 y = 2 m - 4 h a y 6 m . \frac{97}{38} - 5. \frac{73}{19} = 2 m - 4 \Leftrightarrow m = \frac{289}{253}$

Câu 15:

Cho hệ phương trình $\{\begin{cases} 2 m x + y = 2 \\ 8 x + m y = m + 2 \end{cases}$ (m là tham số)

Giải hệ phương trình khi m = -1

Xem đáp án

Khi m = -1, hệ phương trình thành:

$\{\begin{cases} - 2 x + y = 2 \\ 8 x - y = 1 \end{cases} \Leftrightarrow \{\begin{cases} x = \frac{1}{2} \\ y = 3 \end{cases}$ . Vậy khi $m = - 1 \Rightarrow (x; y) = (\frac{1}{2}; 3)$

Câu 16:

Cho hệ phương trình $\{\begin{cases} 2 m x + y = 2 \\ 8 x + m y = m + 2 \end{cases}$ (m là tham số)

Tìm m để hệ phương trình có nghiệm là $(x, y) = (2; - 6)$

Xem đáp án

Khi phương trình có nghiệm (2; -6) thì

$\{\begin{cases} 4 m - 6 = 2 \\ 16 - 6 m = m + 2 \end{cases} \Leftrightarrow m = 2$

Câu 17:

Giải hệ phương trình sau:

$\{\begin{cases} (x + 3) (y - 5) = x y \\ (x - 2) (y + 5) = x y \end{cases}$

Xem đáp án

$\begin{array}{l} \{\begin{cases} (x + 3) (y - 5) = x y \\ (x - 2) (y + 5) = x y \end{cases} \Leftrightarrow \{\begin{cases} - 5 x + 3 y = 15 \\ 5 x - 2 y = 10 \end{cases} \Leftrightarrow \{\begin{cases} x = 12 \\ y = 25 \end{cases} \end{array}$

Câu 18:

Giải hệ phương trình sau:

$\{\begin{cases} \frac{1}{x} + \frac{1}{y} = \frac{3}{4} \\ \frac{1}{6 x} + \frac{1}{5 y} = \frac{2}{15} \end{cases}$

Xem đáp án

$\{\begin{cases} \frac{1}{x} + \frac{1}{y} = \frac{3}{4} \\ \frac{1}{6 x} + \frac{1}{5 y} = \frac{2}{15} \end{cases}$

Đặt

$a = \frac{1}{x}, b = \frac{1}{y}$ , hệ phương trình thành:

$\{\begin{cases} a + b = \frac{3}{4} \\ \frac{1}{6} a + \frac{1}{5} b = \frac{2}{15} \end{cases} \Leftrightarrow \{\begin{cases} a = \frac{1}{2} \\ b = \frac{1}{4} \end{cases}$

$\Rightarrow \{\begin{cases} x = 2 \\ y = 4 \end{cases}$

Câu 19:

Giải hệ phương trình sau:

$\{\begin{cases} 4 (x + y) = 5 (x - y) \\ \frac{40}{x + y} + \frac{40}{x - y} = 9 \end{cases}$

Xem đáp án

$\begin{array}{l} \{\begin{cases} 4 (x + y) = 5 (x - y) (1) \\ \frac{40}{x + y} + \frac{40}{x - y} = 9 (2) \end{cases} \\ (1) \Rightarrow 4 x + 4 y = 5 x - 5 y \Leftrightarrow x = 9 y \end{array}$

$\Rightarrow (2) \Leftrightarrow \frac{40}{10 y} + \frac{40}{8 y} = 9 \Leftrightarrow y = 1 \Rightarrow (x; y) = (9; 1)$

Câu 20:

Vẽ nửa đường tròn đường kính BC của tam giác đều ABC về phía ngoài của tam giác. Trên đường tròn đó lấy hai điểm D và E sao cho $\overset{⏜}{B D} = \overset{⏜}{D E} = \overset{⏜}{E C}$ . Các tia AD, AE cắt cạnh BC tại M và N. Chứng minh rằng $B M = M N = N C$

Xem đáp án

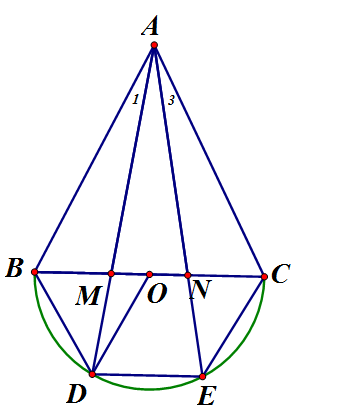
Vẽ nửa đường tròn đường kính BC của tam giác đều ABC về phía ngoài (ảnh 1)

Xét $Δ B A M$ và $Δ C A N$ có: $∠ A_{1} = ∠ A_{3}$ (góc nội tiếp chắn $\overset{⏜}{B D} = \overset{⏜}{C E})$

$∠ B = ∠ C; A B = A C (g t) \Rightarrow Δ B A M = Δ C A N (g . c . g) \Rightarrow B M = C N$

Xét $Δ O B D$ có $O B = O D, ∠ O = 60^{0} \Rightarrow Δ O B D$ đều

$\Rightarrow ∠ D B O = 60^{0} \Rightarrow ∠ D B O = ∠ B C A$ , mà hai góc ở vị trí so le trong nên $B D / / A C \Rightarrow \frac{B M}{C M} = \frac{B D}{B A}$ , mà $\begin{array}{l} B D = B O \\ B A = B C \end{array}\} \Rightarrow \frac{B D}{B A} = \frac{B O}{B C} = \frac{1}{2} \Rightarrow \frac{O D}{A B} = \frac{1}{2}$

Vì $∠ O = ∠ B = 60^{0}$ mà hai góc ở vị trí so le trong nên AB // OD

Áp dụng định lý Ta let ta có $\frac{O M}{M B} = \frac{O D}{A B} = \frac{1}{2},$ Chứng minh tương tự $\Rightarrow \frac{O N}{N C} = \frac{1}{2}$

$\Rightarrow O M + O N = \frac{1}{2} M B + \frac{1}{2} M B = M B (d o M B = N C) \Rightarrow M N = M B$

Vậy

$B M = M N = N C$

Câu 21:

Cho đường tròn tâm O đường kính AB. Vẽ hai dây AM, BN song song với nhau sao cho $s d \overset{⏜}{B M} < 90^{0} .$ Vẽ dây MD song song với AB. Dây DN cắt AB tại E. Từ E vẽ một đường thẳng song song với AM cắt đường thẳng DM tại C. Chứng minh:

a) $A B ⊥ D N$

b) BC là tiếp tuyến của (O)

Xem đáp án

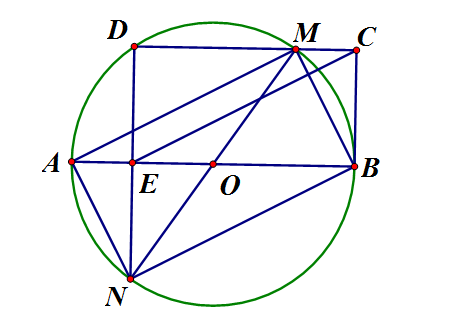
Cho đường tròn tâm O đường kính AB. Vẽ hai dây AM, BN song song với (ảnh 1)

a) Ta có tứ giác AMBN là hình chứ nhật mà O là trung điểm AB nên O là trung điểm $M N \Rightarrow M N$ là đường kính nên $∠ N D M = 90^{0}$

$D N ⊥ A B$ mà $D M / / A B \Rightarrow D N ⊥ A B$

b) Ta chứng minh BCEN là hình bình hành nên BC = EN

Do BCDE là hình bình hành nên $\{\begin{cases} B C = E D \\ D E = E N \end{cases} \Rightarrow \{\begin{cases} B A ⊥ E N \\ B A ⊥ B C \end{cases} \Rightarrow B C$ là tiếp tuyến

Câu 22:

Cho tam giác ABC có AB > AC. Trên cạnh AB lấy một điểm D sao cho AD = AC. Vẽ đường tròn tâm O ngoại tiếp $Δ D B C$ . Từ O lần lượt hạ các đường vuông góc OH, OK xuống BC, BD

a) Chứng minh rằng OH < OK

b) So sánh hai cung nhỏ BD, BC

Xem đáp án

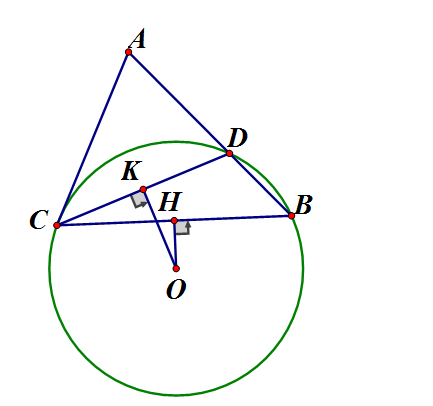
Cho tam giác ABC có AB > AC. Trên cạnh AB lấy một điểm D sao cho AD = AC (ảnh 1)

a) Trong $Δ A B C$ ta có: BC > AB - AC (bất đẳng thức tam giác) mà AC = AD (gt)

$\Rightarrow B C > A B - A D$ hay BC > BD

Trong (O) ta có $B C > B D \Rightarrow O H < O K$ (dây lớn hơn gần tâm hơn)

b) Ta có dây cung $B C > B D \Rightarrow s d \overset{⏜}{B C} > s d \overset{⏜}{B D}$

Câu 23:

Cho đường tròn (O) và hai đường kính AB, CD vuông góc với nhau. Lấy một điểm M trên cung AC rồi vẽ tiếp tuyến đường tròn (O) tại M. Tiếp tuyến này cắt CD tại S. Chứng minh rằng $∠ M S D = 2 ∠ M B A$

Xem đáp án

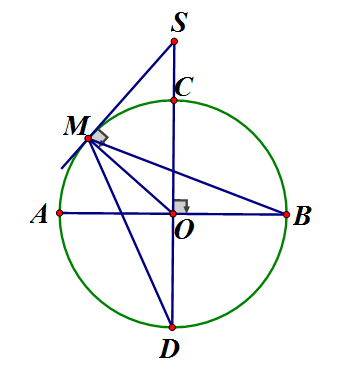
Cho đường tròn (O) và hai đường kính AB, CD vuông góc với nhau. Lấy (ảnh 1)

Ta có $∠ M B A = \frac{1}{2} ∠ M O A$ (góc ở tâm và góc nội tiếp cùng chắn $\overset{⏜}{A B})$

$\Rightarrow ∠ M O A = ∠ M S D$ (cùng phụ $∠ M O S)$

$\Rightarrow ∠ M B A = \frac{1}{2} ∠ M S D$ hay $∠ M S D = 2 ∠ M B A$

Câu 24:

Cho đường tròn (O) và hai dây AB, AC bằng nhau. Qua A vẽ một cát tuyến cắt dây BC ở D và cắt đường tròn (O) ở E. Chứng minh rằng: $A B^{2} = A D . A E$

Xem đáp án

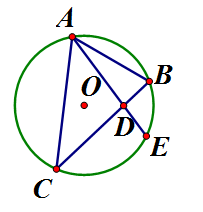
Cho đường tròn (O) và hai dây AB, AC bằng nhau. Qua A vẽ một cát tuyến cắt (ảnh 1)

Ta có: $A B = A C \Rightarrow s d \overset{⏜}{A B} = s d \overset{⏜}{A C} \Rightarrow ∠ A B D = ∠ E$

$Δ A B D$ và $Δ A E B$ có: $∠ A$ chung, $∠ A B D = ∠ E (c m t) \Rightarrow Δ A B D ~ Δ A E B (g - g)$

$\Rightarrow \frac{A B}{A E} = \frac{A D}{A B} \Rightarrow A B^{2} = A D . A E$

Câu 25:

Cho đường tròn (O), đường kính AB điểm D thuộc đường tròn. Gọi E là điểm đối xứng với A qua D.

a) Tam giác ABE là tam giác gì ? Vì sao ?

b) Gọi K là giao điểm của EB với (O). Chứng minh $O D ⊥ A K$

Xem đáp án

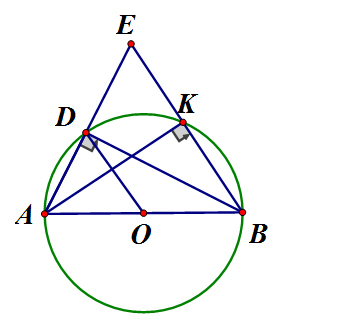
Cho đường tròn (O), đường kính AB điểm D thuộc đường tròn. Gọi E là (ảnh 1)

a) $∠ A D B = 90^{0}$ (góc nội tiếp chắn nửa đường tròn) $\Rightarrow B D ⊥ A E \Rightarrow Δ A B E$ có BD vừa là đường cao vừa là đường trung tuyến nên $Δ A B E$ cân tại B

b) Xét $Δ A B E : D$ là trung điểm AE, O là trung điểm AB nên OD là đường trung bình $Δ A E D \Rightarrow O D / / B E$

Mà $B E ⊥ A K (∠ A K B = 90^{0}$ do là góc bội tiếp chắn nửa đường tròn $\Rightarrow A K ⊥ O D$

Câu 26:

Cho tam giác ABC nội tiếp đường tròn (O), hai đường cao BD, CE cắt nhau tại H. Vẽ đường kính AF.

a) Tứ giác BFCH là hình gì ?

b) Gọi M là trung điểm của BC. Chứng minh rằng 3 điểm H, M, F thẳng hàng.

c) Chứng minh $O M = \frac{1}{2} A H$

Xem đáp án

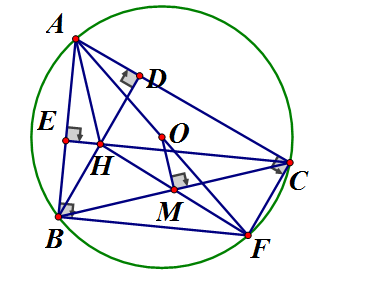
Cho tam giác ABC nội tiếp đường tròn (O), hai đường cao BD, CE cắt nhau tại H. (ảnh 1)

a) Ta có: $∠ A B F = ∠ A C F = 90^{0}$ (góc nội tiếp chắn nửa đường tròn) nên $A B ⊥ B F, A C ⊥ C F$

$* \{\begin{cases} C E ⊥ A B \\ F B ⊥ A B \end{cases} \Rightarrow C H / / B F, * \{\begin{cases} B H ⊥ A C \\ F C ⊥ A C \end{cases} \Rightarrow B H / / F C$ $\Rightarrow B H C F$ là hình bình hành

b) Tứ giác BHFC là hình bình hành mà M là trung điểm BC nên M là trung điểm HF

$\Rightarrow H, M, F$ thẳng hàng.

c) Xét $Δ F H A$ có M là trung điểm HF, O là trung điểm AF

$\Rightarrow O M$ là đường trung bình $Δ F H A \Rightarrow O M = \frac{1}{2} A H$

Câu 27:

Cho nửa đường tròn (O), đường kính AB = 2R và điểm C nằm ngoài nửa đường tròn và cùng phía với nửa mặt phẳng có bờ là đường thẳng AB và chứa nửa đường tròn. Đường thẳng CA cắt nửa đường tròn ở M, CB cắt nửa đường tròn ở N. Gọi H là giao điểm của AN và BM

a) Chứng minh : $C H ⊥ A B$

b) Gọi I là trung điểm CH. Chứng minh MI là tiếp tuyến của nửa đường tròn (O).

Xem đáp án

Cho nửa đường tròn (O), đường kính AB = 2R và điểm C nằm ngoài nửa đường tròn (ảnh 1)

a) $∠ A M B = ∠ A N B = 90^{0}$ (góc nội tiếp chắn nửa đường tròn) $\Rightarrow \{\begin{cases} B M ⊥ A C \\ A N ⊥ B C \end{cases}$

Xét $Δ A B C$ có: $\{\begin{cases} A N ⊥ B C \\ B M ⊥ A C \end{cases} \Rightarrow H$ là trực tâm $\Rightarrow C H ⊥ A B$

b) $Δ C M H$ vuông tại M có MI là trung tuyến $\Rightarrow C I = M I$ $\Rightarrow Δ M C I$ cân nên $∠ C M I = ∠ I C M$

Chứng minh tương tự ta có: $∠ O M A = ∠ O A M \Rightarrow ∠ I M O = 90^{0}$ $\Rightarrow M I ⊥ M O$ mà M thuộc (O) nên MI là tiếp tuyến của (O)

CHỌN BỘ SÁCH BẠN MUỐN XEM

Bài tập theo tuần Toán 9 - Tuần 21

Bài tập theo tuần Toán 9 - Tuần 21

Danh sách câu hỏi

Có thể bạn quan tâm

Các bài thi hot trong chương