Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 1: Đại số)
-
1656 lượt thi
-
188 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
Thay n = 10 vào công thức , ta được:
Vậy số để bạn An bấm vào ổ khóa số mở cửa kho báu là 103
Câu 2:
Vận tốc lăn v (tính bằng m/s) của một vật thể nặng m (tính bằng kg) được tác động một lực Ek (gọi là năng lượng Kinetic Energy, ký hiệu Ek, tính bằng Joule) được cho bởi công thức:
 Xem đáp án
Xem đáp án
a) Thay vào công thức , ta được:
Vậy vận tốc của một quả banh bowling là 3,46m/s
Câu 3:
 Xem đáp án
Xem đáp án
b) Thay vào công thức , ta được:
Vậy cần sử dụng năng lượng Kinetic
Câu 4:
 Xem đáp án
Xem đáp án
a) Thay vào công thức , ta được:
(volt)
Vậy số volt để thắp sáng một bóng đèn A là 104,88 (volt)
Câu 5:
 Xem đáp án
Xem đáp án
b) Thay vào công thức , ta được:
(watt) > 100 (watt)
Vậy bóng đèn B có công suất lớn hơn bóng đèn ACâu 6:
Tốc độ của một chiếc canô và độ dài đường sóng nước để lại sau đuôi của nó được cho bởi công thức . Trong đó, l là độ dài đường nước sau đuôi canô (mét), v là vận tốc canô (m/giây).
a) Một canô đi từ Năm Căn về huyện Đất Mũi (Cà Mau) để lại đường sóng nước sau đuôi dài . Hỏi vận tốc của canô?
 Xem đáp án
Xem đáp án
a Thay vào công thức , ta được:
Câu 7:
 Xem đáp án
Xem đáp án
b) Thay v = 54km/h = 15m/s vào công thức , ta được:
Vậy đường sóng nước để lại sau đuôi chiếc canô dài 9m
Câu 8:
 Xem đáp án
Xem đáp án
a) Thay t = 365 vào công thức , ta được:
(triệu dặm) (triệu km)
Vậy khoảng cách giữa Trái Đất và Mặt Trời 149,3 triệu km
Câu 9:
 Xem đáp án
Xem đáp án
b) Thay t = 687 vào công thức , ta được:
(triệu dặm) (triệu km)
Vậy khoảng cách giữa Sao Hỏa và Mặt Trời 227,6 triệu km
Câu 10:
Sóng thần (tsunami) là một loạt các đợt sóng tạo nên khi một thể tích lớn của nước đại dương bị dịch chuyển chớp nhoáng trên một quy mô lớn. Động đất cùng những dịch chuyển địa chất lớn bên trên hoặc bên dưới mặt nước, núi lửa phun và va chạm thiên thạch đều có khả năng gây ra sóng thần. Cơn sóng thần khởi phát từ dưới đáy biển sâu, khi còn ngoài xa khơi, sóng có biên độ (chiều cao sóng) khá nhỏ nhưng chiều dài của cơn sóng lên đến hàng trăm km. Con sóng đi qua đại dương với tốc độ trung bình 500 dặm một giờ. Khi tiến tới đất liền, đáy biển trở nên nông, con sóng không còn dịch chuyển nhanh được nữa, vì thế nó bắt đầu “dựng đứng lên” có thể đạt chiều cao một tòa nhà sáu tầng hay hơn nữa và tàn phá khủng khiếp.
Tốc độ của con sóng thần và chiều sâu của đại dương liên hệ bởi công thức . Trong đó, , d (deep) là chiều sâu đại dương tính bằng m, s là vận tốc của sóng thần tính bằng m/s. Xem đáp án
Xem đáp án
a) Thay vào công thức , ta được:
Vậy tốc độ trung bình của các con sóng thần là 193m/s
Câu 11:
 Xem đáp án
Xem đáp án
b) Thay s = 220; g = 9,81 vào công thức , ta được:
Vậy độ sâu của đại dương nơi xuất phát con sóng thần này là 4934m
Câu 12:
 Xem đáp án
Xem đáp án
a) Thay vào công thức , ta được:
Vậy bán kính tối thiểu của cung tròn phải là 21,8m.
Câu 13:
 Xem đáp án
Xem đáp án
b) Thay vào công thức , ta được:
Vậy gia tốc tối đa cho phép là 2,56m/s2
Câu 14:
 Xem đáp án
Xem đáp án
Quãng đường vận động viên nhảy từ vị trí A đến vị trí B là:
Thay S = 2000 vào công thức , ta được:
giây
Vậy vận động viên phải mở dù sau thời gian 20,2 giây.
Câu 15:
 Xem đáp án
Xem đáp án
a) Thay x=3 vào công thức , ta được:
Vậy sau 3 giây thì vật nặng còn cách mặt đất là: 55 – 45 = 10m
Câu 16:
b) Khi vật nặng còn cách đất 25m thì nó đã rơi được thời gian bao lâu?
 Xem đáp án
Xem đáp án
b) Quãng đường chuyển động của vật nặng còn cách đất 25m là: 55 – 25 = 30m
Thay vào công thức , ta được:
(giây)
Vậy thời gian vật nặng rơi được là 2,4 giây
Câu 17:
Thời gian t (tính bằng giây) từ khi một người bắt đầu nhảy bungee trên cao cách mặt nước d (tính bằng m) đến khi chạm mặt nước được cho bởi công thức:
a) Tìm thời gian một người nhảy bungee từ vị trí cao cách mặt nước 108m đến khi chạm mặt nước?
 Xem đáp án
Xem đáp án
a) Thay d = 108 vào công thức , ta được:
giây
Vậy thời gian một người nhảy bungee là 5,75 giây
Câu 18:
 Xem đáp án
Xem đáp án
b) Thay t=7 vào công thức , ta được:
Vậy độ cao của người nhảy bungee so với mặt nước là 160,07m
Câu 19:
Do Trái Đất hình cầu nên sự uống cong bề mặt của nó đã ngăn không cho chúng ta nhìn xa quá một khoảng cách nhất định. Cũng vì lý do đó cho nên khi càng lên cao, tầm quan sát của mắt người càng lớn.
Khoảng cách d (tính bằng km) từ một người ở vị trí có chiều cao h (tính bằng mét) nhìn thấy được được chân trời được cho bởi công thức:
 Xem đáp án
Xem đáp án
a) Thay h=65 vào công thức , ta được:
Vậy khoảng cách d từ người đó đến đường chân trời là 28,78km
Câu 20:
 Xem đáp án
Xem đáp án
b) Thay d = 25 vào công thức , ta được:
Vậy vị trí quan sát của ngọn hải đăng phải được xây cao so với mặt nước biển là 49,04m
Câu 21:
Tốc độ tăng trưởng dân số bình quân hàng năm có thể tính theo công thức:
Trong đó:
![]() : Dân số thời điểm gốc
: Dân số thời điểm gốc
![]() : Dân số thời điểm năm sau
: Dân số thời điểm năm sau
![]() : Tốc độ tăng trưởng dân số bình quân hàng năm.
: Tốc độ tăng trưởng dân số bình quân hàng năm.
Tổng số dân Việt Nam năm 2014 là 90728,9 ngàn người. Tổng số dân Việt Nam năm 2015 là: 91703,8 ngàn người.
a) Hãy tính tốc độ tăng trưởng dân số bình quân hàng năm của Việt Nam trong giai đoạn trên.
 Xem đáp án
Xem đáp án
a) Thay vào công thức , ta được:
Vậy tốc độ tăng trưởng dân số bình quân hàng năm trong giai đoạn trên của Việt Nam là 1%
Câu 22:
 Xem đáp án
Xem đáp án
b) Thay vào công thức , ta được:
Vậy ước tính số dân Việt Nam vào năm 2016 là 93547,05 ngàn người
Câu 23:
Để ước tính tốc độ s (dặm/giờ) của một chiếc xe, cảnh sát sử dụng công thức:
(với d (tính bằng feet) là độ dài vết trượt của bánh xe và f là hệ số ma sát).
 Xem đáp án
Xem đáp án
a) Thay f = 0,73 và d = 49,7 vào công thức , ta được:
(dặm/h)(km/h)
Vì nên xe đó vượt quá tốc độ cho phép
Câu 24:
 Xem đáp án
Xem đáp án
b) Quy đổi: 48(km/h)(dặm/h)
Thay ; f = 0,45 vào công thức , ta được:
(feet)
Vậy vết trượt trên nền đường dài 65,82 (feet)
Câu 25:
Số lượng táo trung bình một người châu Mỹ tiêu thụ mỗi năm trong giai đoạn 1980 đến 2000 được biểu diễn bởi công thức: . Trong đó y là số táo mỗi người tiêu thụ trong một năm tính theo pound, x là năm (chạy từ 1980 đến 2000).
a) Hỏi năm 1990 mỗi đầu người tiêu thụ bao nhiêu pound táo?
 Xem đáp án
Xem đáp án
a) Thay vào công thức , ta được:
(pound)
Vậy năm 1990 số lượng táo tiêu thụ là 210 (pound)
Câu 26:
b) Nếu công thức tính số lượng táo tiêu thụ vẫn còn giá trị cho những năm sau thì mỗi người sẽ tiêu thụ 211 pound táo vào năm nào?
(Giá trị quốc tế được công nhận hiện nay là 1 pound = 0,454kg)
 Xem đáp án
Xem đáp án
b) Thay y=211 vào công thức , ta được:
Vậy mỗi người sẽ tiêu thụ 211 pound táo vào năm 2016
Câu 27:
a) Một con hươu cao cổ cân nặng 180kg thì cao bao nhiêu mét?
 Xem đáp án
Xem đáp án
a) Thay x=180 vào công thức , ta được:
Vậy chiều cao của hươu cao cổ là 2,26m
Câu 28:
b) Một con hươu cao cổ có chiều cao 2,56m thì cân nặng bao nhiêu kg?
 Xem đáp án
Xem đáp án
b) Thay h = 2,56 vào công thức , ta được:
Vậy cân nặng của hươu cao cổ là 262,14kg
Câu 29:
Theo quy định, bán kính trái bóng rỗ của nữ nhỏ hơn của nam. Bán kính của trái bóng rổ được cho bởi công thức: . Trong đó, r là bán kính của trái bóng rổ tính bằng inch (1inch = 2,54cm), V là thể tích không khí được chứa trong trái bóng tính bằng inch3).
a) Tính bán kính của trái bóng rổ nữ biết nó chứa được 413 inch3 không khí.
 Xem đáp án
Xem đáp án
a) Thay V = 413 vào công thức , ta được:
(inch)
Vậy bán kính của trái bóng rổ nữ là 4,62 (inch)
Câu 30:
b) Tính thể tích của trái bóng rổ nam biết nó có bán kính 4,77 inch.
 Xem đáp án
Xem đáp án
b) Thay vào công thức , ta được:
(inch3)
Vậy thể tích của trái bóng rổ nam là 454,61 (inch3)
Câu 31:
Địa y là một dạng kết hợp giữa nấm và một loại sinh vật có thể quang hợp (có thể là tảo lục hay khuẩn lam) trong một mối quan hệ cộng sinh. Địa y tồn tại ở một số môi trường khắc nghiệt nhất thế giới đài nguyên bắc cực, sa mạc, bờ đá. Chúng rất phong phú trên các lá và cành cây tại rừng mưa và rừng gỗ, trên đá, cả trên tường gạch và đất. Nóc của nhiều tòa nhà cũng có địa y mọc. Địa y rất phổ biến và có thể sống lâu; tuy nhiên, nhiều loại địa y dễ bị tổn thương khi thay đổi thời tiết đột ngột, chúng có thể được các nhà khoa học dùng để đo mức độ ô nhiễm không khí, hay hủy hoại tầng ôzôn.
Kết quả của sự nóng dần lên của trái đất làm băng tan trên các dòng sông bị đóng băng. Mười hai năm sau khi băng tan, những thực vật nhỏ, được gọi là Địa y, bắt đầu phát triển trên đá. Mỗi nhóm địa y phát triển trên một khoảng đất hình tròn.
Mối quan hệ giữa đường kính d, tính bằng mi-li-mét (mm), của hình tròn và tuổi t của Địa y có thể biểu diễn tương đối theo công thức:
, với
a) Em hãy sử dụng công thức trên để tính đường kính của một nhóm Địa y, 16 năm sau khi băng tan.
 Xem đáp án
Xem đáp án
a) Thay t = 16 vào công thức , ta được:
mm
Vậy sau 16 năm thì đường kính của một nhóm Địa y là 14mm
Câu 32:
 Xem đáp án
Xem đáp án
b) Thay d = 35 vào công thức , ta được:
(năm)
Vậy băng tan cách đó: 37+12=49 (năm)
Câu 33:
Để tính toán thời gian một chu kỳ đong đưa (một chu kỳ đong đưa dây đu được tính từ lúc dây đu bắt đầu được đưa lên cao đến khi dừng hẳn) của một dây đu, người ta sử dụng công thức: . Trong đó, T là thời gian một chu kỳ đong đưa, L là chiều dài của dây đu, g = 9,81m/s2.
a) Một dây đu có chiều dài , hỏi chu kỳ đong đưa dài bao nhiêu giây?
 Xem đáp án
Xem đáp án
a) Thay vào công thức , ta được:
(giây)
Vậy chu kỳ đong đưa dài 3,88 giây
Câu 34:
 Xem đáp án
Xem đáp án
b) Thay vào công thức , ta được:
Vậy phải làm một dây đu dài 4m
Câu 35:
Cho biết các công thức tính sau:
Dân số thành phố A trong năm thứ t là:
(nghìn người)
Tổng thu nhập bình quân của thành phố A trong năm thứ t là:
(triệu USD)
Thu nhập bình quân đầu người của thành phố A trong năm thứ t là: .
a) Hỏi thu nhập bình quân đầu người của thành phố A trong năm 2017 là bao nhiêu? Xem đáp án
Xem đáp án
a) Dân số thành phố A trong năm 2017 là:
(nghìn người)
Quy đổi: 1500 nghìn người = 1500000 người
Tổng thu nhập bình quân của thành phố A trong năm 2017 là:
(triệu USD)
Quy đổi: triệu USD = 13379088,16 USD
Thu nhập bình quân đầu người của thành phố A trong năm 2017 là:
Câu 36:
 Xem đáp án
Xem đáp án
b) Dân số thành phố A trong năm 2020 là:
(nghìn người)
Quy đổi: nghìn người = 1500600 người
Tổng thu nhập bình quân của thành phố năm 2020 là:
(triệu USD)
Quy đổi: triệu USD = 16170961,6 USD
Thu nhập bình quân đầu người của thành phố A trong năm 2020 là:
Câu 37:
Khi cần nâng vật tải trọng nặng phải sử dụng 4 nhánh dây cáp thì sự đồng đều về độ dài dây của các nhánh có ý nghĩa rất quan trọng vì đảm bảo sự phân bố tải trọng lên các nhánh, nếu không sẽ có nhánh chịu vượt tải, mất cân bằng và có khi gây tai nạn. Chiều dài của mỗi nhánh dây được xác định theo công thức:
Trong đó:
L (m) là độ dài của nhánh dây cáp
h (m) là chiều cao tam giác tạo thành bởi các nhánh
b (m) là khoảng cách giữa các điểm cố định dây cáp theo đường chéo
Cần nâng một vật nặng hình vuông, khoảng cách giữa hai điểm cố định trên một cạnh bất kỳ của hình vuông là m. Tính độ dài đường chéo b của vật nặng hình vuông và độ dài dây cáp L, biết khoảng cách từ cù móc đến vật nặng là .
 Xem đáp án
Xem đáp án
Áp dụng định lý Pytago, ta có:
Độ dài đường chéo b của vật nặng hình vuông là 4m
Thay vào công thức , ta được:
Độ dài dây cáp L là (m)
Câu 38:
 Xem đáp án
Xem đáp án
a) Thay y = 256 vào công thức y = 30x + 16, ta được:
30x + 16 = 256
30x = 240
x = 8 (thỏa)
Vậy chim cắt tốn thời gian là 8 giây
Câu 39:
 Xem đáp án
Xem đáp án
b) Thay x = 3 vào công thức , ta được:
Độ cao khi nó bay xuống sau 3 giây là:
Câu 40:
Theo tài liệu dân số và phát triển của Tổng cục dân số và kế hoạch hóa gia đình thì:
Dựa trên số liệu về dân số, kinh tế, xã hội của 85 nước trên thế giới, người ta xây dựng được hàm nêu lên mối quan hệ giữa tuổi thọ trung bình của phụ nữ (y) và tỷ lệ biết chữ của họ (x) như sau: . Trong đó y là số năm (tuổi thọ), x là tỷ lệ phần trăm biết chữ của phụ nữ.
a) Theo báo cáo của Bộ Giáo dục và Đào tạo năm học 2015-2016, tỷ lệ biết chữ đã đạt 96,83% trong nhóm phụ nữ Việt Nam tuổi từ 15 đến 60. Hỏi với tỷ lệ biết chữ của phụ nữ Việt Nam như trên thì nhóm này có tuổi thọ bao nhiêu?
 Xem đáp án
Xem đáp án
a) Thay x = 96,83 vào công thức , ta được:
(năm)
Vậy nhóm này có tuổi thọ 76,89 tuổi
Câu 41:
 Xem đáp án
Xem đáp án
b) Thay y = 77 vào công thức , ta được:
Vậy tỉ lệ biết chữ của họ phải đạt 97,17%
Câu 42:
Để đổi từ nhiệt độ F (Fahrenheit) sang độ C (Celsius), ta dùng công thức sau: .
a) C có phải là hàm số bậc nhất theo biến số F không? Giải thích.
 Xem đáp án
Xem đáp án
Câu 43:
 Xem đáp án
Xem đáp án
b) Thay F = 30 vào công thức , ta được:
Vậy
Câu 44:
 Xem đáp án
Xem đáp án
Ta có:
Biểu thức biểu diễn hàm số bậc nhất F theo biến số C là:
Thay C = 25 vào công thức , ta được:
Vậy
Câu 45:
Giá trị của một chiếc máy tính bảng sau khi sử dụng t năm được cho bởi công thức:
V(t) = 9 800 000 – 1 200 000.t (đồng)
a) Hãy tính V(2) và cho biết V(2) có nghĩa là gì? Xem đáp án
Xem đáp án
a) Thay t = 2 vào công thức V(t) = 9 800 000 – 1 200 000.t, ta được:
V(2) = 9 800 000 – 1 200 000.2 = 7 400 000 (đồng)
Ý nghĩa V(2) là giá tiền của chiếc máy tính bảng sau 2 năm.
Câu 46:
 Xem đáp án
Xem đáp án
b) Thay V(t) = 5 000 000 vào công thức V(t) = 9 800 000 – 1 200 000.t, ta được:
5 000 000 = 9 800 000 – 1 200 000.t
Vậy sau 4 năm, giá của chiếc máy tính bảng là 5 000 000 đồng
Câu 47:
Dưới đây là hình ảnh dấu chân của một người:

Gọi n (bước) là số bước chân trong một phút và p (mét) là khoảng cách giữa hai gót chân liên tiếp. Khi đó hàm số của n theo p sẽ là n = 140.p
a) Hoàng bước được 49 bước trong vòng 1 phút. Hỏi khoảng cách giữa hai gót chân của Hoàng là bao nhiêu?
 Xem đáp án
Xem đáp án
a) Thay n = 49 vào công thức n = 140.p, ta được:
140.p = 49
Vậy khoảng cách giữa hai gót chân của Hoàng là 0,35m
Câu 48:
 Xem đáp án
Xem đáp án
b) Số bước chân của Long trong 1 phút là:
Thay n = 56 vào công thức n = 140.p, ta được:
140.p = 56
Vậy khoảng cách giữa hai gót chân của Long là 0,4m
Câu 49:
Nhiệt độ ở mặt đất đo được khoảng 300C. Biết rằng cứ lên 1km thì nhiệt độ giảm đi 50.
a) Hãy lập hàm số T theo h, trong đó T tính bằng độ (0) và h tính bằng ki-lô-mét (km)
 Xem đáp án
Xem đáp án
a) Hàm số T theo h là:
T = 30 – 5.hCâu 50:
b) Hãy tính nhiệt độ khi ở độ cao 3km so với mặt đất.
 Xem đáp án
Xem đáp án
b) Thay h = 3 vào công thức T = 30 – 5.h, ta được:
T = 30 – 5.3 = 15
Vậy khi lên độ cao 3km thì nhiệt độ tại đó là 150
Câu 51:
Hiện tại bạn Nam đã để dành được một số tiền là 800 000 đồng. Bạn Nam đang có ý định mua một chiếc xe đạp trị giá 2 000 000 đồng, nên hàng ngày, bạn Nam đều để dành cho mình 20 000 đồng. Gọi m (đồng) là số tiền bạn Nam tiết kiệm được sau t ngày.
a) Thiết lập hàm số của m theo t.
 Xem đáp án
Xem đáp án
a) Hàm số của m theo t là:
m = 20 000.t + 800 000
Câu 52:
b) Hỏi sau bao nhiêu lâu kể từ ngày bắt đầu tiết kiệm thì bạn Nam có thể mua được chiếc xe đạp đó.
 Xem đáp án
Xem đáp án
b) Thay m = 2 000 000 vào công thức m = 20 000.t + 800 000, ta được:
20 000.t + 800 000 = 2 000 000 <=> t = 60
Vậy Nam cần tiết kiệm tiền trong vòng 60 ngày để mua được chiếc xe đạp.
Câu 53:
Với sự phát triển của khoa học kĩ thuật hiện nay, người ta tạo ra nhiều mẫu xe lăn đẹp và tiện dụng cho người khuyết tật. Công ty A đã sản xuất ra những chiếc xe lăn cho người khuyết tật với số vốn ban đầu là 500 triệu đồng. Chi phí để sản xuất ra một chiếc xe lăn là 2 500 000 đồng. Giá bán ra mỗi chiếc là 3 000 000 đồng.

a) Viết hàm số biểu diễn tổng số tiền đã đầu tư đến khi sản xuất ra được x chiếc xe lăn (gồm vốn ban đầu và chi phí sản xuất) và hàm số biểu diễn số tiền thu được khi bán ra chiếc xe lăn.
 Xem đáp án
Xem đáp án
a) Hàm số biểu diễn tổng số tiền y (triệu đồng) đã đầu tư đến khi sản xuất ra được x chiếc xe lăn là:
y = 500 + 2,5.x
Hàm số biểu diễn số tiền thu được y (triệu đồng) khi bán ra x chiếc xe lăn là:
y = 3.x
Câu 54:
 Xem đáp án
Xem đáp án
b) Để số tiền bán được và số vốn đầu tư ban đầu bằng nhau, ta có:
500 + 2,5.x = 3x
Vậy công ty A phải bán 1000 chiếc xe lăn mới thu hồi được vốn ban đầu
Câu 55:
Nhà may A sản xuất một lô áo gồm 200 chiếc áo với giá vốn là 30 000 000 (đồng) và giá bán mỗi chiếc áo sẽ là 300 000 (đồng). Khi đó gọi K (đồng) là số tiền lời (hoặc lỗ) của nhà may thu được khi bán t chiếc áo.
a) Thiết lập hàm số của K theo t.
 Xem đáp án
Xem đáp án
a) Hàm số của K theo t là:
K = 300 000.t – 30 000 000 (với )
Câu 56:
 Xem đáp án
Xem đáp án
b) Thay K = 0 vào công thức K = 300 000.t – 30 000 000, ta được:
0 = 300 000.t – 30 000 000
Vậy cần phải bán ra được 100 chiếc áo mới thu hồi được vốn ban đầu
Câu 57:
 Xem đáp án
Xem đáp án
c) Thay K = 6 000 000 vào công thức K = 300 000.t – 30 000 000, ta được:
6 000 000 = 300 000.t – 30 000 000
Vậy cần phải bán ra được 120 chiếc áo mới lời được 6 000 000 đồngCâu 58:
Một xe ô tô chạy với vận tốc 50km/h từ A đến B. Gọi s (km) là quãng đường xe ô tô đi được trong thời gian t giờ.
a) Hãy lập hàm số của s theo t.
 Xem đáp án
Xem đáp án
a) Hàm số của s theo t là:
s = 50.t
Câu 59:
b) Nếu quãng đường AB dài 150km thì thời gian để xe ô tô đi hết quãng đường AB là bao nhiêu?
 Xem đáp án
Xem đáp án
b)Thay s = 150 vào công thức s = 50.t, ta được:
150 = 50.t <=> t = 3
Vậy thời gian xe ô tô đi hết quãng đường AB là 3 giờCâu 60:
Một người vay ngân hàng 30 000 000 (ba mươi triệu) đồng với lãi suất ngân hàng là 5% một năm và theo thể thức lãi đơn (tiền lãi không gộp vào chung với vốn)
a) Hãy thiết lập hàm số thể hiện mối liên hệ giữa tổng số tiền nợ T (VNĐ) và số nợ (năm).
 Xem đáp án
Xem đáp án
a)Một người vay ngân hàng 30 000 000 VNĐ với lãi suất 5% một năm theo thể thức lãi đơn.
![]() Sau 1 năm người này nợ thêm: 30 000 000.5% = 1 500 000 (VNĐ)
Sau 1 năm người này nợ thêm: 30 000 000.5% = 1 500 000 (VNĐ)
![]() Sau n năm người này nợ thêm: 1 500 000.n (VNĐ)
Sau n năm người này nợ thêm: 1 500 000.n (VNĐ)
Khi đó tổng số tiền người đó nợ sau n năm là: 1 500 000.n + 30 000 000 (VNĐ)
Hàm số thể hiện mối liên hệ giữa tổng số tiền nợ T (VNĐ) và số nợ n (năm) là:
T = 1 500 000.n + 30 000 000
Câu 61:
b) Hãy cho biết sau 4 năm, người đó nợ ngân hàng tất cả bao nhiêu tiền?
 Xem đáp án
Xem đáp án
b)Thay n = 4 vào công thức T = 1 500 000.n + 30 000 000, ta được:
T = 1 500 000.4 + 30 000 000 = 36 000 000
Vậy sau 4 năm người đó nợ ngân hàng là 36 000 000 VNĐ
Câu 62:
Từ ngày 20/12/2014 đến ngày 30/12/2014, Hiệp hội xăng dầu Việt Nam đã thống kê và đi đến kết luận sau: trung bình giá xăng Rol 92 trên thế giới giảm đều mỗi ngày 110 đồng/lít. Biết rằng giá xăng Rol 92 ngày 20/12/2014 là 17 880 đồng/lít.
a) Hỏi giá xăng Rol 92 ở ngày 24/12/2014 là bao nhiêu?
 Xem đáp án
Xem đáp án
a) Giá xăng Rol 92 ở ngày 24/12/2014 là: 17 880 – 110.4 = 17 400 (đồng)
Câu 63:
 Xem đáp án
Xem đáp án
b) Gọi T (đồng) là giá xăng Rol 92 từ ngày 20/12/2014 đến ngày 30/12/2014
Gọi t là số ngày kể từ ngày 20/12/2014 ()
Khi đó, hàm số biểu diễn giá xăng Rol 92 là: T = 17 880 – 110.t (với )
Câu 64:
Trong một xưởng sản xuất đồ gia dụng có tổng cộng 900 thùng hàng và mỗi ngày nhân viên sẽ lấy 30 thùng hàng để đi phân phối cho các đại lí.
a) Gọi T là số thùng hàng còn lại trong kho sau c ngày. Hãy lập hàm số T theo c. Xem đáp án
Xem đáp án
a) Hàm số của T theo c là: T = 900 – 30.c = – 30.c + 900
Câu 65:
 Xem đáp án
Xem đáp án
b) Thay T = 0 vào công thức T = – 30.c + 900, ta được:
– 30.c + 900 = 0
Vậy sau 30 ngày sẽ vận chuyển hết được 900 thùng hàng
Câu 66:
 Xem đáp án
Xem đáp án
c) Tổng số tiền khi bán được 900 thùng hàng là:
900.2 000 000 = 1 800 000 000 (đồng)
Số tiền phải trả cho 30 đợt vận chuyển là:
2 500 000.30 = 75 000 000 (đồng)
Vậy số tiền lời mà xưởng kiếm được là:
1 800 000 000 – 75 000 000 = 1 725 000 000 (đồng)
Câu 67:
Hai bạn Hoa và Hương đi cùng trên một con đường. Lúc đầu bạn Hoa và bạn Hương ở cùng một phía và cách bến xe buýt lần lượt là 200m và 500m cùng đi ngược hướng với trạm xe buýt. Mỗi giờ Hoa đi được 3km và Hương đi được 1km. Gọi d (km) là khoảng cách của Hoa, Hương đối với trạm xe buýt sau khi đi được t giờ.
a) Lập hàm số của d theo t đối với mỗi bạn.
 Xem đáp án
Xem đáp án
a) Hàm số của d theo t đối với bạn Hoa là:
d = 0,2 + 3.t
Hàm số của d theo t đối với bạn Hương là:
d = 0,5 + t
Câu 68:
b) Sau bao lâu thì hai bạn gặp nhau.
 Xem đáp án
Xem đáp án
b) Muốn hai bạn gặp nhau thì khoảng cách của hai bạn đối với trạm xe buýt bằng nhau, nghĩa là:
0,2 + 3.t = 0,5 + t
Vậy sau 0,15 giờ (9 phút) hai bạn sẽ gặp nhau
Câu 69:
Hai người A và B cùng ở một phía và cách thành phố Hồ Chí Minh 50km. Cả hai người cùng nhau đi trên một con đường về phía ngược hướng với thành phố, người A đi với vận tốc là 30km/h và người B đi với vận tốc là 45km/h. Gọi d (km) là khoảng cách từ thành phố Hồ Chí Minh đến hai người A, B sau khi đi được t (giờ).

a) Lập hàm số của d theo t đối với mỗi người.
 Xem đáp án
Xem đáp án
a) Hàm số của d theo t đối với người A là:
d = 50 + 30.t
Hàm số của d theo t đối với người B là:
d = 50 + 45.t
Câu 70:
 Xem đáp án
Xem đáp án
b) Xét:
Vậy sau 2 giờ kể từ lúc xuất phát, khoảng cách giữa hai người là 30km
Câu 71:
Bảng giá cước của một hãng Taxi được cho như sau:

a) Gọi y (đồng) là số tiền khách hàng phải trả sau khi đi x (km). Lập hàm số của y theo x (Giả sử không tính thời gian chờ và phí cầu đường bến bãi)
 Xem đáp án
Xem đáp án
a) Nếu quãng đường khách hàng đi không quá 0,7km, ta có hàm số là:
y = 11 000
Nếu quãng đường khách hàng đi trên 0,7km đến 30km, ta có hàm số là:
y = 11 000 + (x – 0,7).15 800 = 15 800.x – 60
Nếu quãng đường khách hàng đi trên 30km, ta có hàm số là:
y = 11 000 + (30 – 0,7).15 800 + (x – 30).12 500 = 12 500.x + 98940
Câu 72:
 Xem đáp án
Xem đáp án
b) Thay x = 40 vào công thức y = 12 500.x + 98940 (vì 40km > 30km), ta được:
y = 12 500.40 + 98940 = 598940
Vậy hành khách phải trả số tiền là 598940 đồng
Câu 73:
Bạn Luân hiện có số tiền là 32 000 đồng, bạn định sử dụng số tiền này để chơi game, mỗi giờ bạn chơi game tốn 5 000 đồng. Gọi h là số giờ chơi game của bạn Luân và t là số tiền còn lại.
a) Lập hàm số của t theo h
 Xem đáp án
Xem đáp án
a) Hàm số của t theo h là: t = 32 000 – 5 000.h
Câu 74:
 Xem đáp án
Xem đáp án
b) Thay h = 3 vào công thức t = 32 000 – 5 000.h, ta được:
t = 32 000 – 5 000.3 = 17 000
Vậy số tiền bạn Luận còn lại sau khi chơi 3 giờ là 17 000 đồng
Câu 75:
 Xem đáp án
Xem đáp án
c) Xét t > 0 <=> 32 000 – 5 000.h > 0
Vậy Luân chơi tối đa được 6 giờ
Câu 76:
Một người đang dự định đi mua xe máy mà muốn chọn 1 trong hai loại xe sau:
Loại 1: Có giá 27 000 000 (đồng) và trung bình số ki-lô-mét đi được mỗi lít xăng là 58 km/lít xăng.
Loại 2: Có giá 30 000 000 (đồng) và trung bình số ki-lô-mét đi được mỗi lít xăng là 62,5 km/lít xăng.
Biết rằng giá trung bình của 1 lít xăng là 18 000 (đồng). Người ta dự tính mua xe máy để sử dụng khoảng 8 năm. Biết rằng mỗi năm người đó đi được khoảng 7 250 km.

a) Gọi s (đồng) là chi phí từng năm theo thời gian t (năm) của mỗi loại xe (bao gồm tiền mua xe và tiền xăng). Lập hàm số của s theo t.
 Xem đáp án
Xem đáp án
a) Đối với xe loại 1, mỗi năm xe tiêu thụ hết:
7 250 : 58 = 125 (lít)
Suy ra mỗi năm, xe loại 1 tiêu thụ hết:
125.18 000 = 2 250 000 (đồng)
Hàm số của s theo t đối với xe loại 1:
s = 27 000 000 + 2 250 000.t
Đối với xe loại 2, mỗi năm xe tiêu thụ hết:
7 250 : 62,5 = 116 (lít)
Suy ra mỗi năm, xe loại 2 tiêu thụ hết:
116. 18 000 = 2 088 000 (đồng)
Hàm số của s theo t đối với xe loại 2:
s = 30 000 000 + 2 088 000.t
Câu 77:
 Xem đáp án
Xem đáp án
b) Trong thời gian sử dụng 8 năm (t = 8), xe loại 1 tiêu thụ hết:
s = 27 000 000 + 2 250 000.8 = 45 000 000 (đồng)
Trong thời gian sử dụng 8 năm (t = 8), xe loại 2 tiêu thụ hết:
s = 30 000 000 + 2 088 000.8 = 46 704 000 (đồng)
Vậy nên chọn xe loại 1 để tiết kiệm hơn
Câu 78:
c) Thời gian sử dụng là bao lâu thì nên mua xe loại 1?
 Xem đáp án
Xem đáp án
c) Chọn xe loại 2 khi: 27 000 000 + 2 250 000.t 30 000 000 + 2 088 000.t
Vậy thời gian sử dụng là khoảng 19 năm (hoặc nhiều hơn) thì nên chọn xe loại 2
Câu 79:
Một công ty viễn thông A cung cấp dịch vụ truyền hình cáp với mức phí ban đầu là 300 000 đồng và mỗi tháng phải đóng 150 000 đồng. Công ty viễn thông B cũng cung cấp dịch vụ truyền hình cáp nhưng không tính phí ban đầu và mỗi tháng khách hàng sẽ phải đóng 200 000 đồng.
a) Gọi T (đồng) là số tiền khách hàng phải trả cho mỗi công ty viễn thông trong t (tháng) sử dụng dịch vụ truyền hình cáp. Khi đó hãy lập hàm số T theo t đối với mỗi công ty. Xem đáp án
Xem đáp án
a) Hàm số T theo t đối với công ty A là:
T = 150 000.t + 300 000
Hàm số T theo t đối với công ty B là:
T = 200 000.t
Câu 80:
 Xem đáp án
Xem đáp án
b) Thay t = 5 vào công thức T = 150 000.t + 300 000, ta được:
T = 150 000.5 + 300 000 = 1 050 000 (đồng)
Vậy đối với công ty A, sau khi sử dụng dịch vụ truyền hình cáp trong 5 tháng thì số tiền phải trả là đồng
Thay t = 5 vào công thức T = 200 000.t, ta được:
T = 200 000.5 = 1 000 000 (đồng)
Vậy đối với công ty B, sau khi sử dụng dịch vụ truyền hình cáp trong 5 tháng thì số tiền phải trả là đồng
Câu 81:
 Xem đáp án
Xem đáp án
c) Để dịch vụ truyền hình cáp của công ty A lợi hơn dịch vụ truyền hình cáp của công ty B thì:
150 000.t + 300 000 < 200 000.t <=> 300 000 < 50 000.t <=> t > 6
Vậy nếu sử dụng từ 7 tháng trở lên thì sử dụng dịch vụ truyền hình cáp bên công ty A sẽ có lợi hơn.
Câu 82:
Có hai hãng điện thoại cố định tính phí gọi cho các thuê bao như sau:
|
Hãng |
Thuê bao (ngàn đồng) |
Gọi nội hạt (ngàn đồng/30 phút) |
|
Hãng A |
10 |
6 |
|
Hãng B |
15 |
5 |
Gọi y là giá tiền mà khách hàng phải trả sau x lần 30 phút
Biết cước phí hàng tháng bằng tổng tiền thuê bao và cước phí gọi nội hạt.
a) Hãy biểu diễn y theo x của từng hãng.
 Xem đáp án
Xem đáp án
Tiền cước phí phải trả cho hãng A mỗi tháng là: y = 10 + 6x
Tiền cước phí phải trả cho hãng B mỗi tháng là: y = 15 + 5x
Câu 83:
 Xem đáp án
Xem đáp án
b) Ta có: 6 giờ = 360 phút = 12.30 phút ![]() x = 12
x = 12
Khi x = 12, ta có:
+ y = 10 + 6x = 10 + 6.12 = 82
+ y = 15 + 5x = 15 + 5.12 = 75
Vậy khách hàng nên sử dụng hãng B sẽ rẻ hơn (vì 75 ngàn đồng < 82 ngàn đồng)
Câu 84:
 Xem đáp án
Xem đáp án
c) Xét 10 + 6x 15 + 5x <=> x 5
Vậy khách hàng gọi bình quân dưới 2,5 giờ (5 lần 30 phút) thì có lợi khi sử dụng hãng A.
Câu 85:
Bảng giá cước gọi quốc tế của công ty viễn thông A được cho bởi bảng sau:
|
Thời gian gọi (phút) |
Giá cước điện thoại (đồng/phút) |
|
Không quá 8 phút |
6 500 |
|
Từ phút thứ 9 đến phút thứ 15 |
6 000 |
|
Từ phút thứ 16 đến phút thứ 25 |
5 500 |
|
Từ phút thứ 26 trở đi |
5 000 |
a) Gọi T (đồng) là số tiền khách hàng phải trả khi gọi quốc tế trong t phút. Lập hàm số của T theo t.
 Xem đáp án
Xem đáp án
a) Nếu khách hàng gọi quốc tế không quá 8 phút, ta có hàm số là:
T = 6500.t (với t 8)
Nếu khách hàng gọi quốc tế trên 8 phút và không quá 15 phút, ta có hàm số là:
T = 8.6500 + (t – 8).6000 = 6000.t + 4000 (với 8 < t 15)
Nếu khách hàng gọi quốc tế trên 15 phút và không quá 25 phút, ta có hàm số là:
T = 8.6500 + (15 – 8).6000 + (t – 15).5500 = 5500.t + 11500 (với 15 < t 25)
Nếu khách hàng gọi quốc tế trên 25 phút, ta có hàm số là:
T = 8.6500 + (15 – 8).6000 + (25 – 15).5500 + (t – 25).5000 = 5000t + 24000 (với t > 25)
Câu 86:
b) Nếu ông A gọi quốc tế 12 phút. Hãy tính số tiền mà ông A phải trả?
 Xem đáp án
Xem đáp án
b)Ta thấy 12 phút thuộc khoảng từ phút thứ 9 đến phút thứ 15
![]() Thay t = 12 vào công thức T = 6000.t + 4000, ta được:
Thay t = 12 vào công thức T = 6000.t + 4000, ta được:
T = 6000.12 + 4000 = 76 000
Vậy ông A phải trả số tiền là 76 000 đồng
Câu 87:
 Xem đáp án
Xem đáp án
c) Thay t = 25 vào công thức T = 5000t + 24000, ta được:
T = 5000.25 + 24000 = 149 000
Ta thấy rằng 174 000 > 149 000 nên ông B phải gọi quốc tế trên 25 phút
Số phút ông B gọi là: (phút)
Câu 88:
Một cửa hàng sách cũ có một chính sách như sau: nếu khách hàng đăng kí làm hội viên của cửa hàng sách thì mỗi năm phải đóng 50 000 đồng chi phí và chỉ phải mướn sách với giá 5 000 đồng/cuốn sách, còn nếu khách hàng không phải hội viên thì sẽ mướn sách với giá 10 000 đồng/cuốn sách. Gọi s (đồng) là tổng số tiền mỗi khách hàng phải trả trong mỗi năm và t là số cuốn sách mà khách hàng mướn.
a) Lập hàm số của s theo t đối với khách hàng là hội viên và với khách hàng không phải là hội viên.
 Xem đáp án
Xem đáp án
a) Đối với khách hàng là hội viên, ta có hàm số:
s = 5 000.t + 50 000
Đối với khách hàng không là hội viên, ta có hàm số:
s = 10 000.t
Câu 89:
 Xem đáp án
Xem đáp án
b) Trung là hội viên nên số tiền Trung bỏ ra cho mỗi năm sẽ được tính theo công thức:
s = 5 000.t + 50 000
Thay s = 90 000 vào công thức s = 5 000.t + 50 000, ta được:
90 000 = 5 000.t + 50 000
Vậy năm ngoái Trung trả tổng cộng 90 000 đồng nên số sách Trung đã mượn là 8 cuốn
Thay t = 8 vào công thức s = 10 000.t, ta được:
s = 10 000.8 = 80 000
Vậy nếu không phải là hội viên thì số tiền Trung phải trả cho năm ngoái là 80 000 đồng
Câu 90:
c) Một hội viên cần thuê tối thiểu bao nhiêu cuốn sách để có thể bù được phí hội viên?
 Xem đáp án
Xem đáp án
Khi là hội viên thì với mỗi cuốn sách mướn khách hàng sẽ tiết kiệm được 5 000 đồng so với khách không phải là hội viên
Để bù được phí hội viên thì số tiền tiết kiệm được khi mướn t cuốn sách phải lớn hơn hoặc bằng phí hội viên: 5000.t
Vậy cần phải mướn ít nhất 10 cuốn sách để có thể bù được phí hội viên
Câu 91:
Một xí nghiệp may cứ mỗi tháng thì phải trả tiền lương cho công nhân viên, tiền vật liệu, tiền điện, tiền thuế,… tổng cộng là 410 000 000 (VNĐ). Mỗi chiếc áo được bán với giá là 350 000 (VNĐ). Gọi số tiền lời (hoặc lỗ) mà xí nghiệp thu được sau mỗi tháng là L (VNĐ) và mỗi tháng xí nghiệp sản xuất được A chiếc áo.
a) Lập hàm số của L theo A.
 Xem đáp án
Xem đáp án
a) Hàm số của L theo A là:
L = 350 000.A – 410 000 000
Câu 92:
b) Nếu trong một tháng, công ty bán được 1 000 chiếc áo thì công ty lời hay lỗ bao nhiêu?
 Xem đáp án
Xem đáp án
b) Thay A = 1000 vào công thức L = 350 000.A – 410 000 000, ta được:
L = 350 000.1000 – 410 000 000 = ![]() 60 000 000
60 000 000
Vậy xí nghiệp sẽ lỗ 60 000 000 đồng
Câu 93:
c) Mỗi tháng phải sản xuất ít nhất bao nhiêu chiếc áo để xí nghiệp không bị lỗ?
 Xem đáp án
Xem đáp án
c) Xét
Vậy xí nghiệp cần phải bán ít nhất 1172 chiếc áo thì xí nghiệp không bị lỗCâu 94:
 Xem đáp án
Xem đáp án
d) Trung bình mỗi tháng, xí nghiệp cần phải lời:
(VNĐ)
Thay L = 115 000 000 vào công thức L = 350 000.A – 410 000 000, ta được:
115 000 000 = 350 000.A – 410 000 000
Vậy trung bình mỗi tháng, xí nghiệp cần bán được 1500 chiếc áo
Câu 95:
Hãng taxi thứ nhất có giá như sau: mở cửa là 10 ngàn đồng, sau đó mỗi km giá 12 ngàn đồng. Hãng taxi thứ hai có giá như sau: mỗi km tính giá 14 ngàn đồng.
a) Viết công thức tính y (số tiền khách phải trả) theo x (số km xe chở khách) của hai hãng xe taxi. Vẽ đồ thị của hai hàm số này trên cùng một hệ trục tọa độ. Xác định tọa độ giao điểm.
b) Dựa trên đồ thị ở câu a, theo em, chọn đi xe taxi của hãng thứ nhất sẽ có lợi hơn xe taxi của hãng thứ hai khi nào?
 Xem đáp án
Xem đáp án
a) Công thức tính số tiền phải trả của hãng xe taxi thứ nhất: y = 12x + 10
Công thức tính số tiền phải trả của hãng xe taxi thứ hai: y = 14x
Đồ thị:
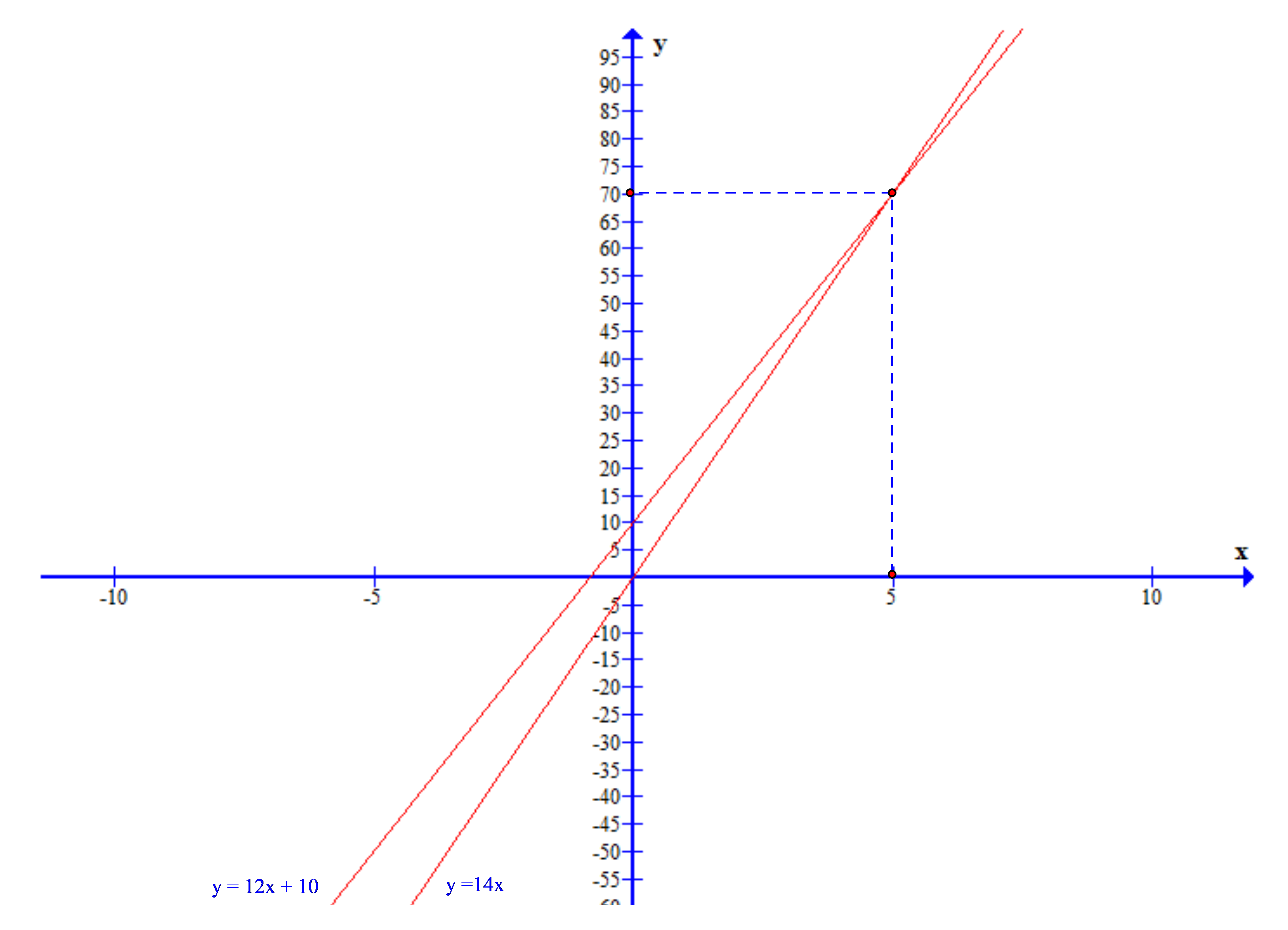
Tọa độ giao điểm của hai đồ thị là (5; 70)
b) Nhìn trên đồ thị, ta thấy x < 5 thì đồ thị hàm số thứ nhất thấp hơn đồ thị hàm số thứ hai. Điều đó nghĩa là khi đi đoạn đường ngắn hơn 5km thì giá thành của hãng taxi thứ nhất rẻ hơn, hãy chọn hãng xe taxi thứ nhất.
Câu 96:
Một người muốn mua một trong hai loại tủ lạnh sau: Tủ A giá 3 triệu đồng và tiêu thụ 500kwh điện mỗi năm, tủ B giá 4 triệu đồng và tiêu thụ 400kwh điện mỗi năm. Giá mỗi kwh điện là 2 000 đồng và người đó muốn mua về để sử dụng trong 4 năm.

 Xem đáp án
Xem đáp án
a) Giá 500kwh là: 500.2000 = 1 000 000 đồng = 1 triệu đồng
Giá 400kwh là: 400.2000 = 800 000 đồng = 0,8 triệu đồng
Biểu thức tính tổng số tiền chi phí cho tủ lạnh loại A là: y = x + 3
Biểu thức tính tổng số tiền chi phí cho tủ lạnh loại B là: y = 0,8x + 4
Trong đó, x là chi phí tiền điện trong một năm (đơn vị: triệu đồng), y là tổng chi phí cho mỗi loại tủ lạnh theo năm, gồm tiền mua tủ lạnh và tiền điện (đơn vị: triệu đồng)
Câu 97:
 Xem đáp án
Xem đáp án
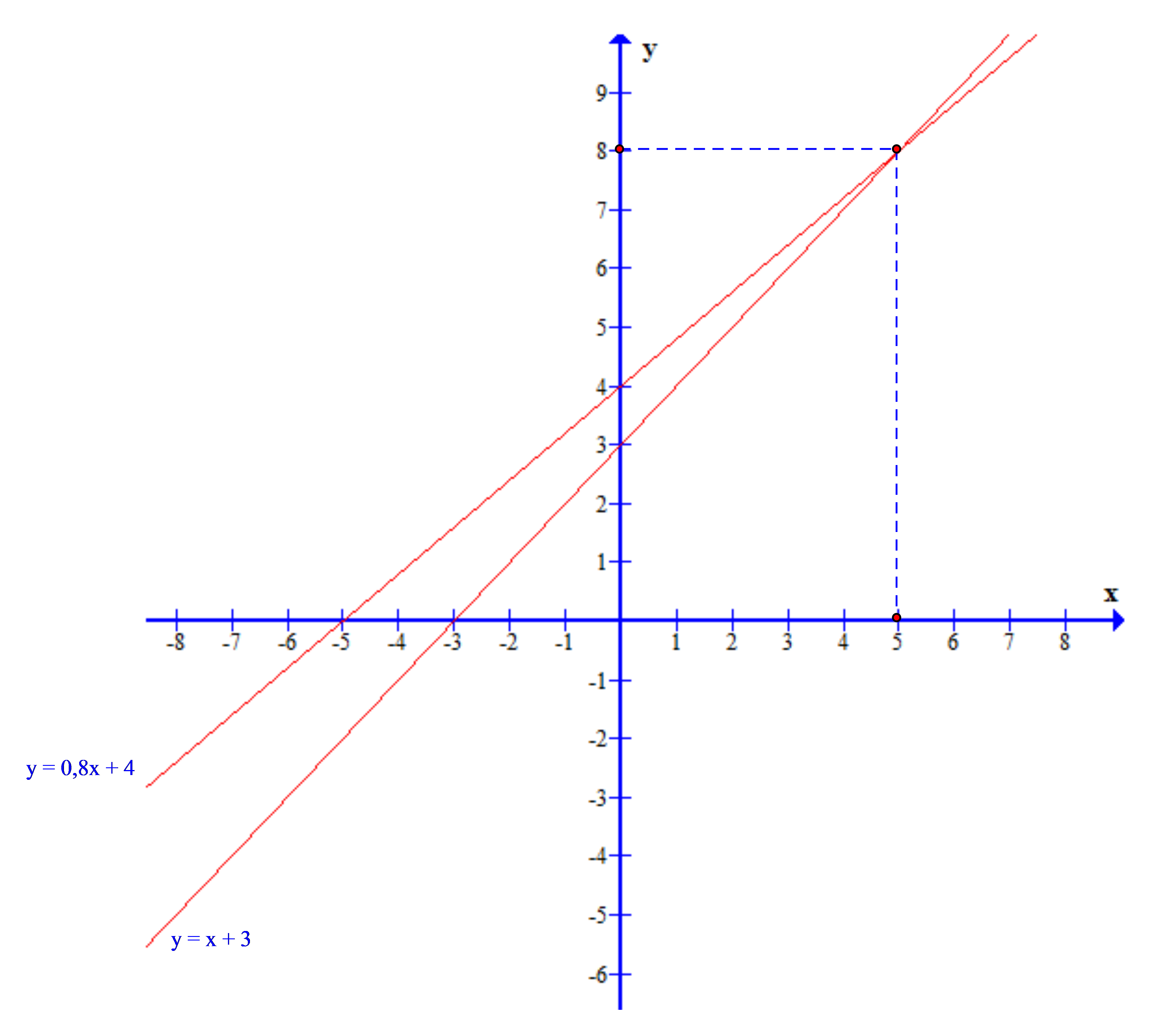
Nếu thời gian sử dụng < 5 năm thì: số chi phí phải trả cho máy thứ nhất thấp hơn.
Nếu thời gian sử dụng = 5 năm thì: số chi phí phải trả cho 2 máy là bằng nhau.
Nếu thời gian sử dụng > 5 năm thì: số chi phí phải trả cho máy thứ nhất cao hơn.
Câu 98:
Một trường có hơn 1500 học sinh muốn tổ chức đêm ca nhạc cuối năm. Chi phí cho trang trí và âm thanh là 4
triệu đồng, cho bảo vệ phục vụ và điều hành chung là 1,5 triệu đồng. Tiền in vé là 1000 đồng cho 20 vé. Dự tính
giá vé là 10 nghìn đồng. Hỏi phải bán được ít nhất bao nhiêu vé mới có lãi hơn hơn 5000000 đồng để mua quà
cho các chiến sĩ đang canh gác vùng hải đảo xa xôi?
 Xem đáp án
Xem đáp án
Gọi x là số vé cần bán, .
Tiền lãi của một vé là: (đồng).
Tiền lãi sau khi bán được x vé là: (đồng).
Để lãi được ít nhất 5 triệu đồng ta có bất phương trình sau:
Do đó, số vé cần bán ít nhất là 1056 (vé) mới có lãi hơn đồng.
Câu 99:
“Vàng 24K còn gọi là vàng ròng (hay vàng nguyên chất) là một kim loại có ánh kim đậm nhất nhưng khá mềm.
Trong ngành công nghệ chế tạo trang sức, người ta ít dùng vàng 24K mà thay thế bằng vàng 14K là hợp kim của
vàng và đồng để dễ đánh bóng và tạo ra nhiều kiểu dáng đa dạng”. Một món trang sức được làm từ vàng 14K có
thể tích và nặng 151,8g. Hãy tính thể tích vàng nguyên chất và đồng được dùng để làm ra món trang sức
biết khối lượng riêng của vàng nguyên chất là khối lượng riêng của đồng là và công thức liên hệ
giữa khối lượng và thể tích là .
 Xem đáp án
Xem đáp án
Gọi lần lượt là thể tích của vàng nguyên chất và đồng có trong món trang sức.
Theo đề ta có: x+y=10 (1)
Khối lượng vàng nguyên chất trong món trang sức là: 19,3x(g)
Khối lượng đồng trong món trang sức là:9,2y(g)
Do đó: 19,3x+9y=151,8 (2)
Từ (1) và (2), ta có hệ phương trình:
Vậy thể tích của vàng nguyên chất trong món trang sức là
Thể tích của đồng trong món trang sức là
Câu 100:
Trái bóng Telstar xuất hiện lần đầu tiên ở World Cup 1970 ở Mexico do Adidas sản xuất có đường kính 22,3cm. Trái bóng được may từ 32 múi da đen và trắng. Các múi da màu đen hình ngũ giác đều, các múi da màu trắng hình lục giác đều. Trên bề mặt trái bóng, mỗi múi da màu đen có diện tích 37cm2, Mỗi múi da màu trắng có diện tích 55,9cm2. Hãy tính trên trái bóng có bao nhiêu múi da màu đen và màu trắng?
 Xem đáp án
Xem đáp án
Trước tiên ta tính diện tích bề mặt trái bóng: với . Vậy
Gọi lần lượt là số múi da đen và trắng trên trái bóng Telstlar. Khi đó vì 32 múi da đen và trắng phủ kín bề mặt trái bóng nên ta có biểu thức :
Lại có số múi da đen và trắng tổng cộng là 32 nên ta có : x+y=32
Vậy ta có hệ pt sau:
Vậy có tất cả 12 múi da đen và 20 múi da trắng.
Câu 101:
Cho biết rừng nhiệt đới trên trái đất được xác định bởi hàm số bậc nhất y = ax + b, trong đó y là đại lượng biểu thị diễn tích rừng nhiệt đới, tính bằng đơn vị ha, x là đại lượng biểu thị số năm tính từ năm 2000. Năm 2002 diện tích rừng nhiệt đới trên trái đất là 709,1 triệu ha. 8 năm sau, nhiệt tích rừng nhiệt đới trên trái đất là672,3 triệu ha.
a) Hãy xác định a và b
 Xem đáp án
Xem đáp án
Ta có: y = ax + b
Năm 2002 diện tích rừng nhiệt đới trên trái đất là 709,1 triệu ha nên: 709,1 = a.(2002 – 2000) + b
8 năm sau, nhiệt tích rừng nhiệt đới trên trái đất là672,3 triệu ha nên : 672,3 = a.( 8 + 2) + b
Từ (1) và (2), ta có :
Vậy : y = - 4,6x + 718,3
Câu 102:
b) Hãy tính diện tích rừng nhiệt đới trên trái đất vào các năm 2000; 2020
 Xem đáp án
Xem đáp án
b)
Thay x = 2000 vào
Thay x = 2020 vào :
Vậy: Diện tích rừng nhiệt đới trên trái đất vào các năm 2000 là 718,3 triệu ha.
Diện tích rừng nhiệt đới trên trái đất vào các năm 2020 là 626,3 triệu ha.
Câu 103:
 Xem đáp án
Xem đáp án
Gọi x,y (học sinh) là số học sinh nam và nữ cần tìm.
Điều kiện: .
Vì lớp học có 40 học sinh nên có phương trình x+y=40 (1).
Vì cô giáo đưa cả lớp 260 000 đồng để mỗi bạn nam mua một ly Coca giá 5 000 đồng/ly, mỗi bạn nữ mua một bánh phô mai giá 8 000 đồng/cái và được căn tin thối lại 3 000 đồng nên có phương trình: .
Từ (1) và (2) ta có hệ phương trình: (thỏa điều kiện).
Vậy số học nam của lớp là học sinh.
Số học sinh nữ của lớp là học sinh.
Câu 104:
Có 2 thỏi thép vụn , 1 thỏi chứa 10% Niken và 1 thỏi chứa 35% Niken. Hỏi cần cần bao nhiêu tấn thép vụn mỗi loại kể trên để luyện được 140 tấn thép chứa 30% Niken.
 Xem đáp án
Xem đáp án
Gọi x là khối lượng thỏi chứa 10% Niken
y là khối lượng thỏi chứa 35% Niken
Ta có hệ phương trình:
Vậy để luyện được 140 tấn thép chứa 30% Niken thì cần 40 tấn thép vụn chứa 10% Niken và 100 tấn thép vụn chứa 35% Niken
Câu 105:
 Xem đáp án
Xem đáp án
Gọi x,y lần lượt là khối lượng sắt vụn mỗi loại , tấn
Theo đề bài ta có hệ phương trình :
giải ra ta có x=28 và y=112 (thỏa điều kiện)
Câu 106:
Bác A vay 2 000 000 đồng của ngân hàng để làm kinh tế gia đình trong thời hạn một năm. Lẽ ra cuối năm bác phải trả cả vốn lẫn lãi. Song bác được ngân hàng cho kéo dài thời hạn thêm một năm nữa. Số tiền lãi của năm trước được gộp vào với tiền vốn để tính lãi năm sau, và lãi suất vẫn như cũ. Hết hai năm bác phải trả cho ngân hàng tất cả là 2 420 000 đồng. Hỏi lãi suất cho vay của ngân hàng là bao nhiêu phần trăm?
 Xem đáp án
Xem đáp án
Gọi r% là lãi suất ngân hàng một năm (r > 0)
Theo công thức lãi kép
Số tiền bác A phải trả cho ngân hàng sau 2 năm là:
2 000 000. (đồng)
Theo đề bài, ta có phương trình:
2 000 000.(1 + r%)2 = 2 420 000
<=> r = 10 (nhận)
Vậy lãi suất cho vay của ngân hàng là 10%/năm.
Câu 107:
 Xem đáp án
Xem đáp án
Gọi r% là lãi suất trong một năm đầu của ngân hàng (r > 0)
Tiền lãi năm thứ nhất là:
20 000 000. 200 000.r (đồng)
Tổng số tiền cả vốn lẫn lãi sau 1 năm là:
20 000 000 + 200 000.r (đồng)
Lãi suất của ngân hàng trong năm thứ hai là:
r% – 30%.r% = 0,7r%
Tiền lãi năm thứ hai là:
(20 000 000 + 200 000.r). = 1400r2 + 140000r (đồng)
Tổng số tiền cả vốn lẫn lãi sau 2 năm là:
20 000 000 + 200 000.r + 1400r2 + 140000r = 1400r2 + 340000r + 20 000 000 (đồng)
Theo đề bài, ta có phương trình:
1400r2 + 340000r + 20 000 000 = 23 540 000
<=> 1400r2 + 340000r – 3 540 000 = 0
Vì r > 0 nên r = 10 (nhận); r (loại)
Vậy lãi suất cho vay của ngân hàng là 10% trong một năm đầu.Câu 108:
 Xem đáp án
Xem đáp án
Bạn Nam mua quà 78000 và được thối lại 1000 tức là bạn mang theo 79000 đồng.
Gọi a,b lần lượt là số tờ tiền loại 2000 và 5000 đồng.
Tổng giá trị tiền bạn Nam mang theo là 79000:
Số tờ tiền bạn Nam mang theo là 20: a+b=20
Ta có hệ phương trình:. Vậy Nam có 7 tờ 2000, 13 tờ 5000.
Câu 109:
Một hình chữ nhật nếu tăng dài thêm 10m và tăng rộng thêm 5m thì diện tích tăng thêm 500m2. Nếu giảm dài 15m và giảm rộng 9m thì diện tích giảm 600m2. Tính chiều dài, chiều rộng ban đầu.
 Xem đáp án
Xem đáp án
Gọi a,b lần lượt là chiều dài, chiều rộng hình chữ nhật ban đầu.
Diện tích ban đầu:
Diện tích sau khi tăng chiều dài 10m, tăng chiều rộng 5m:
Diện tích sau khi giảm chiều dài 15m, giảm chiều rộng 9m:
Ta có hệ phương trình:
Vậy chiều dài, chiều rộng hình chữ nhật lần lượt là 40m;25m.Câu 110:
Một mảnh vườn hình chữ nhật được chia thành nhiều luống để trồng cải, biết mỗi luống trồng số cây như nhau. Nếu tăng 8 luống và mỗi luống trồng ít hơn dự định 3 cây thì tổng số cây trồng được ít hơn dự định 54 cây. Nếu giảm 4 luống và mỗi luống trồng thêm 2 cây thì tổng số cây trồng nhiều hơn dự định là 32 cây. Hỏi số luống và số cây dự định.
 Xem đáp án
Xem đáp án
Gọi a là số luống ban đầu, b là số cây trồng trên 1 luống ban đầu
T.h.1: tăng 8 luống và mỗi luống trồng ít hơn dự định 3 cây thì tổng số cây trồng được ít hơn dự định 54 cây:
T.h.2: giảm 4 luống và mỗi luống trồng thêm 2 cây thì tổng số cây trồng nhiều hơn dự định là 32 cây:
Ta có hệ phương trình:
Vậy theo dự định có 50 luống, trồng 15 cây mỗi luống và tổng cộng 750 cây.
Câu 111:
 Xem đáp án
Xem đáp án
Gọi vận tốc của ôtô và xe máy lần lượt là x và y.
Biết vận tốc ôtô hơn xe máy 15 km/h (1)
Lúc 7 giờ sáng, xe máy đi từ A tới B và gặp ôtô lúc 11 giờ → xe máy đi được 4 giờ. Lúc 9 giờ ôtô đi từ B về A và gặp xe máy lúc 11 giờ → ôtô đi được 2 giờ.
Dựa vào công thức s = v.t → (2)
Từ (1) và (2) suy ra
Câu 112:
 Xem đáp án
Xem đáp án
y (kg) là số kg xoài của thùng trái cây.
Điều kiện: x, y N*; x, y <16
Do thùng trái cây nặng 16kg gồm táo và xoài nên: x + y = 16 (1)
Số tiền mua táo là: x. 50.000 (đồng)
Số tiền mua xoài là: y. 70.000 (đồng)
Tổng số tiền của thùng trái cây là 1.000.000đồng nên: x. 50.000 + y. 70.000 = 1.000.000 (2)
Từ (1) và (2) ta có hệ phương trình:
Vậy thùng trái cây có 6kg táo và 10 kg xoài
Câu 113:
Một xe tải có chiều rộng là 2,4 m chiều cao là 2,5 m muốn đi qua một cái cổng hình Parabol. Biết khoảng cách giữa hai chân cổng là 4m và khoảng cách từ đỉnh cổng tới mỗi chân cổng là m( Bỏ qua độ dày của cổng).
1) Trong mặt phẳng tọa độ Oxy gọi Parabo với a<0 là hình biểu diễn cổng mà xe tải muốn đi qua. Chứng minh a=-1.
2) Hỏi xe tải có đi qua cổng được không? Tại sao?
 Xem đáp án
Xem đáp án

2) Để đáp ứng chiều cao trước hết xe tải phải đi vào chính giữa cổng.
Xét đường thẳng (ứng với chiều cao của xe). Đường thẳng này cắt Parabol tại 2 điểm có tọa độ thỏa mãn hệ:
suy ra tọa độ hai giao điểm là . Vậy xe tải có thể đi qua cổng.
Câu 114:
Thả một vật nặng từ trên cao xuống, chuyển động của vật được gọi là vật rơi tự do. Biết rằng quãng đường đi được của vật được cho bởi công thức . Với s là quãng đường rơi của vật tính bằng m; t là thời gian rơi tính bằng giây.
a) Nếu thả vật từ độ cao 122,5m thì sau bao lâu vật chạm đất.
 Xem đáp án
Xem đáp án
Theo đề bài ta có: s = 122,5 m.
Quãng đường vật đi được là:
Vì t là thời gian rơi nên t > 0, ta nhận t=5
Vậy sau 5 giây thì vật chạm đất nếu thả từ độ cao 122,5 m
Câu 115:
 Xem đáp án
Xem đáp án
Câu 116:
 Xem đáp án
Xem đáp án
Theo đề ta có:
Nồng độ muối trong dung dịch I là:
Nồng độ muối trong dung dịch II là:
Vì nồng độ muối trong dung dịch I nhiều hơn nồng độ muối trong dung dịch II nên:
Từ (1) và (2), ta có hệ phương trình:
Ta có:
Với
Vậy khối lượng dung dịch I là 100kg và khối lượng dung dịch II là 120kg .
Câu 117:
 Xem đáp án
Xem đáp án
Lợi nhuận của công ty khi bán đĩa y với giá x (nghìn đồng) mỗi đĩa là: (nghìn đồng)
Ta có:
Để công ty thu lợi nhuận cao nhất thì có giá trị lớn nhất
Mà lớn nhất bằng 1600 khi dấu "=" của bất đẳng thức xảy ra,
khi đó
Vậy công ty cần bán mỗi đĩa giá 80 (nghìn đồng) để thu được lợi nhuận cao nhất.
Câu 118:
 Xem đáp án
Xem đáp án
Sau 6 tháng đầu tiên, giá chiếc áo còn: (đồng)
Sau 6 tháng nữa, giá chiếc áo còn:
Theo đề ta có:
Vậy mỗi lần khuyến mãi,chiếc áo được giảm 25%.
Câu 119:
a) Tính vận tốc ôtô khi t bằng 5 phút.
 Xem đáp án
Xem đáp án
Vận tốc khi t = 5 phút là:
Câu 120:
 Xem đáp án
Xem đáp án
Ta có:
Dấu “ = ” xảy ra khi .
Vậy vận tốc nhỏ nhất khi t = 5.
Câu 121:
 Xem đáp án
Xem đáp án
S = (25 + x)(40 + x) = x2 + 65x + 1000 => S không phải là hàm số bậc nhất của x vì S không có dạng y = ax + b
P = 2(25 + x + 40 + x) = 4x + 130 => P là hàm số bậc nhất của x vì P có dạng y = ax + b trong đó a = 4 ; b = 130
P = 144 => 144 = 4x + 130 Þ x = 3,5
Câu 122:
 Xem đáp án
Xem đáp án
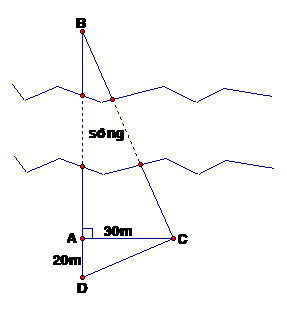
a) AC2 = AB.AD (HTL trong tam giác vuông)
=> 302 = AB.20 => AB = 45(m)
DABC vuông, có:
Câu 123:
Có 150g dung dịch chứa 40g muối. Ta phải pha thêm bao nhiêu nước nữa để dung dịch có tỉ lệ 20% muối.
 Xem đáp án
Xem đáp án
Khối lượng dung dịch có tỉ lệ 20% muối :
Khối lượng nước cần pha thêm : 200 – 150 = 50(g)
Câu 124:
 Xem đáp án
Xem đáp án
T = 500a + 45000
a = 50 => T = 500 . 50 + 45000 = 70 000 (đơn vị tiền tệ)
a = 62 => T = 500 . 62 + 45000 = 76 000 (đơn vị tiền tệ)
a = 96 => T = 500 . 96 + 45000 = 93 000 (đơn vị tiền tệ)
Câu 125:
Bạn An có tầm mắt cao 1,5m đứng gần một tòa nhà cao thì thấy nóc của tòa nhà với góc nâng 300. An đi về phía tòa nhà 20m thì nhìn thấy nóc tòa nhà với góc nâng bằng 650. Tính chiều cao của tòa nhà. (Kết quả làm tròn với chữ số thập phân thứ nhất).
 Xem đáp án
Xem đáp án
Theo đề bài ta có hình vẽ sau :
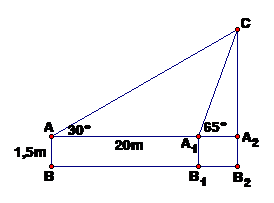
Chiều cao của tòa nhà :
CB2 = CA2 + A2B2
CB2 = 15,8 + 1,5 = 17,3(m)
Câu 126:
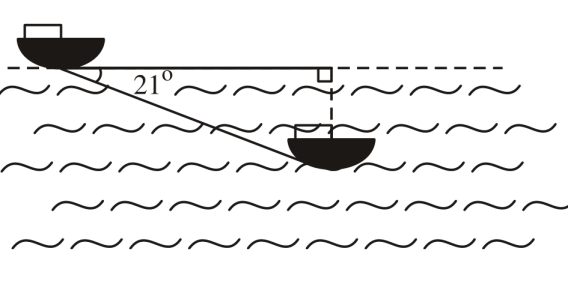
Trong buổi tập luyện, một tàu ngầm đang ở trên mặt biển bắt đầu lặn xuống và di chuyển theo đường thẳng tạo với mặt nước biến một góc 210 (xem hình bên).
a) Khi tàu chuyển động theo hướng đó và đi được 200m thì tàu sẽ ở độ sâu bao nhiêu so với mặt nước biển? (làm tròn đến đơn vị mét)
b) Giả sử tốc độ trung bình của tàu là 9 km/h, thì sau bao lâu (tính từ lúc bắt đầu lặn) tàu ở độ sâu 200m (cách mặt nước biển 200m)? (làm tròn đến phút)
 Xem đáp án
Xem đáp án
Theo đề bài ta có hình vẽ sau:
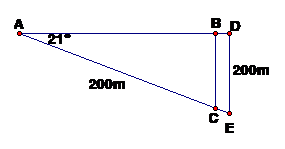
a) Xét DABC vuông, có:
BC » 72 (m)
Vậy: tàu ở độ sâu so với mặt nước biển là 72m
b) Xét DABC vuông, có:
» 558(m)
Quãng đường tàu đi được là 558m
Thời gian tàu lặn xuống ở độ sâu 200m:
(phút)
Câu 127:
Một công nhân làm việc với mức lương cơ bản là 200 000 đồng cho 8 giờ làm việc trong một ngày. Nếu trong một tháng người đó làm 26 ngày và tăng ca thêm 3 giờ/ngày trong 10 ngày thì người đó nhận được bao nhiêu tiền lương? Biết rằng tiền lương tăng ca bằng 150% tiền lương cơ bản.
 Xem đáp án
Xem đáp án
Tiền lương căn bản trong 1 giờ: (đồng)
Tiền lương tăng ca trong 1 ngày: (đồng)
Tiền lương nhận được trong 1 tháng:
(200 000 . 26) + 112 500 . 10 = 6 325 000(đồng)
Câu 128:
Các nhà sản xuất cho biết: khi để một cái tivi ở trạng thái “chờ” (chỉ tắt tivi bằng điều khiển không dây) thì trong một giờ tivi vẫn tiêu thụ một lượng điện năng là 1Wh. Giả thiết rằng trung bình mỗi hộ gia đình ở thành phố Hồ Chí Minh có một tivi và xem 6 giờ mỗi ngày. Em hãy tính, nếu tất cả các hộ gia đình ở thành phố đều tắt tivi ở trạng thái “chờ” thì mỗi tháng (tính là 30 ngày) cả thành phố đã không tiết kiệm bao nhiêu tiền? (biết rằng giá điện trung bình là 1800 đồng/kWh và thành phố có khoảng 1,7 triệu hộ gia đình).
 Xem đáp án
Xem đáp án
Số giờ tivi ở trạng thái “chờ”: 24 – 6 = 18 (giờ)
Số tiền cả thành phố đã không tiết kiệm được:
18 . (1.10–3) . (1,7.106) . 1800 . 30 = 1 652 400 000 (đồng)
Câu 129:
 Xem đáp án
Xem đáp án
Gọi x(m) là chiều rộng hình chữ nhật (x > 0)
Chiều dài hình chữ nhật là 2x (m)
Theo đề bài ta có: x . 2x = 338 <=> x = 13 (nhận)
Chu vi miếng đất : (x + 2x).2 = 6x = 6 . 13 = 78(m)
Câu 130:
Từ một tòa nhà cao tầng, một người (ở vị trí A) có tầm mắt cách mặt đất 30m nhìn xuống vị trí C dưới một góc hạ là 600. Tính khoảng cách từ chân tòa nhà (vị trí B) đến C. (Làm tròn đến chữ số thập phân thứ 2)
 Xem đáp án
Xem đáp án
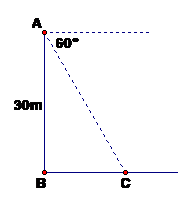
(so le trong)
Câu 131:
Một miếng đất hình vuông có diện tích bằng diện tích của một hình chữ nhật, biết hình chữ nhật đó có độ dài bằng 48 m, chiều rộng bằng 8 m. Hỏi cạnh miếng đất hình vuông đó có độ dài bằng bao nhiêu? (làm tròn đến chữ số thập phân thứ ba).
 Xem đáp án
Xem đáp án
Diện tích hình vuông bằng diện tích hình chữ nhật: 48 . 8 = 384 (m2)
Cạnh miếng đất hình vuông:
Câu 132:
Các nhà khoa học về thống kê đã thiết lập được hàm số sau: A(t) = 0,08t + 19,7 trong đó A(t) là độ tuổi trung bình các phụ nữ kết hôn lần đầu của thế giới; t là năm kết hôn, với gốc thời gian là 1950 nghĩa là năm 1950 thì t = 0, năm 1951 thì t = 1, năm 1952 thì t = 2, …
Hãy tính độ tuổi trung bình các phụ nữ kết hôn lần đầu lần lượt vào các năm 1980, 2005, 2017, 2020 (làm tròn đến chữ số thập phân thứ hai).
 Xem đáp án
Xem đáp án
A(t) = 0,08t + 19,7
Năm 1980 2005 2017 2020
t 30 55 67 70
A(t) 22,10 24,10 25,06 25,30
Câu 133:
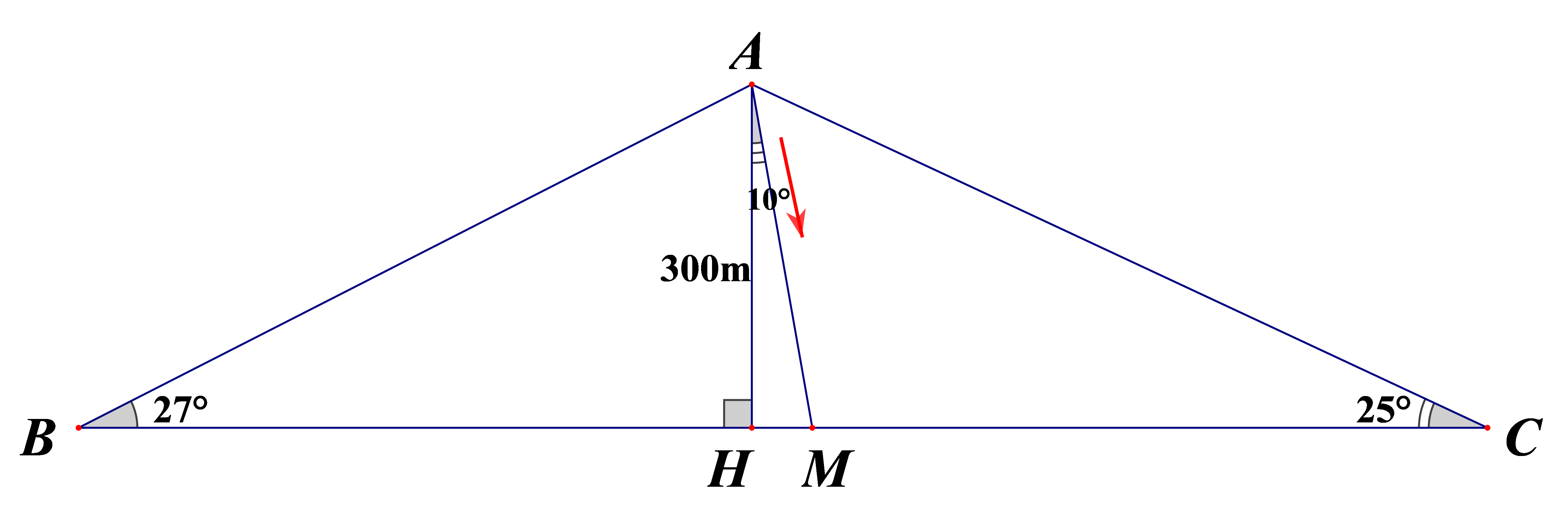
Hai người từ hai vị trí quan sát B và C nhìn thấy một chiếc máy bay trực thăng (ở vị trí A) lần lượt dưới góc 270 và 250 so với phương nằm ngang (trên hình 1). Biết máy bay đang cách mặt đất theo phương thẳng đứng 300 m.
a) Tính khoảng cách BC giữa hai người đó (làm tròn đến chữ số thập phân thứ ba).
b) Nếu máy bay đáp xuống mặt đất theo đường AM tạo với phương thẳng đứng một góc 100 thì sau 2 phút máy bay đáp xuống mặt đất. Hỏi vận tốc trung bình đáp xuống của máy bay là bao nhiêu km/h? (làm tròn đến chữ số thập phân thứ ba).
 Xem đáp án
Xem đáp án
a)
=> BC = 300.(cot270 + cot250) » 1232,135(m)
b) DAHM vuông, có:
Vận tốc trung bình đáp xuống của máy bay :
Câu 134:
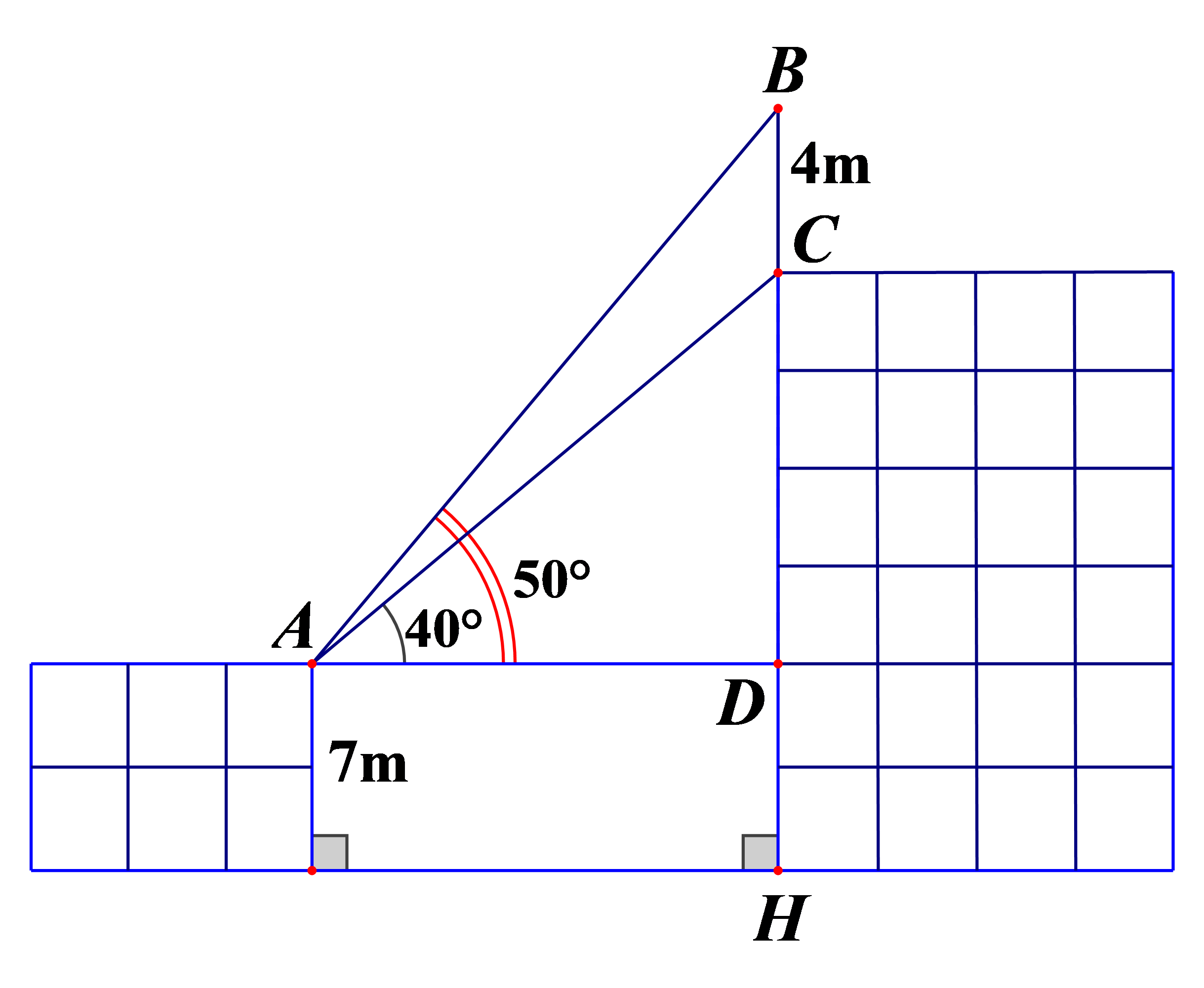
Trên nóc một tòa nhà có một cột ăng-ten thẳng cao 4 m. Từ vị trí quan sát A cao 7 m so với mặt đất có thể nhìn thấy đỉnh B và chân C của cột ăng-ten lần lượt dưới góc 500 và 400 so với phương nằm ngang (trên hình 2). Tính chiều cao CH của tòa nhà (làm tròn đến chữ số thập phân thứ ba).
 Xem đáp án
Xem đáp án
DCAD vuông, có:
Chiều cao CH của tòa nhà: CH = CD + DH = 9,518 + 7= 16,518 (m)
Câu 135:
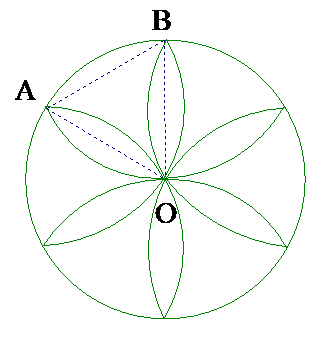
Tính diện tích hình hoa thị 6 cánh tạo bởi 6 cung tròn có bán kính 2 cm và tâm là các đỉnh của lục giác đều nội tiếp đường tròn bán kính 2 cm (làm tròn đến chữ số thập phân thứ nhất).
 Xem đáp án
Xem đáp án
+ Tính diện tích hình quạt (600), diện tích tam giác đều
+ S 1 cánh hoa = 2 ( Sq - SOAB) =
+ S bông hoa = (cm2)
Câu 136:
Minh đi xe đạp từ nhà đến trường với vận tốc 10 km/h hết 12 phút. Khi về, Minh đạp xe với vận tốc 12km/h. Hỏi thời gian Minh đi từ trường về nhà hết bao nhiêu phút?
 Xem đáp án
Xem đáp án
Quãng đường đi từ nhà đến trường:
Thời gian Minh đi từ trường về nhà: 2 : 12 = (phút)
Câu 137:
Các tia nắng mặt trời tạo với mặt đất một góc xấp xỉ bằng 300 và bóng của một tháp trên mặt đất dài 92m. Tính chiều cao của tháp. (Kết quả làm tròn đến chữ số thập phân thứ 2)

 Xem đáp án
Xem đáp án
Gọi h là chiều cao của tháp.
Ta có
Câu 138:
Biết rằng 300g một dung dịch chứa 75g muối. Người ta muốn pha loãng dung dịch đó nên đỗ thêm nước vào để có được một dung dịch chứa 15% muối. Hỏi phải pha thêm bao nhiêu gam nước vào dung dịch đó?
 Xem đáp án
Xem đáp án
Khối lượng dung dịch chứa 15% muối :
Khối lượng nước cần pha thêm : 500 – 300 = 200(g)
Câu 139:
Bạn An ra nhà sách và mang theo một số tiền vừa đủ để mua 10 quyển tập và 6 cây bút. Nhưng khi ra đến nơi, giá một quyển tập mà bạn An định mua đã tăng lên 500 đồng một quyển tập, còn giá một cây bút thì giảm 1000 đồng một cây so với dự định. Vậy để mua 10 quyển tập và 6 cây bút như trên thì bạn An còn thừa hay thiếu số tiền là bao nhiêu?
 Xem đáp án
Xem đáp án
Gọi x(đồng), y(đồng) lần lượt là giá 1 quyển tập và 1 cây cây bút dự định (x>0, y>1000)
Số tiền An mang theo: S1 = 10x + 6y (đồng)
Số tiền An mua trong thực tế: S2 = 10(x + 500) + 6(y – 1000) (đồng)
Ta có S2 = 10x + 5000 + 6y – 6000 = 10x + 6y – 1000 = S1 – 1000
Vậy: để mua 10 quyển tập, 6 cây bút như trên thì bạn An còn thiếu số tiền là 1000 đồng
Câu 140:
Cho rằng diện tích rừng ngập mặn ở xã A được xác định bởi hàm số S = 1320,5 + 13t trong đó S tính bằng héc-ta, t tính bằng số năm kể từ năm 2000. Hãy tính diện tích rừng ngập mặn ở xã A vào các năm 2000 và 2017.
 Xem đáp án
Xem đáp án
S = 1320,5 + 13t
Năm 2000 2017
t 0 17
S 1320,5 1541,5
Câu 141:
Một chiếc máy bay bay lên với vận tốc 600km/h. Đường bay lên tạo với phương nằm ngang một góc 350 (hình bên). Hỏi sau 1 phút máy bay lên cao được bao nhiêu km theo phương thẳng đứng? (làm tròn kết quả đến số thập phân thứ 2)

 Xem đáp án
Xem đáp án
Quãng đường máy bay bay được :
Độ cao máy bay khi đó :
Câu 142:
Giá bán một chiếc xe đạp Martin hiệu M1 ở cửa hàng Martin 107 là hai triệu năm trăm ngàn đồng. Nhân dịp tết dương lịch, cửa hàng Martin 107 khuyến mãi giảm giá 10% tất cả sản phẩm và nếu mua trong khung giờ vàng sẽ được giảm thêm 5% trên giá đã giảm. Bạn A mua xe đạp đó vào dịp khuyến mãi tết dương lịch và mua trong khung giờ vàng. Hỏi bạn A mua xe đạp đó giá bao nhiêu ?
 Xem đáp án
Xem đáp án
Số tiền bạn An mua chiếc xe đạp khi giảm lần 1 (10%):
90% . 2 500 000 = 2 250 000 (đồng)
Số tiền bạn An mua chiếc xe đạp sau 2 lần giảm:
95% . 2 250 000 = 2 137 500 (đồng)
Câu 143:
 Xem đáp án
Xem đáp án
Gọi x(đồng) là số tiền bác Năm đã gửi ngân hàng (x > 0)
Theo đề bài ta có : 104,8%x = 100 400 000 <=> x = 95 801 526,72 (đồng)
Vậy : bác Năm đã gửi ngân hàng số tiền tiết kiệm là 95 801 526,72 đồng
Câu 144:
Biết rằng áp suất nước trên bề mặt đại dương là 1 atmosphere (đơn vị đo áp suất). Khi người thợ lặn sâu xuống thì chịu áp suất của nước biển tăng lên, cứ 10m độ sâu thì áp suất nước biển tăng lên 1 atmosphere. Ở độ sâu d (mét) thì áp suất tăng tương ứng là: với p là áp suất của nước biển và 0 £ d £ 40. Em hãy tính xem nếu người thợ lặn ở độ sâu 15m, 24m trong đại dương thì chịu tác dụng của áp suất của nước biển là bao nhiêu?
 Xem đáp án
Xem đáp án
d = 15 => (atmosphere)
d = 24 => (atmosphere)
Câu 145:
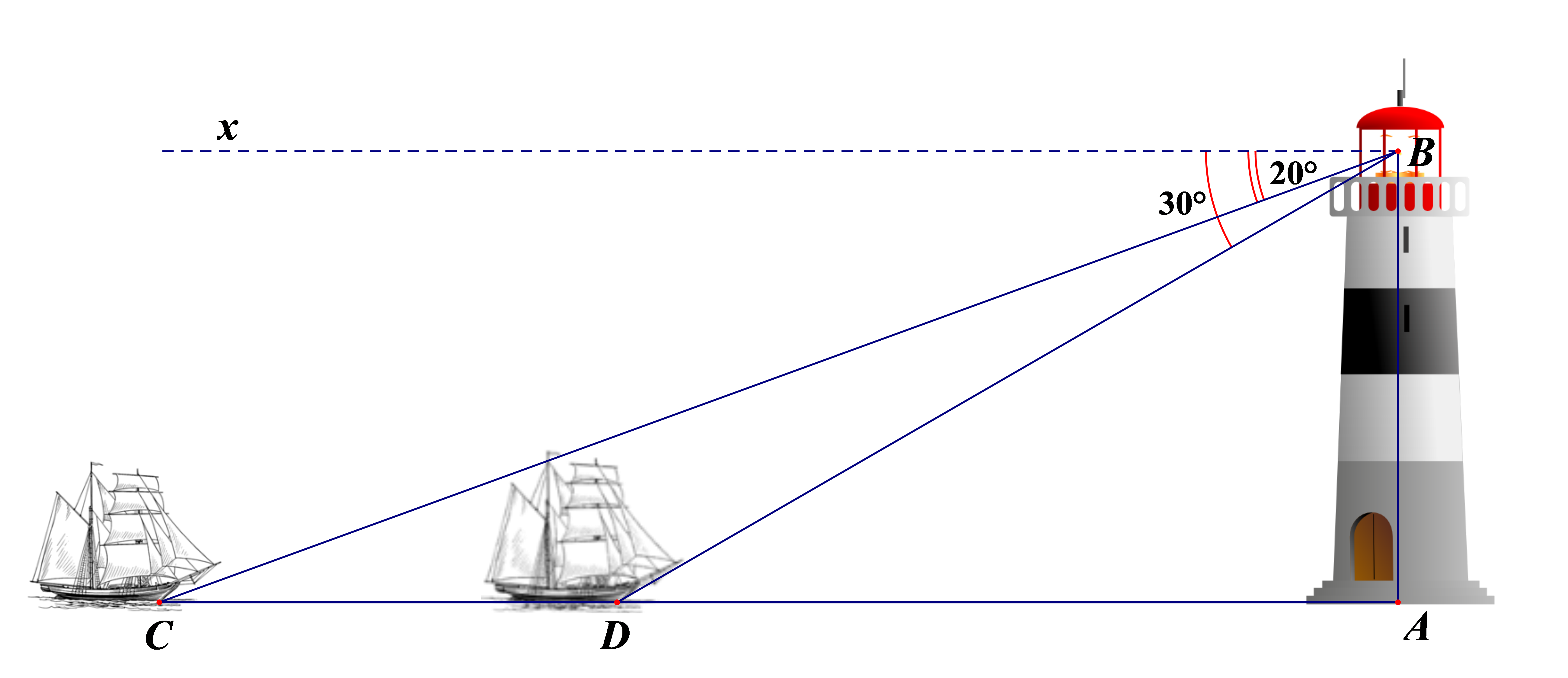
Một người đứng trên tháp quan sát của ngọn hải đăng cao 50m nhìn về hướng Tây Nam, người đó quan sát hai lần một con thuyền đang hướng về ngọn hải đăng. Lần thứ nhất người đó nhìn thấy thuyền với góc hạ là 200, lần thứ 2 người đó nhìn thấy thuyền với góc hạ là 300. Hỏi con thuyền đã đi được bao nhiêu mét giữa hai lần quan sát (làm tròn hai chữ số thập phân).
 Xem đáp án
Xem đáp án
(so le trong) ; (so le trong)
Vậy : giữa hai lần quan sát , con thuyền đã đi được 50,77 m.
Câu 146:
Một miếng đất hình chữ nhật có chiều dài 90m và chiều rộng là 50m. Người ta chia miếng đất ra thành những miếng đất nhỏ hình vuông để trồng từng loại rau trên từng miếng hình vuông đó. Hỏi số hình vuông được chia ít nhất là bao nhiêu?
 Xem đáp án
Xem đáp án
Số hình vuông được chia ít nhất có cạnh hình vuông lớn nhất
Cạnh hình vuông lớn nhất là ƯCLN(90 ; 50)
90 = 2 . 32 . 5 ; 50 = 2 . 52 Þ ƯCLN(90 ; 50) = 2 . 5 = 10
Số hình vuông được chia ít nhất là (90 . 50) : 102 = 45 (hình vuông)
Câu 147:
Một hình chữ nhật có kích thước là 40 cm và 30 cm. Nếu tăng mỗi kích thước của hình đó thêm x(cm) thì được hình chữ nhật mới có chu vi là y(cm).
a) Hãy lập công thức tính y theo x.
 Xem đáp án
Xem đáp án
a) y = 2(40 + x + 30 + x) = 4x + 140
Câu 148:
b) Tính chu vi hình chữ nhật khi x = 5 (cm)
 Xem đáp án
Xem đáp án
b) x = 5 Þ y = 4 . 5 + 140 = 160(cm)
Câu 149:
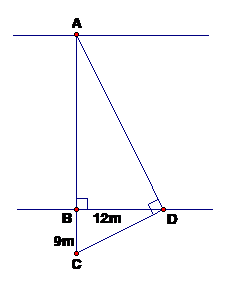
Hãy tính ciều rộng AB của một con sông (hình vẽ). Biết rằng BC = 9m, BD = 12m.
 Xem đáp án
Xem đáp án
BD2 = AB.BC (HTL trong tam giác vuông)
Þ 122 = AB.9 Þ AB = 16(m)
Câu 150:
Hải đăng Đá Lát là một trong 7 ngọn Hải đăng cao nhất Việt Nam, được đặt trên đảo Đá Lát ở vị trí cực Tây Quần đảo, thuộc xã đảo Trường Sa, huyện Trường Sa, tỉnh Khánh Hòa. Ngọn hải đăng được xây dựng năm 1994, cao 42 mét, có tác dụng chỉ vị trí đảo, giúp tàu thuyền hoạt động trong vùng biển Trường Sa định hướng và xác định được vị trí mình. Một người đi trên tàu đánh cá muốn đến ngọn hải đăng Đá Lát, người đó đứng trên mũi tàu cá và dùng giác kế đo được góc giữa mũi tàu và tia nắng chiếu từ đỉnh ngọn hải đăng đến tàu là 100.
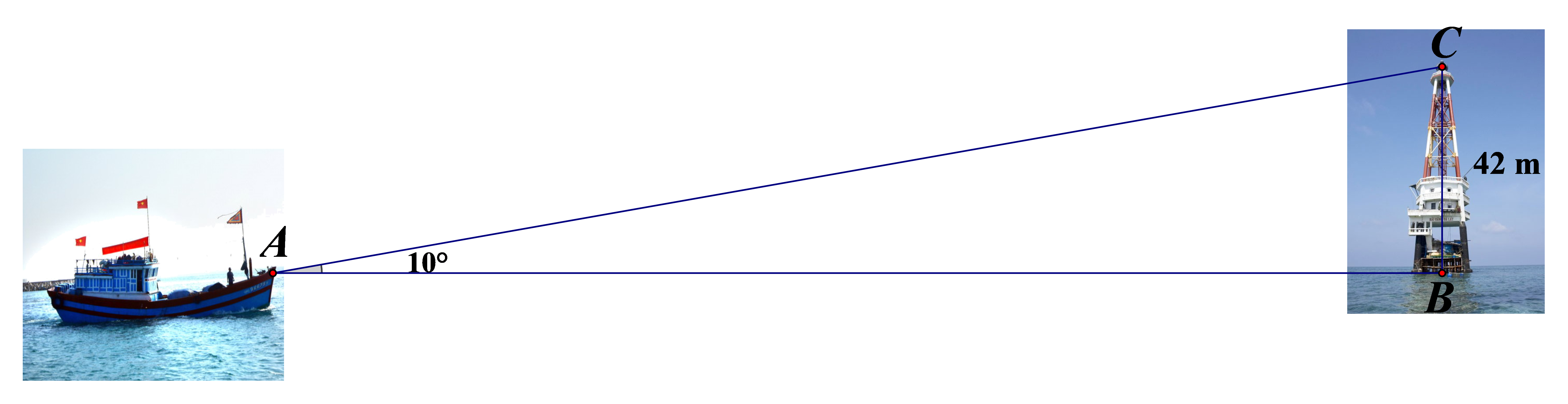
a) Tính khoảng cách từ tàu đến ngọn hải đăng. (làm tròn đến 1 chữ số thập phân)
b) Biết cứ đi 10 m thì tàu đó hao tốn hết 0,02 lít dầu. Hỏi tàu đó để đi đến ngọn hải đăng Đá Lát cần tối thiểu bao nhiêu lít dầu?
 Xem đáp án
Xem đáp án
a)
b)
Số dầu cần tối thiểu :
Câu 151:
Nhân ngày “Phụ nữ Việt Nam 20/10”, cửa hàng bán túi xách và ví da giảm giá 30% cho tất cả các sản phẩm và ai có thẻ “khách hàng thân thiết” sẽ được giảm tiếp 10% trên giá đã giảm.
a) Hỏi mẹ bạn An có thẻ khách hàng thân thiết khi mua 1 cái túi xách trị giá 500000 đồng thì phải trả bao nhiêu tiền?
 Xem đáp án
Xem đáp án
a) Số tiền mẹ bạn An mua 1 túi xách khi giảm lần 1: 70% . 500 000 = 350 000 (đồng)
Số tiền mẹ bạn An mua 1 túi xách sau 2 lần giảm: 90% . 350 000 = 315 000 (đồng)
Câu 152:
b) Mẹ bạn An mua túi xách trên và thêm 1 cái bóp nên trả tất cả 693000 đồng. Hỏi giá ban đầu của cái bóp là bao nhiêu?
 Xem đáp án
Xem đáp án
b) Số tiền mua bóp : 693 000 – 315 000 = 378 000 (đồng)
Gọi x(đồng) là giá 1 cái bóp ban đầu
Số tiền mẹ bạn An mua 1 cái bóp khi giảm lần 1: 70%x = 0,7x (đồng)
Số tiền mẹ bạn An mua 1 cái bóp sau 2 lần giảm: 90%.0,7x = 0,63x (đồng)
Ta có 0,63x = 378 000 <=> x = 600 000 (đồng)
Câu 153:
Nam và Hùng nhận gia công hàng mỹ nghệ. Ngày thứ nhất họ làm ra được 01 sản phẩm; Ngày thứ hai họ làm ra được 03 sản phẩm; Ngày thứ ba số sản phẩm họ làm ra bằng số sản phẩm ngày thứ hai cộng thêm hai (là 05 sản phẩm). Số sản phẩm ngày thứ tư bằng số sản phẩm ngày thứ ba cộng thêm hai.
Hỏi theo quy luật đó, sau đợt gia công Nam và Hùng tạo ra tất cả bao nhiêu sản phẩm biết ngày cuối cùng họ tạo ra được 49 sản phẩm?
 Xem đáp án
Xem đáp án
Theo quy luật trên, ta thấy Nam và Hùng mỗi ngày làm được số sản phẩm là số lẻ và ngày sau hơn ngày trước 2 sản phẩm
Số sản phẩm làm được : T = 1 + 3 + 5 + . . . + 49
Số số hạng : (49 – 1) : 2 + 1 = 25
T = (49 + 1).25 : 2 = 625 (sản phẩm)
Câu 154:
 Xem đáp án
Xem đáp án
Giá bán 1 tivi khi giảm lần 1: 50% . 6 500 000 = 3 250 000 (đồng)
Giá bán 1 tivi khi giảm lần 2: 90% . 3 250 000 = 2 925 000 (đồng)
Số tiền bán được 40 tivi: (20 . 3 250 000) + (20 . 2 925 000) = 123 500 000 (đồng)
Số tiền vốn của 40 tivi: 40 . 3 050 000 = 122 000 000 (đồng) < 123 500 000 (đồng)
Vậy: cửa hàng đó lời khi bán hết lô hàng tivi
Câu 155:
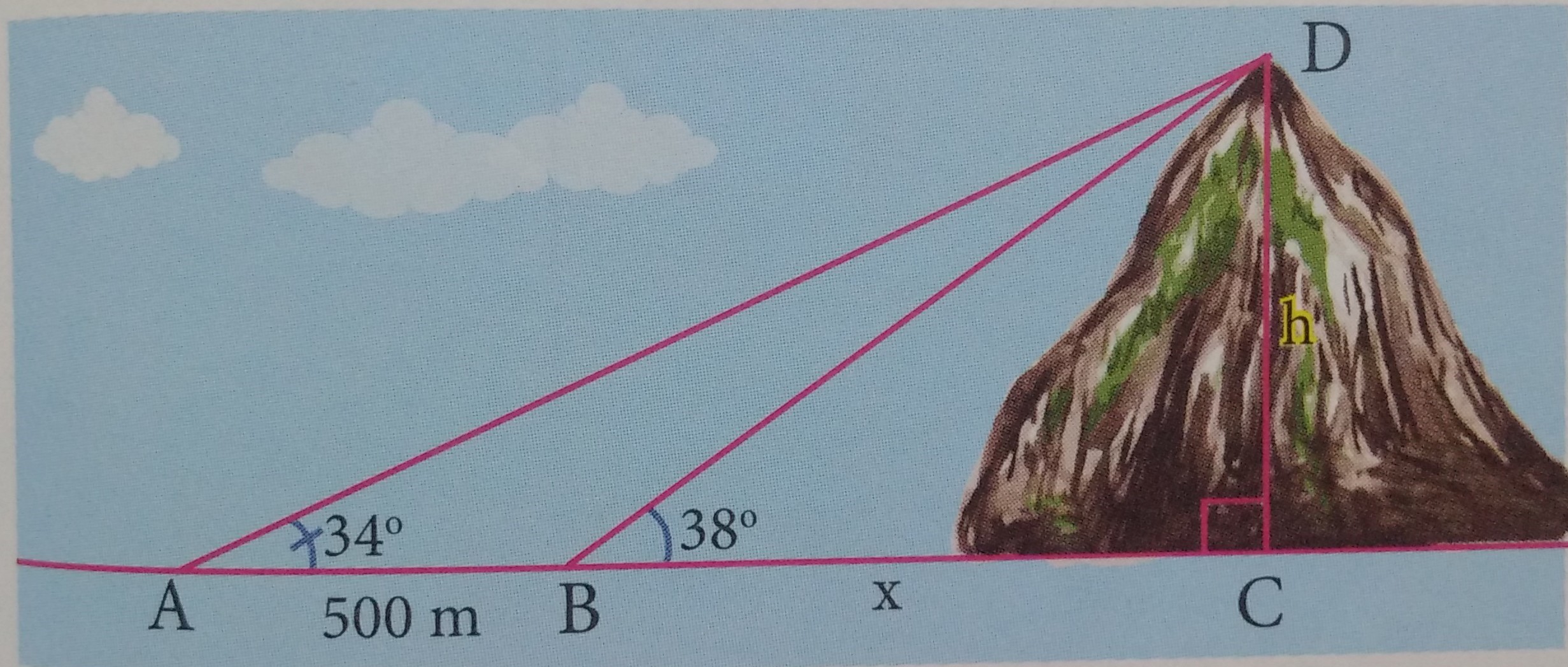
 Xem đáp án
Xem đáp án
Vậy: Chiều cao của ngọn núi là 2468m
Câu 156:
Hiện nay tại nước Mỹ quy định cầu thang cho người khuyết tật dùng xe lăn có hệ số góc không quá . Để phù hợp với tiêu chuẩn ấy thì chiều cao của cầu thang tối đa là bao nhiêu khi biết đáy cầu thang có độ dài là 4m ?
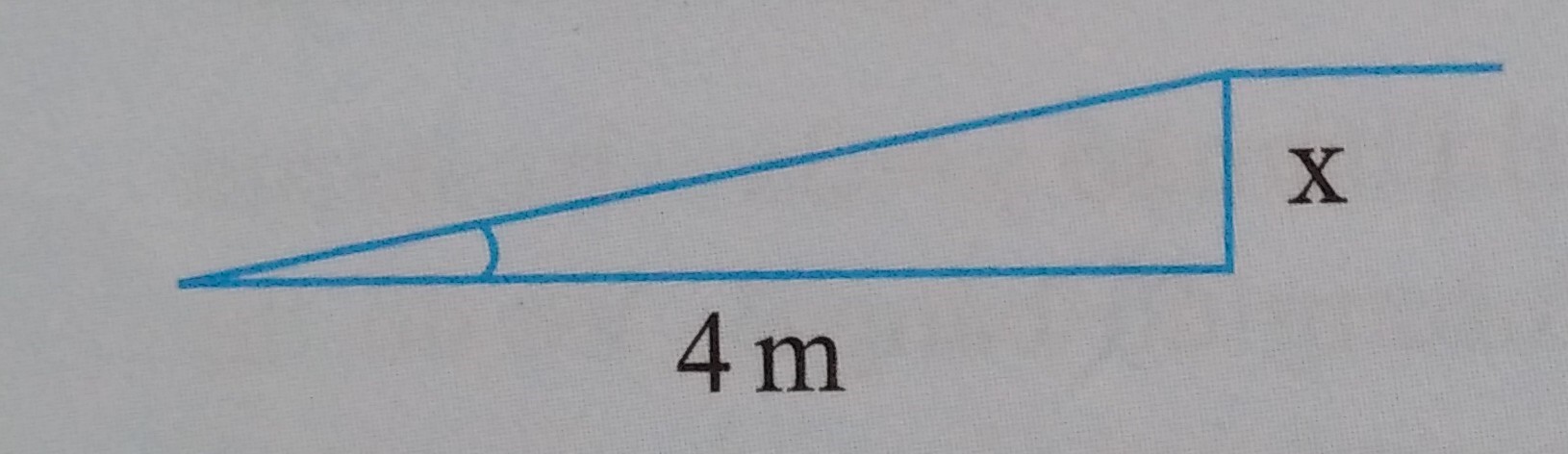
 Xem đáp án
Xem đáp án
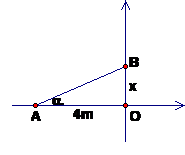
Đặt bài toán vào hệ trục tọa độ, ta có hình vẽ sau:
(m)
Vậy: chiều cao của cầu thang tối đa là ![]() (m)
(m)
Câu 157:
Một máy bay cất cánh theo phương có góc nâng là 230 so với mặt đất. Hỏi muốn đạt độ cao 250m so với mặt đất thì máy bay phải bay lên một đoạn đường là bao nhiêu mét? (làm tròn đến mét)
 Xem đáp án
Xem đáp án
Theo đề bài ta có hình vẽ sau:
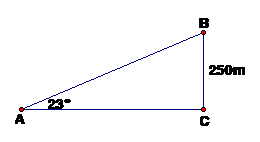
Vậy: máy bay phải bay lên một đoạn đường là 640m
Câu 158:
Một hỗn hợp dung dịch gồm nước và muối trong đó có 6% muối (về khối lượng). Hỏi phải thêm bao nhiêu kg nước vào 50kg dung dịch trên để có được một dung dịch mới có 3% muối.
 Xem đáp án
Xem đáp án
Khối lượng muối có trong dung dịch: mct = mdd . C% = 50 . 6% = 3(kg)
Khối lượng dung dịch mới có 3% muối :
Khối lượng nước cần thêm : 100 – 50 = 50(kg)
Câu 159:
Một cửa hàng có hai loại quạt, giá tiền như nhau. Quạt màu xanh được giảm giá hai lần, mỗi lần giảm giá 10% so với giá đang bán. Quạt màu đỏ được giảm giá một lần 20%. Hỏi sau khi giảm giá như trên thì loại quạt nào rẻ hơn.
 Xem đáp án
Xem đáp án
Gọi x là giá tiền ban đầu của hai loại quạt
Giá tiền quạt xanh sau khi giảm lần 1: 90%x = 0,9x
Giá tiền quạt xanh sau khi giảm lần 2: 90% . 0,9x = 0,81x
Giá tiền quạt đỏ sau khi giảm 20%: 80%x = 0,8x < 0,81x
Vậy: loại quạt xanh rẻ hơn loại quạt đỏ.
Câu 160:
 Xem đáp án
Xem đáp án
Căn hộ của Vy ở tầng thứ: [(135 – 30) : 21] + 1 = 6
Câu 161:
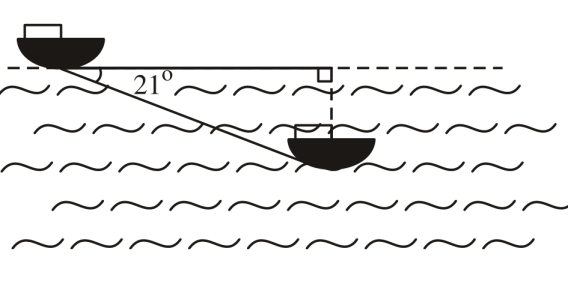
Tàu ngầm đang ở trên mặt biển bỗng đột ngột lặn xuống theo phương tạo với mặt nước biển một góc 210. Nếu tàu chuyển động theo phương lặn xuống được 300m thì nó ở độ sâu bao nhiêu? Khi đó khoảng cách theo phương nằm ngang so với nơi xuất phát là bao nhiêu m? ( kết quả làm tròn đến m)
 Xem đáp án
Xem đáp án
Theo đề bài ta có hình vẽ sau:

Tàu ở độ sâu :
Khoảng cách so với nơi xuất phát :
Câu 162:
Một sân bóng đá nhân tạo có chu vi là 50m. Tính khoảng cách từ gốc phạt góc đến đường chéo của sân bóng đá biết chiều dài và chiều rộng tỉ lệ với 3 :2 (làm tròn 2 chữ số thập phân). (Hình dưới)
 Xem đáp án
Xem đáp án
Gọi x(m), y(m) lần lượt là chiều dài, chiều rộng của hình chữ nhật (x, y > 0)
Theo đề bài ta có:
và 2(x + y) = 50
=> và x + y = 25
Áp dụng tính chất của dãy tỉ số bằng nhau:
=> x = 15 ; y = 10
Þ AB = 15(m) ; AD = 10(m)
Ta có (HTL trong tam giác vuông)
=> AH » 8,32(m)
Vậy: khoảng cách từ gốc phạt góc đến đường chéo của sân bóng đá là 8,32 m
Câu 163:
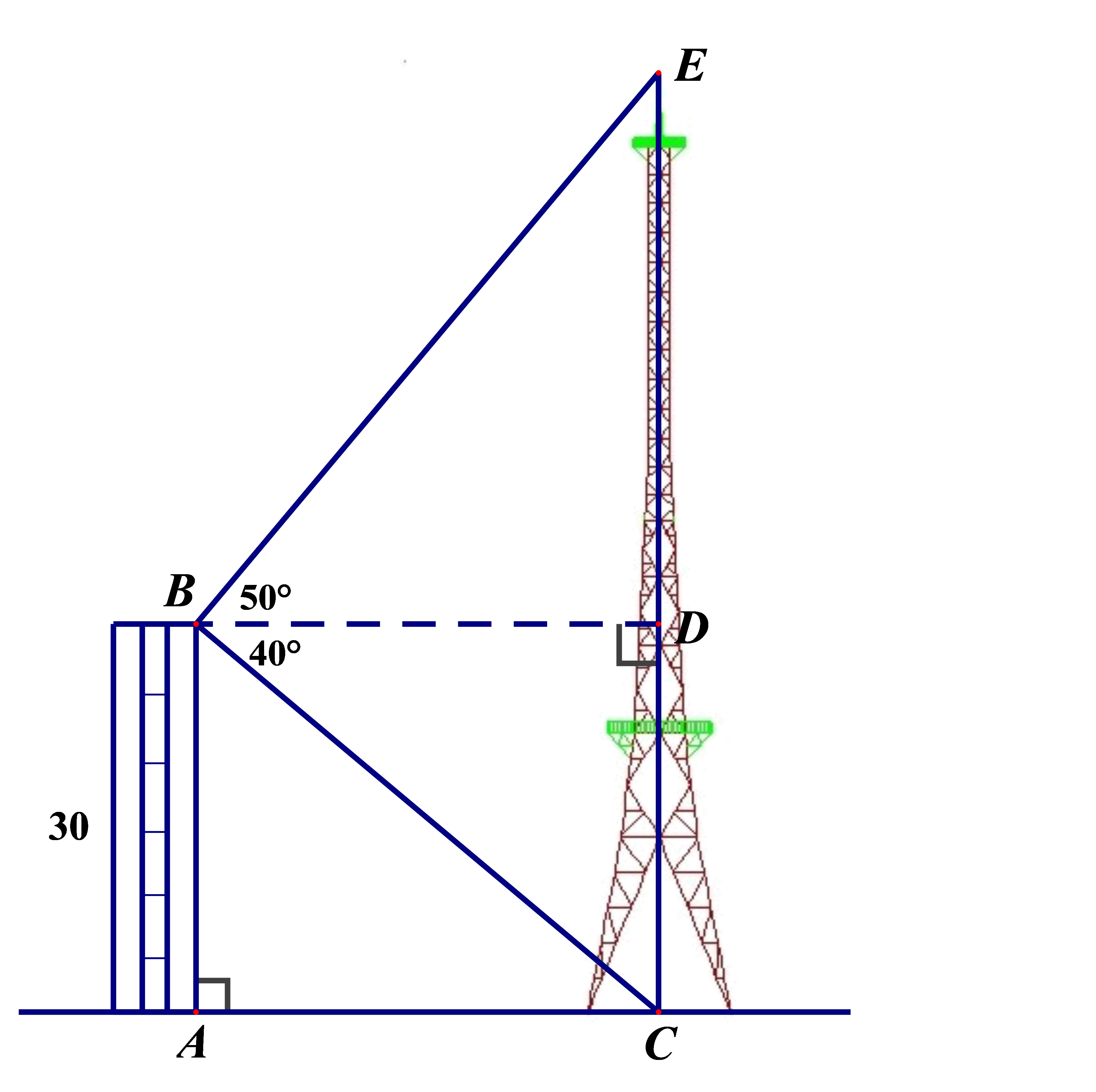
 Xem đáp án
Xem đáp án
AB = CD = 30m
DBDC vuông, có :
BC2 = CD.CE (HTL trong tam giác vuông)
472 = 30 . CE Þ CE » 74(m)
Vậy: chiều cao của cột ăng-ten là 74 m
Câu 164:
Trong vườn sinh học của nhà trường, các em trong CLB Sinh học có thu hoạch được một số kilôgam (kg) cải Hà Lan và cải Newzealand. Trong đó 70% là cải Hà Lan, còn lại là cải Newzealand. Khối lượng cải Hà Lan nhiều hơn khối lượng cải Newzealand là 30 kg. Giá mỗi kg cải Hà Lan là 30 000 đồng, giá mỗi kg cải Newzealand là 20 00 đồng. Hỏi các em trong CLB sinh học bán được bao nhiêu tiền từ số kg cải thu hoạch được ?
 Xem đáp án
Xem đáp án
Gọi x(kg) là khối lượng của cải Newzealand (x > 0)
Khối lượng của cải Hà Lan là x + 3 (kg)
Vì 70% là cải Hà Lan, nên ta có :
70%(x + x + 30) = x + 30 Û x = 225 (nhận)
Do đó số cải thu hoạch : Newzealand : 22,5 (kg)
Hà Lan : 22,5 + 30 = 52,5 (kg)
Số tiền bán được: (22,5 . 20 000) + (52,5 . 30 000) = 2 025 000 (đồng)
Câu 165:
Tính từ năm 2000 đến nay, cả nước đã tiến hành 3 cuộc tổng điều tra đất đai (năm 2000, 2005 và 2010). Theo kết quả của 3 cuộc tổng điều tra này thì diện tích đất nông nghiệp nước ta được biểu diễn theo công thức S = 0,12t + 8,97 trong đó diện tích S tính bằng triệu héc-ta, t tính bằng số năm kể từ năm 2000.
a) Hỏi vào năm 2000 diện tích đất nông nghiệp nước ta là bao nhiêu?
 Xem đáp án
Xem đáp án
a) S = 0,12t + 8,97
Năm 2000 diện tích đất nông nghiệp nước ta là :
S = 0,12(2000 – 2000) + 8,97 = 8,97 (héc-ta)
Câu 166:
 Xem đáp án
Xem đáp án
Diện tích đất nông nghiệp nước ta đạt 10,05 triệu héc-ta, nên ta có:
10,05 . 106 = 0,12t + 8,97 <=> t = 9
Vậy: năm đó là năm 2009
Câu 167:

 Xem đáp án
Xem đáp án
Quãng đường máy bay bay được: AC = (km)
Máy bay lên độ cao:
Câu 168:
Nhà bạn Bình có gác lửng cao so với nền nhà là 3m. Ba bạn Bình cần đặt một thang đi lên gác, biết khi đặt thang phải để thang tạo được với mặt đất một góc 700 thì đảm bảo sự an toàn khi sử dụng. Với kiến thức đã học Bình hãy giúp Ba bạn tính chiều dài thang bao nhiêu mét để sử dụng. (kết quả làm tròn đến chữ số thập phân thứ nhất)
 Xem đáp án
Xem đáp án
Theo đề bài ta có hình ảnh sau:
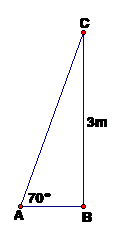
Vậy: thang cần sử dụng là 3,2 m
Câu 169:
Tháng 11 vừa qua, có ngày Black Friday, phần lớn các trung tâm thương mại đều giảm giá rất nhiều mặt hàng. Mẹ bạn An có dẫn An đến một trung tâm thương mại để mua một đôi giày. Biết đôi giày đang khuyến mãi giảm giá 40%, mẹ An có thẻ khách hàng thân thiết của trung tâm thương mại nên được giảm thêm 5% trên giá đã giảm nữa, do đó mẹ An chỉ phải trả 684.000 đồng cho đôi giày. Hỏi giá bán ban đầu của đôi giày nếu không khuyến mãi là bao nhiêu?
 Xem đáp án
Xem đáp án
Gọi x(đồng) là giá bán ban đầu của đôi giày (x > 0)
Giá bán của đôi giày khi giảm lần 1: 60%x = 0,6x (đồng)
Giá bán của đôi giày khi giảm lần 2: 95% . 0,6x = 0,57x (đồng)
Theo đề bài ta có: 0,57x = 684000 <=> x = 1 200 000 (nhận)
Vậy: giá bán ban đầu của đôi giày nếu không khuyến mãi là 1 200 000 đồng.
Câu 170:
Một cửa hàng nhập về nhãn hàng máy tính xách tay với giá vốn là 4500000 đồng. Cửa hàng dự định công bố giá niêm yết (giá bán ra) là 6000000 đồng.
a) Nếu bán với giá niêm yết trên thì cửa hàng lãi bao nhiêu phần trăm so với giá vốn?
 Xem đáp án
Xem đáp án
a) Tỉ lệ phần trăm cửa hàng lãi so với giá vốn là:
Câu 171:
b) Để có lãi ít nhất 5% thì cửa hàng có thể giảm giá nhiều nhất bao nhiêu phần trăm?
 Xem đáp án
Xem đáp án
b) Giá bán của cửa hàng khi lãi 5% là: 4 500 000 . 105% = 4 725 000 (đồng)
Tỉ lệ phần trăm của giá mới so với giá niêm yết là:
Vậy: cửa hàng có thể giảm giá nhiều nhất là: 100% – 78,75% = 21,25%
Câu 172:
Một chiếc flycam (thiết bị bay điều khiển từ xa dùng để chụp ảnh và quay phim từ trên không) đang ở vị trí A cách chiếc cầu BC (theo phương thẳng đứng) một khoảng AH = 120m. Biết góc tạo bởi AB, AC với các phương vuông góc với mặt cầu tại B, C theo thứ tự là . Tính chiều dài BC của cây cầu. (Làm tròn kết quả đến chữ số thập phân thứ hai).
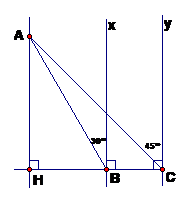
 Xem đáp án
Xem đáp án
Vậy : Chiều cao BC của cây cầu là 76,32 m.
Câu 173:
Năm nay số dân ở một thành phố A có 2 000 000 người. Hỏi 2 năm sau số dân ở thành phố A là bao nhiêu người? Biết rằng bình quân mỗi năm số dân ở một thành phố A này tăng 0,5%.
 Xem đáp án
Xem đáp án
Số dân ở thành phố A sau 1 năm: 2 000 000 . 100,5% = 2 010 000 (người)
Số dân ở thành phố A sau 2 năm: 2 010 000 . 100,5% = 2 020 050 (người)
Câu 174:
Các tia sáng mặt trời tạo tạo với mặt đất một góc xấp xỉ 300. Tại thời điểm đó bóng của một cái cây trên mặt đất dài 20m. Hỏi cái cây đó cao bao nhiêu mét? (làm tròn tới phần thập phân thứ nhất)
 Xem đáp án
Xem đáp án
Theo đề bài ta có hình vẽ sau:
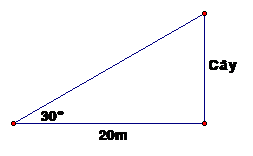
Vậy: cây cao 11,5 m
Câu 175:
 Xem đáp án
Xem đáp án
Theo đề bài ta có hình vẽ sau:
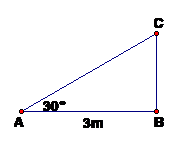
BC + AC = 1,7 + 3,5 = 5,2 (m)
Vậy: lúc đầu cây Hoài Nam cao 5,2(m)
Câu 176:
Gia đình bạn Hân đi siêu thị Điện Máy Xanh mua một món hàng đang khuyến mãi được giảm giá 10%. Do mẹ bạn có thể VIP của siêu thị nên được giảm thêm 5% trên giá đã giảm. Vì thế, gia đình bạn chỉ phải trả 14 535 000 đồng cho món hàng đó. Hỏi giá tiền ban đầu của món hàng nếu không khuyến mãi là bao nhiêu?
 Xem đáp án
Xem đáp án
Gọi x(đồng) là giá bán ban đầu của món hàng (x > 0)
Giá bán của món hàng khi giảm lần 1: 90%x = 0,9x (đồng)
Giá bán của món hàng khi giảm lần 2: 95% . 0,9x = 0,855x (đồng)
Theo đề bài ta có: 0,855x = 14 535 000 <=> x = 17 000 000 (nhận)
Vậy: giá bán ban đầu của món hàng nếu không khuyến mãi là 17 000 000 đồng.
Câu 177:
Ông A gửi tiền vào ngân hàng kì hạn 12 tháng với lãi suất 6,5%. Đúng một năm ông A nhận được cả vốn lẫn lãi là 53 250 000 đồng. Hỏi tiền vốn lúc đầu của ông A là bao nhiêu ?
 Xem đáp án
Xem đáp án
Gọi x(đồng) là số tiền vốn lúc đầu của ông A (x > 0)
Theo đề bài ta có: 106,5%.x = 53 250 000 <=> x = 50 000 000 (nhận)
Vậy: tiền vốn lúc đầu của ông A là 50 000 000 đồng.
Câu 178:
Một chiếc thang dài 3m. Cần đặt chân thang cách chân tường một khoảng cách bằng bao nhiêu để nó tạo với mặt đất một góc “an toàn” 650 (tức đảm bảo thang không bị đổ khi sử dụng)? (kết quả làm tròn đến chữ số thập phân thứ 2)

 Xem đáp án
Xem đáp án
Theo đề bài ta có hình vẽ sau:
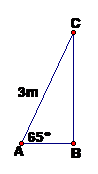
Vậy: Cần đặt chân thang cách chân tường một khoảng 1,27 m
Câu 179:
Một quả bóng tròn có đường kính 30cm, một bóng đèn đặt cách tâm quả bóng 25cm. Tính khoảng cách xa nhất trên quả bóng mà ánh sáng của bóng đèn có thể chiếu tới.
 Xem đáp án
Xem đáp án
Theo đề bài ta có hình vẽ sau:
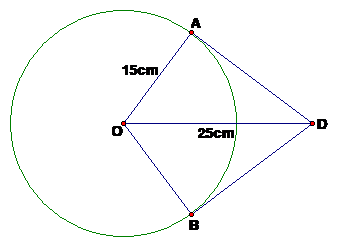
OA = 30 : 2 = 15(cm)
(DA là tiếp tuyến của (O))
DA2 = AD2 – OA2 (định lý Pytago)
DA2 = 252 – 152
DA = 20(cm)
Vậy: khoảng cách xa nhất trên quả bóng mà ánh sáng của bóng đèn có thể chiếu tới là 20 m
Câu 180:
Hãy tính chiều cao AH của tòa nhà ở hình bên cạnh. (làm tròn đến hàng đơn vị)
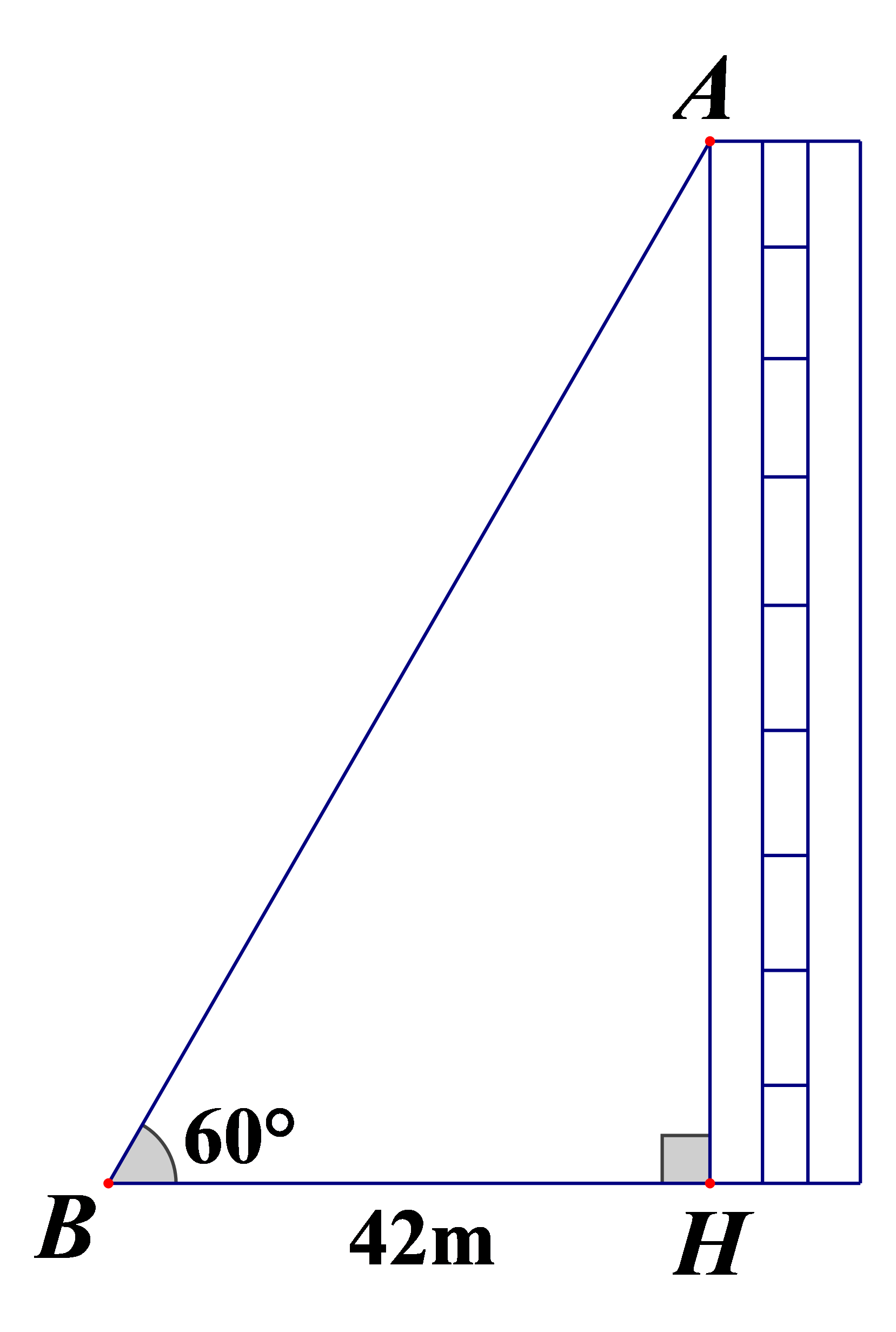
 Xem đáp án
Xem đáp án
Vậy: chiều cao AH của tòa nhà là 73 m
Câu 181:
Cửa hàng Hoàng Ân chuyên bán quần áo thời trang cao cấp dành cho nữ tuổi teen. Ngày thứ sáu đen (Black Friday) 24/11/2017, ngày siêu giảm giá không chỉ diễn ra ở Mỹ mà còn là ngày hội bán hàng của các doanh nghiệp ở Việt Nam. Để chuẩn bị cho ngày này, của hàng Hoàng Ân đã dành một số áo và giảm giá 50% cho mọi sản phẩm. Sau đây là cách chọn size áo (cỡ áo) của nữ theo thông số cân nặng và chiều cao:
|
Chiều cao |
1,48m-1,53m |
1,53m-1,55m |
1,53m-1,58m |
1,55m-1,62m |
1,55m-1,66m |
|
Cân nặng |
38kg - 43kg |
43kg - 46kg |
46kg - 53kg |
53kg - 57kg |
57kg - 66kg |
|
Chọn size |
S |
M |
L |
XL |
XXL |
Tổng số áo có size S và size M là 390 áo đã được bán hết và có tỷ lệ lần lượt là 60% và ![]() trên tổng số áo đã bán của ngày 24/11/2017. Hỏi số áo đã bán của ngày thứ sáu đen 24/11/2017 của cửa hàng Hoàng Ân là bao nhiêu áo?
trên tổng số áo đã bán của ngày 24/11/2017. Hỏi số áo đã bán của ngày thứ sáu đen 24/11/2017 của cửa hàng Hoàng Ân là bao nhiêu áo?
 Xem đáp án
Xem đáp án
Gọi a (áo) là số đã bán của cửa hàng
Và x (áo) là số áo size S đã bán
Số áo size M đã bán là 390 – x (áo)
Theo đề bài ta có:
x = 60%a = 0,6a (1) ; (2)
Thay (1) vào (2): 390 – 0,6a = 0,375ª Û a = 400
Vậy: số áo đã bán của ngày thứ sáu đen 24/11/2017 của cửa hàng Hoàng Ân là 400 áo
Câu 182:
Biết rằng trong 500g dung dịch nước muối có chứa 150g muối nguyên chất. Hỏi cần phải cho thêm vào dung dịch đó bao nhiêu gam nước để dung dịch có nồng độ là 20%.
 Xem đáp án
Xem đáp án
Khối lượng dung dịch có nồng độ là 20%:
Khối lượng nước cần pha thêm:
750 – 500 = 250(g)
Câu 183:
Hai bạn A và B đứng ở hai đầu bờ hồ cùng nhìn về một cậy (gốc là điểm C). Biết góc nhìn tại A của bạn A là 510, góc nhìn tại B của bạn B là 300, và khoảng cách từ A đến C là 224 m, khoảng cách từ B đến C là 348 m. Hỏi hai bạn A và B đứng cách nhau bao nhiêu mét? (làm tròn mét)
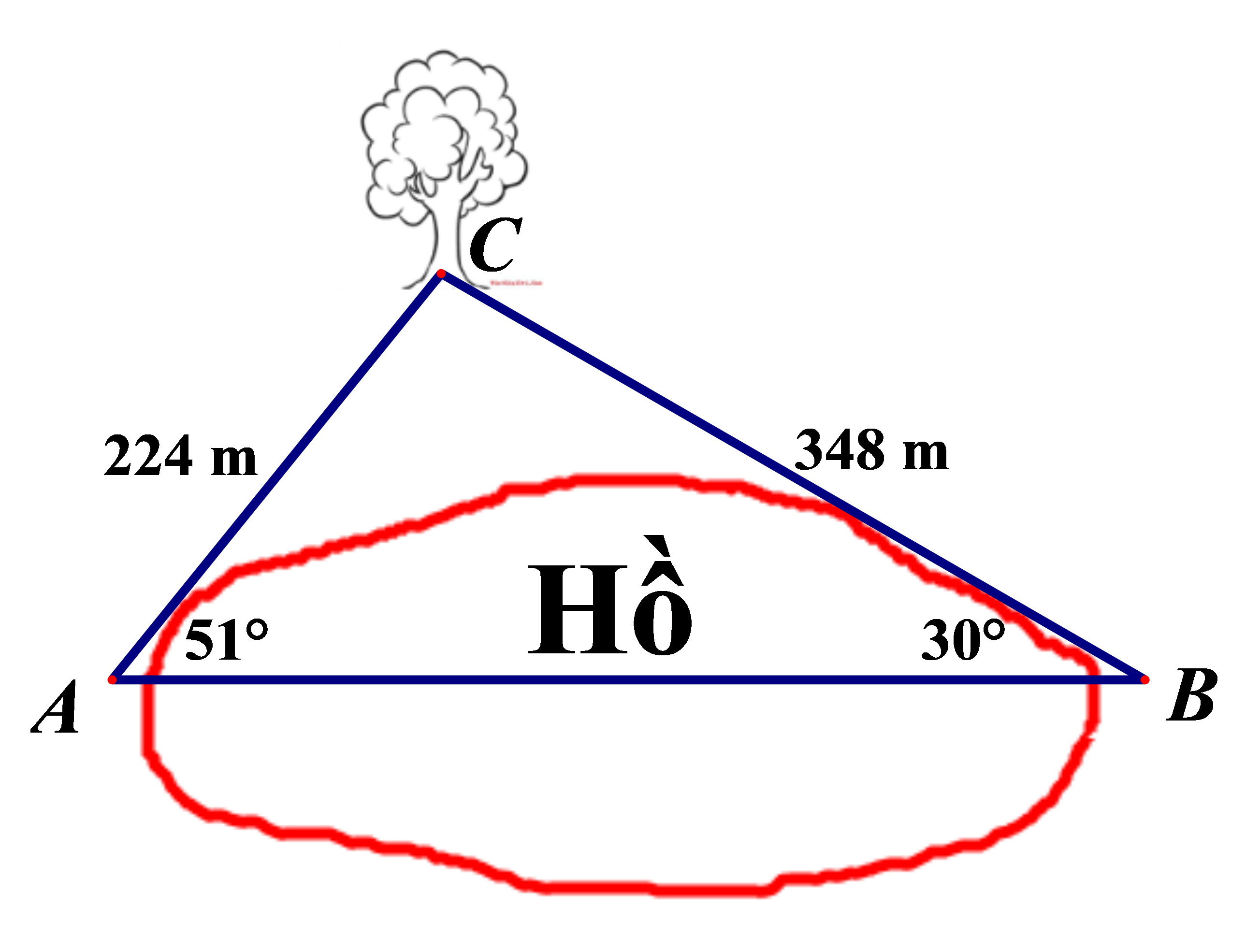
 Xem đáp án
Xem đáp án
Theo đề bài ta có hình vẽ sau
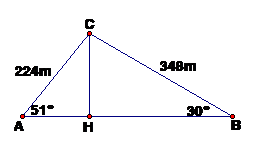
AB = AH + BH = 141 + 301 = 442(m)
Vậy: hai bạn A và B đứng cách nhau 442Câu 184:
Một người gửi vào ngân hàng với số tiền là 200 000 000 với lãi suất là 6%/1 năm. Sau 3 năm người đó đến ngân hàng rút tiền thì được bao nhiêu tiền cả gốc lẫn lãi (biết rằng số tiền lãi mỗi năm, nếu không rút thì được cộng vào vốn để tính lãi cho năm tiếp theo).
 Xem đáp án
Xem đáp án
Số tiền vốn và lãi sau 1 năm: 200 000 000 . 106% = 212 000 000 (đồng)
Số tiền vốn và lãi sau 2 năm: 212 000 000 . 106% = 224 720 000 (đồng)
Số tiền vốn và lãi sau 3 năm: 224 720 000 . 106% = 238 203 200 (đồng)
Câu 185:
Một cây cột đèn cao 9m có bóng trải dài trên mặt đất là 5m. Hãy tính góc (làm tròn đến độ) mà tia sáng mặt trời tạo với mặt đất vào thời điểm đó.
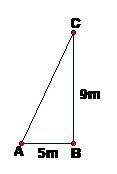
 Xem đáp án
Xem đáp án
Theo đề bài ta có hình vẽ sau:
Câu 186:
Rừng ngập mặn Cần Giờ (còn gọi là Rừng Sác), trong chiến tranh bom đạn và chất độc hóa học đã làm nơi đây trở thành “vùng đất chết” ; được trồng lại từ năm 1979, nay đã trở thành “lá phổi xanh” cho Thành phố Hồ Chí Minh, được UNESCO công nhận là Khu dự trữ sinh quyên của thế giới đầu tiên ở Việt Nam vào ngày 21/01/2000. Diện tích rừng phủ xanh được cho bởi hàm số S = 3,14 + 0,05t trong đó S tính bằng nghìn héc-ta, t tính bằng số năm kể từ năm 2000. Hãy tính điện tích Rừng Sác được phủ xanh vào các năm 2000 và 2017.
 Xem đáp án
Xem đáp án
S = 3,14 + 0,05t
Năm 2000 2017
t 0 17
S 3,14 3,99
Câu 188:
Để chuẩn bị làm bánh nhân dịp Noel, bạn An muốn mua một khay nướng và một bộ khuôn tạo hình. Hai cửa hàng A và B ở cạnh nhau, cùng bán hai món đồ bạn An muốn mua với giá như nhau: khay nướng giá 280 000 đồng/cái và bộ khuôn tạo hình giá 75 000 đồng/bộ. Tuy nhiên, hai cửa hàng lại có hai hình thức khuyến mãi khác nhau.
Cửa hàng A: khay nướng được giảm giá 10% và bộ khuôn tạo hình được giảm giá 20%.
Cửa hàng B: Tất cả sản phẩm đều được giảm giá 15%.
Hỏi bạn An nên mua ở cửa hàng nào để có lợi hơn?
 Xem đáp án
Xem đáp án
Số tiền mua một khay nướng và một bộ khuôn tạo hình ở cửa hàng A:
(90% . 280 000) + (80% . 75 000) = 312 000 (đồng)
Số tiền mua một khay nướng và một bộ khuôn tạo hình ở cửa hàng B:
85% (280 000 + 75 000) = 301 750 (đồng)
Vậy: bạn An nên mua ở cửa hàng B để có lợi hơn.
