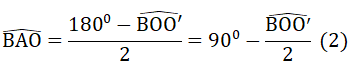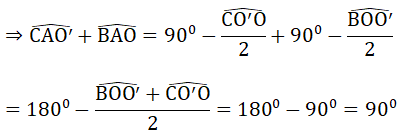Đề kiểm tra 1 tiết Toán 9 Chương 2 Hình học có đáp án
-
514 lượt thi
-
11 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Phần trắc nghiệm
Nội dung câu hỏi 1
Chọn khẳng định đúng.
Tâm của đường tròn đi qua ba điểm phân biệt A, B, C phân biệt không thẳng hàng là giao điểm của:
Xem đáp án
Đáp án là C
Câu 2:
Cho AB và AC là 2 tiếp tuyến của (O) với B, C là các tiếp điểm. Câu trả lời nào sau đây là sai?
Xem đáp án
Đáp án là A
Câu 4:
Cho đường tròn (O; 5cm). Trên đường tròn này lấy dây AB bằng 6 cm. Khoảng cách từ tâm O đến dây AB là:
Xem đáp án
Đáp án là C
Câu 5:
Một dây AB của đường tròn tâm (O) có độ dài 12 cm. Biết khoảng cách từ tâm O đến dây là 8 cm. Bán kính của đường tròn đó bằng:
Xem đáp án
Đáp án là B
Câu 6:
Biết đường kính của một đường tròn là 10cm. Biết khoảng cách từ tâm O của đường tròn đến đường thẳng a là 5 cm. Vị trí tương đối của đường thẳng và đường tròn là:
Xem đáp án
Đáp án là B
Câu 7:
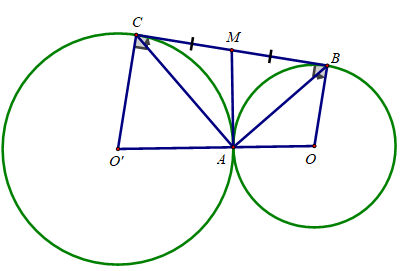
Cho hai đường tròn (O;R) và (O;r) tiếp xúc ngoài tại A. Một đường thẳng (d) tiếp xúc với cả hai đường tròn trên tại B và C với B ∈ (O), C ∈ (O’).
a) Chứng minh tam giác ABC vuông
Xem đáp án
a) Ta có:
OB // O'C ( cùng vuông góc với d)
⇒ Tứ giác OBCO' là hình thang vuông
⇒ ∠(BOO') + ∠(CO'O) =
Δ CO'A cân tại O' có:
Từ (1) và (2):
Lại có: ∠(CAO') + ∠(BAO) + ∠(BAC) = ⇒ ∠(BAC) = - =
⇒ ΔABC vuông tại A.
Câu 8:
Cho hai đường tròn (O;R) và (O;r) tiếp xúc ngoài tại A. Một đường thẳng (d) tiếp xúc với cả hai đường tròn trên tại B và C với B ∈ (O), C ∈ (O’).
b) Gọi M là trung điểm của BC. Chứng minh MA là tiếp tuyến chung của hai đường tròn (O) và (O‘).
Xem đáp án
b) Ta có: M là trung điểm của cạnh huyền BC
⇒ MA = MB = MC
⇒ ΔMAB cân tại M ⇒ ∠(MAB ) = ∠(MBA )
Lại có: ΔOAB cân tại O ⇒ ∠(OAB ) = ∠(OBA )
⇒ ∠(MAB ) + ∠(OAB ) = ∠(MBA ) + ∠(OBA ) ⇔ ∠(MAO ) = ∠(MBO) =
⇒ MA là tiếp tuyến của (O)
Chứng minh tương tự: MA là tiếp tuyến của (O')
Vậy MA là tiếp tuyến chung của hai đường tròn (O) và (O')
Câu 9:
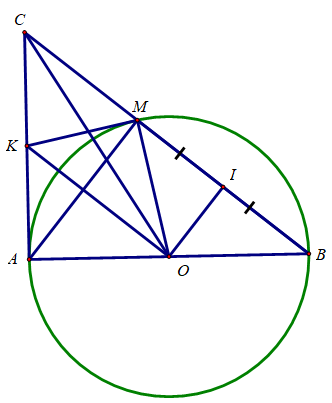
Cho đường tròn (O) đường kính AB. Trên tiếp tuyến Ax lấy điểm C ≠A . Đoạn thẳng BC cắt (O) tại M. Gọi I là trung điểm của MB, K là trung điểm của AC
Xem đáp án
a) Tam giác AMB nội tiếp đường tròn (O) có AB là đường kính
⇒ ΔAMB vuông tại M hay ∠(AMB) = 90o
⇒ AM là đường cao của tam giác ABC
Xét tam giác ABC vuông tại A có AM là đường cao
⇒ = CM.CB (hệ thức liên hệ giữa cạnh và đường cao)
Câu 10:
Cho đường tròn (O) đường kính AB. Trên tiếp tuyến Ax lấy điểm C ≠A . Đoạn thẳng BC cắt (O) tại M. Gọi I là trung điểm của MB, K là trung điểm của AC
b) Chứng minh A, I, C, M cùng nằm trên 1 đường tròn
Xem đáp án
b) Tam giác ACO vuông tại A ⇒ Tâm đường tròn ngoại tiếp tam giác ACO là trung điểm của CO (1)
Xét tam giác AMB có:
I là trung điểm của AM
O là trung điểm của AB
⇒ IO là đường trung bình của tam giác AMB
⇒ IO // AM
Mà AM ⊥ MB ⇒ IO ⊥ MB
Tam giác CIO vuông tại I ⇒ Tâm đường tròn ngoại tiếp tam giác CIO là trung điểm của CO (2)
Từ (1) và (2) ⇒ 4 điểm A, I, C, O cùng thuộc một đường tròn
Câu 11:
Cho đường tròn (O) đường kính AB. Trên tiếp tuyến Ax lấy điểm C ≠A . Đoạn thẳng BC cắt (O) tại M. Gọi I là trung điểm của MB, K là trung điểm của AC
c) Chứng minh KM là tiếp tuyến của đường tròn (O)
Xem đáp án
c) Tam giác CMA vuông tại M có MK là trung tuyến
⇒ MK = KA = KC
Xét Δ KAO và Δ KMO có:
KA = KM
KO là cạnh chung
AO = MO ( = bán kính (O))
⇒ Δ KAO = Δ KMO (c.c.c)
⇒ ∠(KAO) = ∠(KMO)
Mà ∠(KAO) = ⇒ ∠(KMO) =
⇒ KM là tiếp tuyến của (O)