9 câu hỏi trắc nghiệm thuộc Góc ở tâm. Số đo cung có đáp án (Thông hiểu)

Góc ở tâm. Số đo cung có đáp án (Thông hiểu)

Đề số 1

Góc ở tâm. Số đo cung có đáp án (Thông hiểu)

521 lượt thi
9 câu hỏi
30 phút

Danh sách câu hỏi

Câu 1:

Cho hai tiếp tuyến tại C và D của đường tròn (O) cắt nhau tại N, biết $\hat{C N D}$ = 60^o. Số đo cung CD nhỏ và số đo cung CD lớn lần lượt là:

A. 150^o; 210^o

B. 120^o; 230^o

C. 120^o; 240^o

D. 240^o; 120^o

Xem đáp án

Xét tứ giác ODNC có $\hat{C O D} + \hat{O C N} + \hat{C N D} + \hat{O D N}$ = 360^o

$\hat{C O D}$ = 360^o − $\hat{O C N} - \hat{O D N} - \hat{C N D}$ = 360^o – 90^o – 90^o – 60^o = 120^o

Suy ra số đo cung nhỏ CD là 120^o; số đo cung lớn CD là 360^o – 120^o = 240^o

Đáp án cần chọn là: C

Câu 2:

Cho tam giác ABC đều nội tiếp đường tròn (O). Tính số đo cung AC lớn

A. 240^o

B. 120^o

C. 360^o

D. 210^o

Xem đáp án

Vì tam giác ABC đều có O là tâm đường tròn ngoại tiếp nên O cũng là giao ba đường phân giác nên AO; CO lần lượt là các đường phân giác $\hat{B A C}$ ;

Ta có $\hat{C A O} = \frac{1}{2} \hat{B A C} = \frac{60^{o}}{2}$ = 30^o;

$\hat{A C O} = \frac{1}{2} \hat{A C B} = \frac{60^{o}}{2} = 30^{o}$

Xét tam giác AOC có $\hat{A O C}$ = 180^o − $\hat{C A O} - \hat{A C O}$ = 120^o nên số đo cung nhỏ AC là 120^o

Do đó số đo cung lớn AC là 360^o – 120^o = 240^o

Đáp án cần chọn là: A

Câu 3:

Cho tam giác ABC đều nội tiếp đường tròn (O). Tính số đo cung BC nhỏ

A. 240^o

B. 60^o

C. 180^o

D. 120^o

Xem đáp án

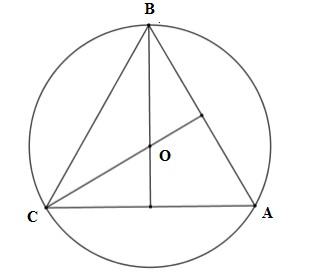
Vì tam giác ABC đều có O là tâm đường tròn ngoại tiếp nên O cũng là giao ba đường phân giác nên BO; CO lần lượt là các đường phân giác $\hat{A B C}; \hat{A C B}$

Ta có $\hat{B C O} = \frac{1}{2} \hat{A C B} = \frac{60^{o}}{2} = 30^{o}; \hat{C B O} = \frac{1}{2} \hat{A B C} = \frac{60^{o}}{2} = 30^{o}$

Xét tam giác BOC có

$\hat{B O C} = 180^{o} - \hat{C B O} - \hat{B C O}$ = 180^o – 30^o – 30^o = 120^o

Do đó số đo cung nhỏ BC là 120^o

Đáp án cần chọn là: D

Câu 4:

Cho đường tròn (O; R), lấy điểm M nằm ngoài (O) sao cho OM = 2R. Từ M kẻ tiếp tuyến MA và MB với (O) (A, B là các tiếp điểm). Số đo góc $\hat{A O M}$ là:

A. 30^o

B. 120^o

C. 50^o

D. 60^o

Xem đáp án

Xét tam giác AOM vuông tại A ta có:

cos $\hat{A O M}$ = $\frac{O A}{O M} = \frac{R}{2 R} = \frac{1}{2} \Rightarrow \hat{A O M} = 60^{o}$

Đáp án cần chọn là: D

Câu 5:

Cho đường tròn (O; R), lấy điểm M nằm ngoài (O) sao cho OM = 2R. Từ M kẻ tiếp tuyến MA và MB với (O) (A, B là các tiếp điểm). Số đo cung AB nhỏ là:

A. 240^o

B. 120^o

C. 360^o

D. 210^o

Xem đáp án

Xét đường tròn (O) có MA; MB là hai tiếp tuyến cắt nhau tại M nên OM là tia phân giác của góc $\hat{A O B}$

Suy ra $\hat{A O B} = 2 \hat{A O M}$ = 2. 60^o = 120^o mà $\hat{A O B}$ là góc ở tâm chắn cung AB

Nên số đo cung nhỏ AB là 120^o

Đáp án cần chọn là: B

Câu 6:

Cho đường tròn (O; R), lấy điểm M nằm ngoài (O) sao cho OM = $\sqrt{2}$ R. Từ M kẻ tiếp tuyến MA và MB với (O) (A, B là các tiếp điểm). Số đo góc là:

A. 45^o

B. 30^o

C. 90^o

D. 60^o

Xem đáp án

Xét tam giác AOB vuông tại A ta có:

sin $\hat{B M O}$ = $\frac{O B}{O M} = \frac{R}{\sqrt{2} R} = \frac{1}{\sqrt{2}} \Rightarrow \hat{B M O} = 45^{o}$

Đáp án cần chọn là: A

Câu 7:

Cho (O; R) và dây cung MN = R $\sqrt{2}$ . Kẻ OI vuông góc với MN tại I. Tính độ dài OI theo R.

A. $\frac{R \sqrt{3}}{3}$

B. $\frac{R}{\sqrt{2}}$

C. $\frac{R}{3}$

D. $\frac{R}{2}$

Xem đáp án

Xét (O) có OI $⊥$ MN tại I nên I là trung điểm của MN

$\Rightarrow$ MI = IN = $\frac{\sqrt{2} R}{2}$

Xét tam giác OIM vuông tại I, theo định lý Pytago ta có:

OI² = OM² – MI²

=> OI = $\sqrt{R^{2} - {(\frac{\sqrt{2} R}{2})}^{2}} = \frac{\sqrt{2} R}{2}$

Đáp án cần chọn là: B

Câu 8:

Cho đường tròn (O) đường kính AB, vẽ góc ở tâm $\hat{A O C}$ = 55^o. Vẽ dây CD vuông góc với AB và dây DE song song với AB. Tính số đo cung nhỏ BE

A. 55^o

B. 60^o

C. 40^o

D. 50^o

Xem đáp án

Xét (O) có CD $⊥$ OA; ED // OA => CD $⊥$ ED hay $\hat{E D C}$ = 90^o

mà E; D; C $\in$ (O) nên EC là đường kính của (O) hay E; O; C thẳng hàng

Do đó $\hat{B O E} = \hat{C O A}$ = 55^o (đối đỉnh) nên số đo cung nhỏ BE là 55^o

Đáp án cần chọn là: A

Câu 9:

Cho đường tròn (O) đường kính AB, vẽ góc ở tâm $\hat{A O C}$ = 60^o. Vẽ dây CD vuông góc với AB và dây DE song song với AB. Tính số đo cung nhỏ BE

A. 120^o

B. 60^o

C. 240^o

D. 30^o

Xem đáp án

Xét (O) có CD $⊥$ OA; ED // OA => CD $⊥$ ED hay $\hat{E D C}$ = 90^o

mà E; D; C (O) nên EC là đường kính của (O) hay E; O; C thẳng hàng

Do đó $\hat{B O E} = \hat{C O A}$ = 60^o (đối đỉnh) nên số đo cung nhỏ BE là 60^o

Đáp án cần chọn là: B

Bắt đầu thi ngay

CHỌN BỘ SÁCH BẠN MUỐN XEM

Góc ở tâm. Số đo cung có đáp án (Thông hiểu)

Góc ở tâm. Số đo cung có đáp án (Thông hiểu)

Danh sách câu hỏi

Có thể bạn quan tâm

Các bài thi hot trong chương