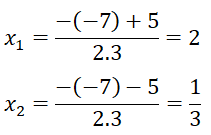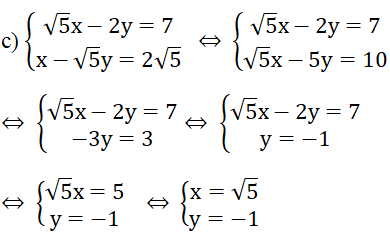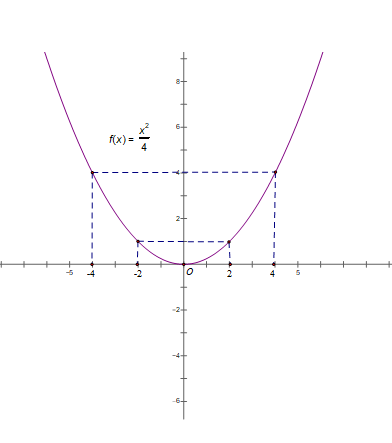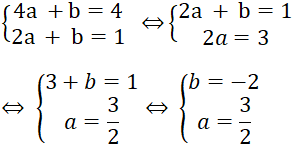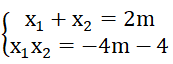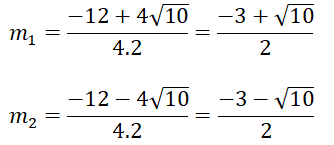12 câu hỏi trắc nghiệm thuộc Đề thi Học kì 2 Toán 9 chọn lọc, có đáp án

Câu 1:

Giải các phương trình và hệ phương trình sau:

a) 3 $x^{2}$ – 7x + 2 = 0

Xem đáp án

a) 3 $x^{2}$ – 7x + 2 = 0

Δ= $7^{2}$ -4.3.2 = 49 - 24 = 25 > 0 ⇒ $\sqrt{∆}$ = 5

Phương trình có 2 nghiệm phân biệt:

Vậy tập nghiệm của phương trình là S = {2; 1/3}

Câu 2:

Giải các phương trình và hệ phương trình sau:

b) $x^{4}$ – 5x + 4 = 0

Xem đáp án

b) $x^{4} - 5 x^{2}$ + 4 = 0

Đặt t = $x^{2}$ ≥ 0 , ta có phương trình:

$t^{2}$ - 5t + 4 = 0 (dạng a + b + c = 1 -5 + 4 = 0)

$t_{1}$ = 1 (nhận) ; $t_{2}$ = 4 (nhận)

với t = 1 ⇔ $x^{2}$ = 1 ⇔ x = ± 1

với t = 4 ⇔ $x^{2}$ = 4 ⇔ x = ± 2

Vậy nghiệm của phương trình x = ±1; x = ± 2

Câu 3:

Giải các phương trình và hệ phương trình sau:

c) $\{\begin{cases} \sqrt{5} x - 2 y = 7 \\ x - \sqrt{5} y = 2 \sqrt{5} \end{cases}$

Xem đáp án

Vậy hệ phương trình có nghiệm (x; y) = ( $\sqrt{5}$ ; -1)

Câu 4:

a) Vẽ đồ thị (P) hàm số y= $x^{2}$ /4

Xem đáp án

a) Tập xác định của hàm số: R

Bảng giá trị:

x	-4	-2	0	2	4
y = $x^{2}$ / 4	4	1	0	1	4

Đồ thị hàm số y = $x^{2}$ /4 là một đường parabol nằm phía trên trục hoành, nhận trục Oy làm trục đối xứng và điểm O(0;0) là đỉnh và là điểm thấp nhất.

Câu 5:

b) Trên (P) lấy 2 điểm A và B có hoành độ lần lượt là 4 và 2. Viết phương trình đường thẳng đi qua A và B

Xem đáp án

b) Với x = 4, ta có: y = $x^{2}$ /4 = 4 ⇒ A (4; 4)

Với x = 2, ta có y = $x^{2}$ /4 = 1 ⇒ B ( 2; 1)

Giả sử đường thẳng đi qua 2 điểm A, B là y = ax + b

Đường thẳng đi qua A (4; 4) nên 4 = 4a + b

Đường thẳng đi qua B (2; 1) nên : 1= 2a + b

Ta có hệ phương trình

Vậy phương trình đường thẳng đi qua 2 điểm A, B là y = 3/2 x - 2

Câu 6:

Cho phương trình (ẩn x) : $x^{2}$ – 2mx – 4m – 4 = 0(1)

a) Chứng tỏ phương trình (1) có nghiệm với mọi Giá trị của m.

Xem đáp án

a) Δ' = $m^{2}$ - (-4m - 4) = $m^{2}$ + 4m + 4 = ${(m + 2)}^{2}$ ≥ 0 ∀m

Vậy phương trình đã cho luôn có nghiệm với mọi m

Câu 7:

Cho phương trình (ẩn x) : $x^{2}$ – 2mx – 4m – 4 = 0(1)

b) Tìm m để phương trình (1) có 2 nghiệm $x_{1}, x_{2}$ thỏa mãn ${x_{1}}^{2} + {x_{2}}^{2} - x_{1} x_{2} = 13$ = 13

Xem đáp án

b) Gọi $x_{1}$ ; $x_{2}$ lần lượt là 2 nghiệm của phương trình đã cho

Theo hệ thức Vi-et ta có:

${x_{1}}^{2} + {x_{2}}^{2}$ - $x_{1}$ $x_{2}$ = ${(x_{1} + x_{2})}^{2}$ - 3x1 x2 = 4 $m^{2}$ + 3(4m + 4)

Theo bài ra: ${x_{1}}^{2} + {x_{2}}^{2}$ - $x_{1}$ $x_{2}$ =13

⇒ 4m2 + 3(4m + 4) = 13 ⇔ 4m2 + 12m - 1 = 0

$∆_{m}$ = 122 -4.4.(-1) = 160 ⇒ $\sqrt{∆_{m}} = 4 \sqrt{10}$

Phương trình có 2 nghiệm phân biệt

Vậy với 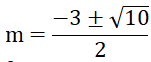thì phương trình có 2 nghiệm $x_{1}$ ; $x_{2}$ thỏa mãn điều kiện ${x_{1}}^{2} + {x_{2}}^{2}$ - $x_{1}$ $x_{2}$ = 13

Câu 8:

Tìm kích thước của hình chữ nhật, biết chiều dài hơn chiều rộng 3m. Nếu tăng thêm mỗi chiều thêm 2 mét thì diện tích của hình chữ nhật tăng thêm 70 $m^{2}$ .

Xem đáp án

Gọi chiều rộng của hình chữ nhật là x (m) ( x > 0 )

⇒ Chiều dài của hình chữ nhật là x + 3 (m)

Khi đó diện tích của hình chữ nhật là x(x + 3) ( $m^{2}$ )

Nếu tăng thêm mỗi chiều thêm 2 mét thì diện tích của hình chữ nhật tăng thêm 70 $m^{2}$ nên ta có phương trình:

(x + 2)(x + 3 + 2) = x(x + 3) + 70

⇔ (x + 2)(x + 5) = x(x + 3) + 70

⇔ $x^{2}$ + 7x + 10 = $x^{2}$ + 3x + 70

⇔ 4x = 60

⇔ x = 15

Vậy chiều rộng của hình chữ nhật là 15m

Chiều dài của hình chữ nhật là 18m