Đề kiểm tra giữa kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề số 7
-
3250 lượt thi
-
5 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Cho biểu thức:
A = + và B = với x ≠ ± 3
a) Tính giá trị của biểu thức A khi x = −1.
b) Rút gọn biểu thức P = A : B.
c) Tìm x Î ℤ để P có giá trị là số nguyên.
Xem đáp án
a) Khi x = −1 (TMĐK), giá trị của biểu thức A bằng:
A = = = .
Vậy khi x = −1 giá trị của biểu thức A bằng .
b) Ta có: A = +
= += .
P = =
= . =
c) Ta có: P = = = 1 −
Để P có giá trị nguyên thì giá trị của cũng phải nguyên.
Do đó (x + 3) Î Ư(2) = {±1; ±2}.
Ta có bảng sau:
Câu 2:
Giải các phương trình sau:
a) x(x − 1) − (x2 − 3x + 5) = 0.
b) (x − 5)2 + 6x − 30 = 0.
c) − = . Xem đáp án
a) x(x − 1) − (x2 − 3x + 5) = 0
Û x2 − x − x2 + 3x − 5 = 0
Û 2x − 5 = 0
Û x =
Vậy tập nghiệm của phương trình là .
b) (x − 5)2 + 6x − 30 = 0
Û (x − 5)2 + 6(x – 5) = 0
Û (x – 5). [(x – 5) + 6] = 0
Û (x – 5). (x + 1) = 0
Û
Û
Vậy tập nghiệm của phương trình là S = {5; −1}.
c)
ĐKXĐ:
Phương trình đã cho tương đương với:
Þ x2 – (x – 2) = 2
Û x2 − x + 2 − 2 = 0
Û x2 − x = 0
Û x(x – 1) = 0
Vậy tập nghiệm của phương trình là S = {1}.
Câu 3:
Xem đáp án
Gọi x (km) là độ dài quãng đường AB (x > 0)
Xe ô tô đi từ A đến B với vận tốc 50 km/h nên thời gian ô tô chở hàng đi từ A đến B là:
(giờ).
Ô tô đi từ B về A với vận tốc 60 km/h nên thời gian ô tô chở hàng đi từ B đến A là:
(giờ)
Đổi 30 phút = giờ.
Vì tổng thời gian ô tô đi, thời gian về và nghỉ là 6 giờ nên ta có phương trình:
+ + = 6
Û
Û
Û x = 150 (thỏa mãn)
Vậy độ dài quãng đường AB là 150 km.Câu 4:
Cho tam giác ABC vuông tại A. Qua A kẻ đường cao AH (H Î BC).
a) Chứng minh tam giác ABC đồng dạng với tam giác HAC.
b) Khi cho AB = 6cm; AC = 8cm, tính độ dài đoạn BC và AH.
c) Từ H kẻ HE vuông góc với AC tại E. Chứng minh HE2 = AE. EC.
d) Gọi I là trung điểm của AH, EI cắt AB tại F. Chứng minh AH2 = FA. FB + EA. EC. Xem đáp án
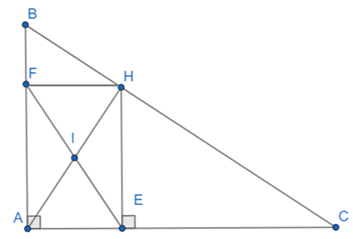
a) Vì tam giác ABC vuông tại A nên
Theo đề bài, AH là đường cao của tam giác ABC nên AH ^ BC hay = 90°
Do đó = 90°.
Xét ∆ABC và ∆HAC có:
= 90° (chứng minh trên)
chung
Do đó ∆ABC ∆HAC (g.g)b) Áp dụng định lý Py-ta-go vào ∆ABC vuông tại A, ta có:
BC2 = AB2 + AC2 = 62 + 82 = 100
Suy ra BC = 10 cm.
Tam giác ABC có AH là đường cao tương ứng với cạnh đáy BC nên:
SABC = .AH. BC (1)
Mặt khác, tam giác ABC vuông tại A nên:
SABC = .AB.AC (2)
Từ (1) và (2) suy ra SABC = .AB.AC = .AH. BC
Do đó AH = = = 4,8 (cm).
Vậy BC = 10 cm; AH = 4,8 cm.c) Ta có: + = 90° và + = 90°
Suy ra =
Xét ∆AEH và ∆CHE có:
(chứng minh trên)
= 90° (HE ^ AC tại E)
Do đó ∆AEH ∆CHE (g.g)
Suy ra (các cạnh tương ứng)
Do đó HE2 = AE. EC (đpcm) (1)d) Ta có: AB ⊥ AC (vì ∆ABC vuông tại A) và HE ⊥ AC (giả thiết)
Suy ra AB // HE.
Do đó = (hai góc so le trong)
Xét ∆AIF và ∆EIH có:
= (chứng minh trên)
IA = IH (giả thiết)
= (hai góc đối đỉnh)
Do đó ∆AIF = ∆EIH (g.c.g)
Suy ra AF = HE (hai cạnh tương ứng)
Mà AF // HE (vì HE // AB)
Do đó AEHF là hình bình hành.
Mặt khác, = 90°
Do đó AEHF là hình chữ nhật
Suy ra = 90°.
Do đó = = 90°.
Mặt khác, ABCD là hình chữ nhật nên hai đường chéo AH và EF bằng nhau; AH cắt EF tại trung điểm I.
Suy ra IH = IF nên ∆HIF cân tại I.
Do đó .
Xét ∆AFH và ∆EHF có:
(chứng minh trên)
= = 90° (chứng minh trên)
Do đó ∆AFH ∆EHF (g.g).
Suy ra (các cặp cạnh tương ứng)
Nên FA . FB = HF2 (2)
Từ (1) và (2) suy ra AF. FB + AE. EC = HF2 + HE2
Xét ∆FHE vuông góc tại H có:
HF2 + HE2 = EF2 = AH2 (vì EF = AH)
Do đó AH2 = FA. FB + EA. EC (đpcm).Câu 5:
Cho (a + b + c)2 = a2 + b2 + c2 và a, b, c khác 0.
Chứng minh rằng: + + = . Xem đáp án
Ta có: (a + b + c)2 = a2 + b2 + c2
ab + bc + ca = 0
Mà a, b, c khác 0 nên + + = 0
(đpcm).