Bài 2. Hai đường thẳng cắt nhau. Hai đường thẳng song song
-
321 lượt thi
-
11 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
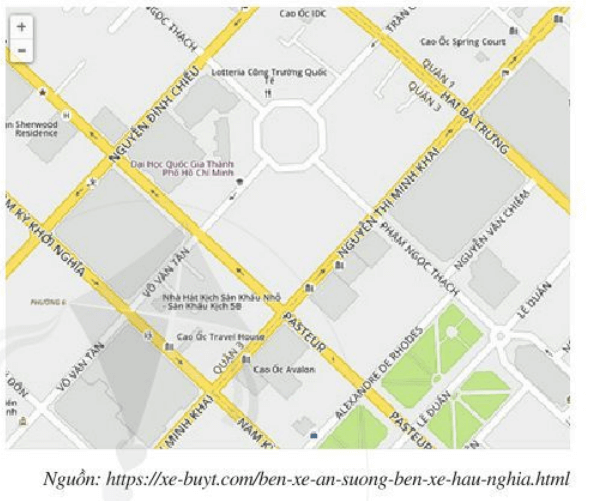
Quan sát một phần bản đồ giao thông ở TP. Hồ Chí Minh và đọc tên một số đường phố.
Hai đường phố nào gợi nên hình ảnh hai đường thẳng song song? Hai đường thẳng cắt nhau?
Xem đáp án
Một số đường phố xuất hiện ở bản đồ trên là:
Nguyễn Đình Chiểu, Nguyễn Thị Minh Khai, Pasteur, Tam Kỳ khởi nghĩa, Lê Duẩn, Phạm Ngọc Thạch, Hai Bà Trưng, Alexandre de Rhodes, Võ Văn Tần, …
Qua tìm hiểu bài học này chúng ta biết được:
Hai đường thẳng song song là hai đường thẳng không có điểm chung.
Hai đường thẳng cắt nhau là hai đường thẳng có một điểm chung.
Do đó, ta có:
Hai đường phố gợi lên hình ảnh hai đường thẳng song song là: Nguyễn Đình Chiểu và Nguyễn Thị Minh Khai.
Hai đường phố gợi lên hình ảnh hai đường thẳng cắt nhau là: Nguyễn Đình Chiểu và Tam Kỳ khởi nghĩa.
Câu 2:
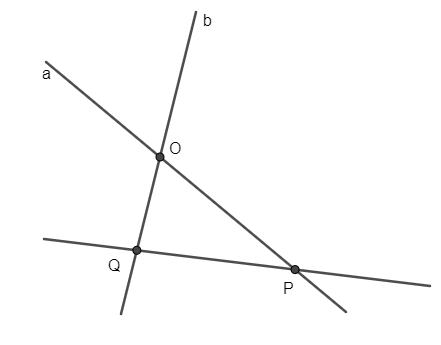
Hai đường thẳng ở Hình 26 có bao nhiêu điểm chung?
Xem đáp án
Hai đường thẳng ở Hình 26 có 1 điểm chung duy nhất là O.
Câu 3:
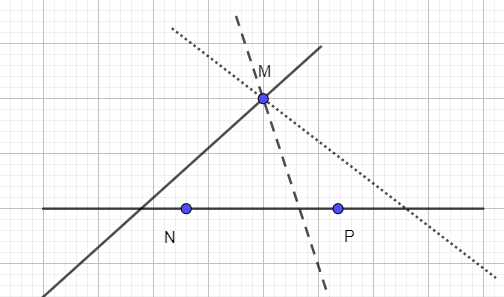
Cho ba điểm M, N, P như Hình 30.
a) Vẽ đường thẳng NP.
b) Vẽ hai đường thẳng đi qua M và cắt đường thẳng NP.
Xem đáp án
a) Đường thẳng NP:
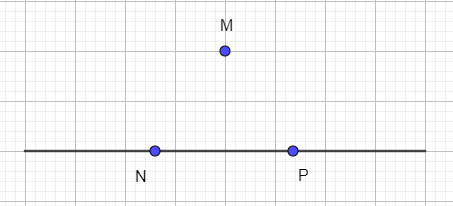
b) Ta có thể vẽ được vô số đường thẳng qua M cắt đường thẳng NP:
Câu 4:
Mỗi bức ảnh sau đây gợi nên hình ảnh về hai đường thẳng. Hai đường thẳng đó có điểm chung không?
Xem đáp án
Hình ảnh các con đường nhìn từ trên cao là các đường thẳng không có điểm chung.
Hình ảnh hai đường dây điện trên bầu trời là các đường thẳng không có điểm chung.
Câu 5:
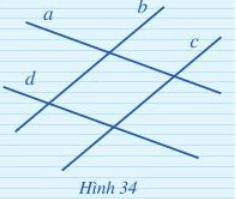
Quan sát Hình 34
a) Chỉ ra các cặp đường thẳng song song.
b) Chỉ ra các cặp đường thẳng cắt nhau.
Xem đáp án
a) Các cặp đường thẳng song song là: a và d, b và c.
b) Các cặp đường thẳng cắt nhau là: a và b, a và c, b và d, c và d.
Câu 6:
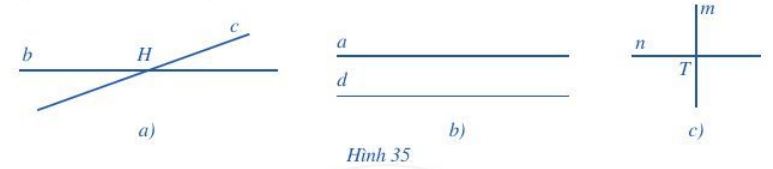
Quan sát Hình 35, đọc tên hai đường thẳng song song, hai đường thẳng cắt nhau và chỉ ra giao điểm của chúng (nếu có).
Xem đáp án
Hai đường thẳng song song là a và b.
Hai đường thẳng cắt nhau là m và n với giao điểm là T.
Hai đường thẳng cắt nhau là b và c với giao điểm là H.
Câu 7:
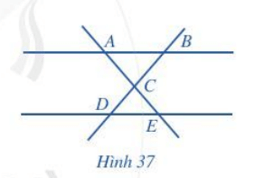
Quan sát Hình 36 và chỉ ra:
a) Các cặp đường thẳng song song.
b) Các cặp đường thẳng cắt nhau.
Xem đáp án
a) Các cặp đường thẳng song song:
a và b, b và c, a và c, d và e.
b) Các cặp đường thẳng cắt nhau:
a và d, a và e, b và d, b và e, c và d, c và e.
Câu 8:
Chỉ ra các đường thẳng cắt nhau:
Xem đáp án
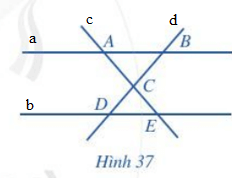
Các đường thẳng cắt nhau:
Đường thẳng a và đường thẳng c với giao điểm là A;
Đường thẳng a và đường thẳng d với giao điểm là B;
Đường thẳng b và đường thẳng d với giao điểm là D;
Đường thẳng b và đường thẳng c với giao điểm là E;
Đường thẳng c và đường thẳng d với giao điểm là C.
Câu 9:
Cho ba điểm H, I, K thẳng hàng.
a) Điểm K có thuộc đường thẳng IH không?
b) Vẽ đường thẳng d đi qua H và không đi qua I. Đường thẳng d có song song với đường thẳng IK không?
Xem đáp án
a) Qua hai điểm I và H ta chỉ vẽ được duy nhất một đường thẳng đi qua hai điểm này.
Mà ba điểm H, I, K thẳng hàng nên K phải thuộc đường thẳng IH.
Vậy điểm K thuộc đường thẳng IH.
b) Vì ba điểm H, I, K thẳng hàng nên đường thẳng IK đi qua điểm H, mà đường thẳng d cũng đi qua điểm H nên hai đường thẳng này có điểm chung là H. Do đó đường thẳng d không song song với đường thẳng IK.
Câu 10:
Cho ba điểm P, Q, R không thẳng hàng. Vẽ các đường thẳng đi qua hai trong ba điểm đã cho.
a) Điểm P là giao điểm của hai đường thẳng nào?
b) Chỉ ra các cặp đường thẳng cắt nhau.
Xem đáp án
a) Ta vẽ đường thẳng a đi qua hai điểm P và Q; đường thẳng b đi qua hai điểm Q và R, đường thẳng c đi qua hai điểm P và R.
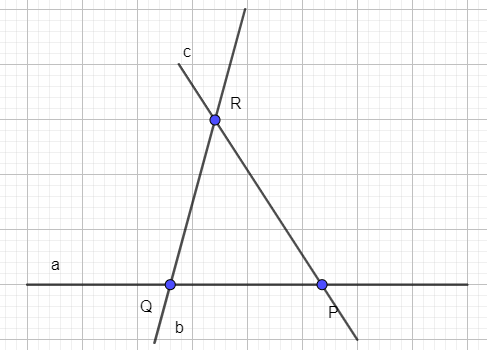
Ta thấy điểm P là giao điểm của hai đường thẳng a và c.
b) Các cặp đường thẳng cắt nhau là:
Đường thẳng a và đường thẳng b với giao điểm là Q;
Đường thẳng a và đường thẳng c với giao điểm là P;
Đường thẳng b và đường thẳng c với giao điểm là R.
Câu 11:
Vẽ hình theo cách diễn đạt sau:
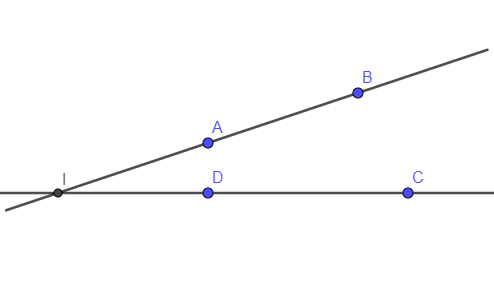
a) Đường thẳng AB và đường thẳng CD cắt nhau tại I.
b) Hai đường thẳng a và b cắt nhau tại O, đường thẳng c cắt a tại P và cắt b tại Q.
Xem đáp án
a) – Chấm bốn điểm A, B, C và D (sao cho 4 điểm này không cùng nằm trên một đường thẳng)
- Ta vẽ đường thẳng AB đi qua hai điểm A và B, vẽ đường thẳng CD đi qua hai điểm C và D. Hai đường thẳng này cắt nhau tại I.
b) - Vẽ hai đường thẳng a và b bất kì cắt nhau tại O.
- Vẽ đường thẳng c cắt a tại P và cắt b tại Q
