Trong một hộp kín có 6 tấm thẻ ghi các chữ K, H, O, A, N, H. Lấy ngẫu nhiên ra một tấm thẻ. Hỏi có bao nhiêu kết quả có thể xảy ra đối với tấm thẻ được lấy ra?

A. 3;

B. 4;

C. 5;

D. 6.

Trong danh sách ghi trong sổ điểm, mỗi bạn lớp 6A đều có một số thứ tự. Chọn ngẫu nhiên một bạn trong lớp 6A. Số thứ tự của bạn được chọn đó

A. có thể chia hết cho 5.

B. có thể là số 92.

C. chắc chắn là số chẵn.

D. có chữ số hàng trăm bằng 1.

Quay đồng thời hai vòng quay như hình bên. Quan sát khi các vòng quay dừng lại, hai mũi tên chỉ vào các ô ghi số nào rồi tính tổng của hai số đó.

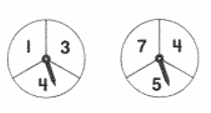
Tổng lớn nhất có thể nhận được bằng:

A. 8;

B. 9;

C. 10;

D. 11.

Quay đồng thời hai vòng quay như hình bên. Quan sát khi các vòng quay dừng lại, hai mũi tên chỉ vào các ô ghi số nào rồi tính tổng của hai số đó.

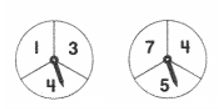
Tổng trên có bao nhiêu các kết quả có thể?

A. 5;

B. 6;

C. 7;

D. 8.

Quay đồng thời hai vòng quay như hình bên. Quan sát khi các vòng quay dừng lại, hai mũi tên chỉ vào các ô ghi số nào rồi tính tổng của hai số đó.

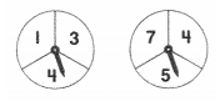
Sự kiện tổng hai số bằng 12 có xảy ra hay không?

A. Chắc chắn.

B. Không thể.

C. Có thể.

D. Không có thông tin.

Một đề thi trắc nghiệm có 30 câu. Một học sinh làm bài bằng cách khoanh ngẫu nhiên các đáp án ở mỗi câu. Khi trả bài bạn đó thấy có 18 câu sai. Xác suất thực nghiệm của sự kiện Khoanh được đáp án đúng bằng:

A. $\frac{1}{30}$ ;

B. $\frac{1}{4}$ ;

C. $\frac{2}{5}$ ;

D. $\frac{3}{5}$ .

Viết tiếp “không thể”, “có thể” hoặc “chắc chắn” vào chỗ chấm cho thích hợp với mỗi sự kiện sau:

a) Trong một trận thi đấu bóng chuyền, ……….. sẽ có đội thắng

b) Bạn học sinh mới chuyển tới lớp 6A ………. là người học giỏi Toán.

c) Ta .......... chọn được quả bóng xanh từ một hộp chỉ có toàn bóng đỏ.

Trong hộp có 4 tấm thẻ ghi các số như hình bên.

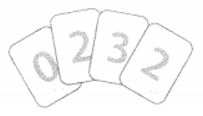
Không nhìn vào hộp, rút ngẫu nhiên ra một tấm thẻ và nhớ số ghi trên thẻ. Trả lại thẻ vào hộp rồi lại rút tiếp ra một tấm thẻ. Tính tổng các số ghi trên hai tấm thẻ ở hai lần rút.

a) Viết tập hợp các kết quả có thể xảy ra đối với tổng các số ghi trên hai thẻ đã rút ra.

b) Viết tập hợp các kết quả có thể để sự kiện Tổng các số ghi trên hai thẻ rút ra không là số lẻ xảy ra.

c) Sự kiện Tổng các số ghi trên hai thẻ rút ra bằng 6 có xảy ra không? Tại sao?

Một cầu thủ bóng đá tập sút 20 quả penalty, kết quả được ghi chép lại như sau:

x; o; x; o; o; x; x; x; o; x; x; x; o; o; x; x; x; x; o; x

ở đó x là kí hiệu sút thành công còn o là kí hiệu sút hỏng.

a) Lập bảng thống kê dữ liệu trên.

b) Tính xác suất thực nghiệm của các sự kiện sút vào và sút hỏng.

Phỏng vấn 200 người về chương trình họ yêu thích nhất trên truyền hình, số liệu trong bảng thống kê sau:

Tính xác suất thực nghiệm xuất hiện:

a) người yêu thích chương trình Thể thao.

b) người yêu thích chương trình Ca nhạc hoặc Giải trí.

c) người không yêu thích chương trình Giải trí.

Biểu đồ tranh dưới đây cho dữ liệu trong ngày về số khách lựa chọn mua các loại Hồng trà, Trà sữa Matcha và Trà sữa khoai môn tại một cửa hàng.

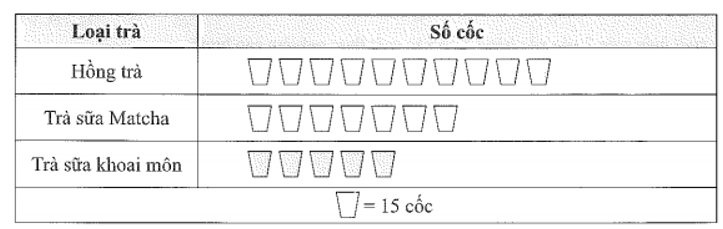
a) Tính xác suất thực nghiệm xuất hiện khách mua Hồng trà.

b) Tính xác suất thực nghiệm xuất hiện khách không mua Trà sữa Matcha.

c) Có một khách mới vào cửa hàng. Nếu cần dự đoán trước, em có thể đoán được người đó nhiều khả năng sẽ mua loại trà nào không?

Một cửa hàng sau khi thay đổi mẫu để ra một sản phẩm bánh mới đã thăm dò ý kiến khách hàng. Kết quả nhận được gồm: 40 người thích loại mới hơn loại cũ; 92 người thích loại cũ hơn; 68 người cho rằng không có sự khác biệt. Tính xác suất thực nghiệm của các sự kiện sau:

a) Ý kiến của người thăm dò thích loại bánh mới hơn.

b) Ý kiến của người thăm dò cho thấy có sự khác biệt giữa loại bánh mới và cũ.

Em hãy thử nghiệm gieo 20 lần hai con xúc xắc.

a) Quan sát và ghi lại kết quả tổng số chấm trên mặt xuất hiện của 2 xúc xắc để hoàn thành bảng thống kê sau: