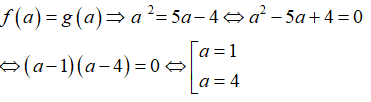Bài 1 (có đáp án): Nhắc lại và bổ sung các khái niệm về hàm số
-
657 lượt thi
-
19 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Cho hàm số y = f(x) xác định trên D . Với , ∈ D; < khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án A
Cho hàm số y = f(x) xác định trên tập D. Khi đó:
• Hàm số đồng biến trên D ⇔ ∀ , ∈ D : < ⇒ f() < f()
• Hàm số nghịch biến trên D ⇔ ∀ , ∈ D : < ⇒ f() > f()
Câu 2:
Cho hàm số f(x) = 3 - . Tính f(-1)
 Xem đáp án
Xem đáp án
Đáp án B
Thay x = -1 vào hàm số ta được: f(x) = 3 - = 2 .
Câu 3:
Cho hàm số f(x) = - 3x - 2. Tính 2.f(3)
 Xem đáp án
Xem đáp án
Đáp án C
Thay X = 3 vào hàm số ta được: f(3) = - 3.3 - 2 = 16 ⇒ 2.f(3) = 2.16 = 32.
Câu 4:
Cho hai hàm số f(x) = -2 và h(x) = 10 - 3x . So sánh f(-2) và h(-1)
 Xem đáp án
Xem đáp án
Đáp án D
Thay x = -2 vào hàm số f(x) = -2 ta được f(-2) = -2.(-8) = 16 .
Thay x = -1 vào hàm số h(x) = 10 - 3x ta được h(-1) = 10 - 3.(-1) = 13.
Nên f(-2) > h(-1) .
Câu 5:
Cho hai hàm số f(x) = và g(x) = 5x - 4 . Có bao nhiêu giá trị của a để f(a) = g(a)
 Xem đáp án
Xem đáp án
Đáp án C
Ta có:
Vậy có 2 giá trị của thỏa mãn.
Câu 6:
Cho hàm số y = 2x + 2. Tìm khẳng định đúng?
 Xem đáp án
Xem đáp án
Đáp án A
Với hai số thực bất kì ; . Giả sử < , suy ra:
2 < 2 ⇒ 2 + 2 < 2 + 2
Hay f() < f()(f() = 2 + 2; f() = 2 + 2)
Do đó, hàm số đã cho đồng biến trên R
Câu 7:
Cho hàm số y = -3x +100. Tìm khẳng định đúng?
 Xem đáp án
Xem đáp án
Đáp án A
Với hai số thực bất kì ; . Giả sử < , suy ra:
-3 > -3 ⇒ -3 + 100 > -3 + 100
Hay f() > f(); (f() = -3 + 100; f() = -3 + 100)
Do đó, hàm số đã cho nghịch biến trên R
Câu 8:
Hàm số xác định với:
 Xem đáp án
Xem đáp án
Đáp án B
Ta có: 0 x + 1 > 0 x
Do đó, hàm số luôn xác định với mọi giá trị của x.
Câu 9:
Cho hàm số y = 2x+ 100 giá trị của y là bao nhiêu khi x=0
 Xem đáp án
Xem đáp án
Đáp án C
Ta có giá trị tương ứng của hàm số khi x= 0 là:
y = f(0) = 2.0 +100 = 100
Câu 10:
Trong các hàm số sau đâu là hàm hằng
 Xem đáp án
Xem đáp án
Đáp án C
Xét hàm số y =2. Với mọi giá trị của x nhưng y luôn nhận giá trị là 2 nên hàm số y =2 là hàm hằng.
Câu 11:
Hàm số là hàm số?
 Xem đáp án
Xem đáp án
TXĐ:
Giả sử
Xét hiệu
Vậylà hàm số đồng biến.
Đáp án cần chọn là: B
Câu 13:
Cho hàm số . Tìm m để hàm số nhận giá trị là −5 khi
 Xem đáp án
Xem đáp án
Thay vào ta được
Đáp án cần chọn là: B
Câu 14:
Cho hàm số 2. Tìm m để đồ thị hàm số đi qua điểm A (2; −3)
 Xem đáp án
Xem đáp án
Thay ta được
Đáp án cần chọn là: C
Câu 15:
Cho hàm số . Tìm m để đồ thị hàm số đi qua điểm A (−3; 6)
 Xem đáp án
Xem đáp án
Thay
Đáp án cần chọn là: D