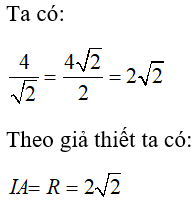Bài 4 (có đáp án): Vị trí tương đối của đường thẳng và đường tròn
-
515 lượt thi
-
10 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Đường thẳng và đường tròn có nhiều nhất bao nhiêu điểm chung
Xem đáp án
Đáp án B
Đường thẳng và đường tròn có nhiều nhất hai điểm chung
Câu 2:
Nếu đường thẳng và đường tròn có duy nhất một điểm chung thì
Xem đáp án
Đáp án A
Đường thẳng và đường tròn chỉ có một điểm chung thì đường thẳng tiếp xúc với đường tròn
Câu 3:
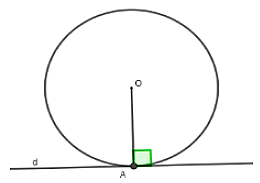
Nếu đường thẳng d là tiếp tuyến của đường tròn (O) tại A thì
Xem đáp án
Đáp án C
Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm
Nên d ⊥ OA tại tiếp điểm A
Câu 4:
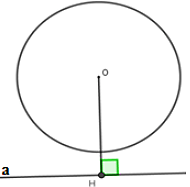
Cho đường tròn (O) và đường thẳng a. Kẻ OH ⊥ a tại H, biết OH > R khi đó đường thẳng a và đường tròn (O)
Xem đáp án
Đáp án B
Vì OH > R nên α không cắt (O)
Câu 5:
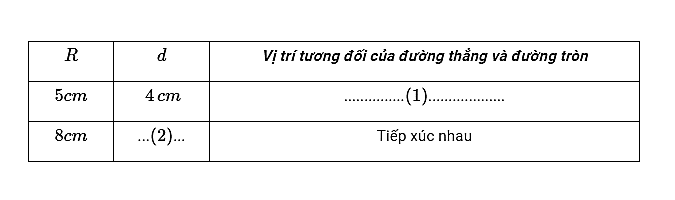
Điền vào các vị trí (1); (2) trong bảng sau (R là bán kính của đường tròn, d là khoảng cách từ tâm đến đường thẳng):
Xem đáp án
Đáp án A
+ Vì d < R (4cm < 5cm) nên đường thẳng cắt đường tròn
+ Vì đường thẳng tiếp xúc với đường tròn nên d = R = 8cm
Câu 6:
Trên mặt phẳng tọa độ Oxy, cho điểm A( 5; 6). Xác định vị trí tương đối của đường tròn (A; 5) với các trục tọa độ?
Xem đáp án
Đáp án A
Ta có khoảng cách từ A đến trục Ox bằng 6 > R.
Đường tròn (A; R) cắt trục Ox tại 2 điểm phân biệt .
Khoảng cách từ A đến trục Oy bằng 5 = R..
Do đó, đường tròn (A; R) tiếp xúc với trục Oy.
Câu 7:
Cho đường tròn tâm (O; 3) và điểm A cách O một khoảng 5 cm. Kẻ tiếp tuyến AB với đường tròn (B là tiếp điểm). Tính AB
Xem đáp án
Đáp án C
Do AB là tiếp tuyến của đường tròn (O) với B là tiếp điểm nên ta có:
⇒
⇒ AB = 4cm
Câu 8:
Cho đường tròn (O; 6cm). Điểm M cách điểm O một khoảng 4cm. Hỏi qua M kẻ được bao nhiêu tiếp tuyến đến đường tròn?
Xem đáp án
Đáp án D
Ta có: OM = 4 cm và R = 6 cm nên OM < R
Do đó, điểm M nằm trong đường tròn (O).
Suy ra, qua điểm M không kẻ được tiếp tuyến nào đến đường tròn
Câu 9:
Cho đường tròn , cho điểm A thỏa mãn: IA = . Hỏi qua điểm A kẻ được bao nhiêu tiếp tuyến đến đường tròn?
Xem đáp án
Đáp án A
Do đó, điểm A nằm trên đường tròn đã cho. Khi đó, qua điểm A ta vẽ được đúng 1 tiếp tuyến đến đường tròn (I).
Câu 10:
Cho tam giác ABC vuông tại A có AB = 6 cm và BC = 10 cm. Vẽ đường tròn ( A; 6). Hỏi qua C dựng được bao nhiêu tiếp tuyến đến đường tròn?
Xem đáp án
Đáp án C
Áp dụng định lí Pytago vào tam giác ABC ta có:
⇒
⇒ AC = 8cm
Ta có: AC > R (8 > 6) nên điểm C nằm ngoài đường tròn (A ; 6).
Do đó, qua điểm C ta vẽ được hai tiếp tuyến đến đường tròn.