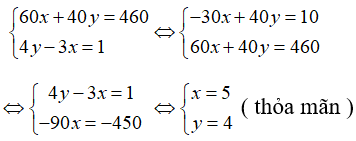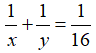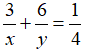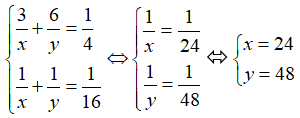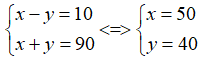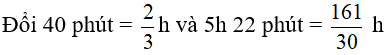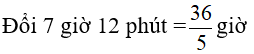Bài 5 (có đáp án): Giải bài toán bằng cách lập hệ phương trình
-
640 lượt thi
-
10 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Cho một số có hai chữ số. Nếu đổi chỗ hai chữ số của nó thì được một số lớn hơn số đã cho là 63. Tổng của số đã cho và số mới tạo thành bằng 99. Tổng các chữ số của số đó là
 Xem đáp án
Xem đáp án
Đáp án A

Vậy số đã cho là 18 và tổng các chữ số của số này là 1 + 8 = 9.
Câu 2:
Cho một số có hai chữ số. Chữ số hàng chục lớn hơn chữ số hàng đơn vị là 5. Nếu đổi chỗ hai chữ số cho nhau ta được một số bằng 3/8 số ban đầu. Tìm tích các chữ số của số ban đầu.
 Xem đáp án
Xem đáp án
Đáp án C

Câu 3:
Một ô tô đi quãng đường AB với vận tốc 50 km/h , rồi đi tiếp quãng đường BC với vận tốc 45 km/h . Biết quãng đường tổng cộng dài 165 km và thời gian ô tô đi trên quãng đường AB ít hơn thời gian đi trên quãng đường BC là 30 phút. Tính thời gian ô tô đi trên đoạn đường AB.
 Xem đáp án
Xem đáp án
Đáp án B
Gọi thời gian ô tô đi trên mỗi đoạn đường AB và BC lần lượt là x; y
(x > 0; y > 0,5; đơn vị: giờ ) .
Vậy thời gian ô tô đi trên quãng đường AB là 1,5 giờ . Thời gian ô tô đi hết quãng đường BC là 2 giờ.
Câu 4:
Trên một cánh đồng cấy 60 ha lúa giống mới và 40 ha lúa giống cũ, thu hoạch được tất cả 460 tấn thóc. Hỏi năng suất lúa mới trên 1 ha là bằng bao nhiêu, biết rằng 3 ha trồng lúa mới thu hoạch được ít hơn 4 ha trồng lúa cũ là 1 tấn
 Xem đáp án
Xem đáp án
Đáp án A
Gọi năng suất lúa mới và lúa cũ trên 1 ha lần lượt là x; y (x, y > 0) đơn vị : tấn/ha
Cấy 60ha lúa giống mới thu hoạch được: 60x (tấn).
Cấy 40ha lúa giống cũ thu hoạch được 40y (tấn)
Vì cấy 60 ha lúa giống mới và 40 ha lúa giống cũ, thu hoạch được tất cả 460 tấn thóc nên ta có
60x + 40y = 460
Vì 3 ha trồng lúa mới thu hoạch được ít hơn 4 ha trồng lúa cũ là 1 tấn nên ta có phương trình
4y - 3x = 1
Suy ra ta có hệ phương trình:
Vậy năng suất lúa mới trên 1 ha là 5 tấn
Câu 5:
Một ô tô dự định đi từ A đến B trong một thời gian nhất định . Nếu xe chạy mỗi giờ nhanh hơn 10km thì đến nơi sớm hơn dự định 3 giờ , còn nếu xe chạy chậm lại mỗi giờ 10km thì đến nơi chậm mất 5 giờ. Tính vận tốc của xe lúc ban đầu
 Xem đáp án
Xem đáp án
Đáp án A
Gọi vận tốc ban đầu là x (km/h); (x > 10). Thời gian chạy dự định là y (giờ)
Chiều dài quãng đường là: x.y
Nếu xe chạy mỗi giờ nhanh hơn 10 km thì đến nơi sớm hơn dự định 3 giờ. Vận tốc xe khi đó là
x + 10 (km /h ); thời gian đi là : y – 3 ( giờ) .
Chiều dài quãng đường là (x + 10)(y - 3)
Nếu xe chạy chậm lại mỗi giờ 10km thì đến nơi chậm mất 5 giờ. Vận tốc xe đi khi đó là: x – 10 ( km/h) và thời gian đi là : y + 5( giờ).
Chiều dài quãng đường là (x - 10)(y + 5)
Suy ra ta có hệ:
Vậy vận tốc ban đầu là 40 km/h
Câu 6:
Hai người thợ cùng làm một công việc trong 16 giờ thì xong. Nếu người thứ nhất làm 3 giờ và người thứ hai làm 6 giờ thì họ làm được một phần tư công việc . Hỏi mỗi người thợ làm một mình thì trong bao nhiêu giờ mới xong công việc đó.
 Xem đáp án
Xem đáp án
Đáp án A
Gọi thời gian người thợ thứ nhất làm một mình xong việc là x(giờ) (x > 16)
Thời gian người thợ thứ hai làm một mình xong việc là y(giờ) (y > 16)
Suy ra trong thời gian 1 giờ người thợ thứ nhất làm được 1/x công việc
Trong thời gian 3 giờ người thợ thứ nhất làm được 3/x công việc
Trong thời gian 1 giờ người thợ thứ hai làm được 1/y công việc
Trong thời gian 6 giờ người thợ thứ hai làm được 6/y công việc
Hai người cùng làm trong 16 giờ thì xong việc, nên 1 giờ cả 2 người làm được 1/16 công việc ta có phương trình:
Người thứ nhất làm 3 giờ và người thứ hai làm 6 giờ thì được một phần tư công việc, ta có phương trình:
Từ đó ta có hệ phương trình:
Kết luận: thời gian người thợ thứ nhất làm một mình xong việc là 24 (giờ)
Thời gian người thợ thứ hai làm một mình xong việc là 48 giờ
Câu 7:
Hai lớp 9A và 9B có tổng số 82 học sinh. Trong dịp tết trồng cây năm 2020, mỗi học sinh lớp 9A trồng được 3 cây, mỗi học sinh lớp 9B trồng được 4 cây nên cả hai lớp trồng được tổng số 288 cây. Tính số học sinh mỗi lớp.
 Xem đáp án
Xem đáp án
Đáp án B
Gọi x, y lần lượt là số học sinh của lớp 9A và lớp 9B (x, y ∈ N*; x, y < 82)
Tổng số học sinh của hai lớp là 82 ⇒ x + y = 82 (1)
Mỗi học sinh lớp 9A và 9B lần lượt trồng được 3 cây và 4 cây nên tổng số cây hai lớp trồng là 3x + 4y (cây). Theo bài ra ta có 3x + 4y = 288 (2)
Từ (1) và (2) ta có hệ phương trình:
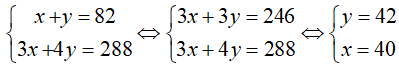
Vậy số học sinh lớp 9A và 9B lần lượt là 40 và 42.
Câu 8:
Một ô tô và một xe máy ở hai địa điểm A và B cách nhau 180 km, khởi hành cùng một lúc đi ngược chiều nhau và gặp nhau sau 2 giờ. Biết vận tốc của ô tô lớn hơn vận tốc của xe máy 10 km/h. Tính vận tốc của ô tô và xe máy lần lượt là?
 Xem đáp án
Xem đáp án
Đáp án D
Gọi vận tốc của ô tô là x (km/h)
Vận tốc của xe máy là y (km/h) ( Điều kiện: x > y > 0, x > 10)
Ta có vận tốc của ô tô lớn hơn vận tốc của xe máy 10 km/h nên : x – y = 10 (1)
Sau 2 giờ ô tô đi được quãng đường là 2x (km)
Sau 2 giờ xe máy đi được quãng đường là: 2y (km)
Sau 2 giờ thì chúng gặp nhau, ta có phương trình: 2x + 2y = 180 hay x + y = 90 (2)
Từ (1), (2) ta có hệ phương trình :
Thỏa mãn điều kiện,vậy vận tốc của ô tô là 50 km/h và vận tốc của xe máy là: 40 km/h
Câu 9:
Hai ô tô cùng khởi hành 1 lúc từ 2 tỉnh A và B cách nhau 400 km đi ngược chiều và gặp nhau sau 5h. Nếu vận tốc của mỗi xe vẫn không thay đổi nhưng xe đi chậm xuất phát trước xe kia 40 phút thì 2 xe gặp nhau sau 5h 22 phút kể từ lúc xe chậm khởi hành. Tính vận tốc của mỗi xe.
 Xem đáp án
Xem đáp án
Đáp án A
Gọi vận tốc của xe nhanh là x km/h
Gọi vận tốc của xe chậm là y km/h (điều kiện: x> y > 0)
Hai xe cùng khởi hành một lúc và đi ngược chiều sau 5h gặp nhau nên ta có phương trình
5(x + y) = 400 (1)
Sau khi thay đổi thời gian ta có
Vậy vận tốc của xe nhanh là 44 km/h
Vận tốc của xe chậm là 36 km/h.
Câu 10:
Hai người cùng làm một công việc trong 7h 12 phút thì xong công việc. Nếu người thứ 1 làm một mình trong 4 giờ và người thứ 2 làm một mình trong 3 giờ thì được 50% công việc. Hỏi mỗi người làm một mình trong mấy giờ thì xong?
 Xem đáp án
Xem đáp án
Đáp án B
Gọi thời gian người thứ 1 làm một mình xong công việc là x (giờ), (điều kiện x > 0).
Gọi thời gian người thứ 2 làm một mình xong việc là y (giờ), ( điều kiện y > 0).
Vậy thời gian người thứ 1 làm một mình xong công việc là 12 giờ
Thời gian người thứ 2 làm một mình xong công việc là 18 giờ.