Dạng 1: Lý thuyết chứng minh đẳng thức hình học có đáp án
-
730 lượt thi
-
56 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
Cho đường tròn (O) đường kính AB = 2R và C là một điểm thuộc đường tròn . Trên nửa mặt phẳng bờ AB có chứa điểm C , kẻ tia Ax tiếp xúc với đường tròn (O), gọi M là điểm chính giữa của cung nhỏ AC . Tia BC cắt Ax tại Q , tia AM cắt BC tại N.
Chứng minh các tam giác BAN và MCN cân .
 Xem đáp án
Xem đáp án
a)
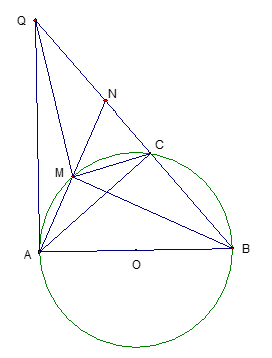
Xét và .
Ta có: AB là đường kính của đường tròn (O)
nên : .
M là điểm chính giữa của cung nhỏ AC
nên . Tam giác ABN có MB vừa là đường cao, đồng thời là đường phân giác nên => cân đỉnh B.
. Tứ giác AMCB nội tiếp.
=> ( cùng bù với ).
=> ( cùng bằng ).
=> Tam giác MCN cân đỉnh M
Câu 2:
a/ nội tiếp.
 Xem đáp án
Xem đáp án
a/
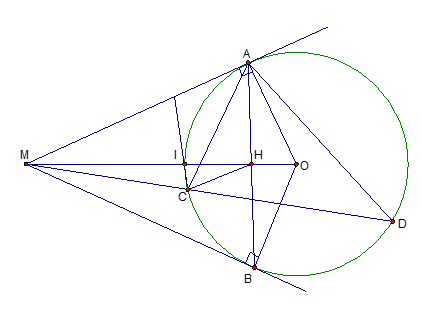
Ta có:
Tứ giác nội tiếp
Câu 4:
 Xem đáp án
Xem đáp án
c/ Ta có:
cân tại O
Mà OH là đường phân giác nên cũng là đường cao
Ta lại có:
Câu 5:
 Xem đáp án
Xem đáp án
d/ Từ
(*)
Xét có:
và chung
đồng dạng (1)
Ta lại có (cùng chắn hai cung bằng nhau) là phân giác của .
Theo t/c đường phân giác của tam giác, ta có: (2)
và có chung và do đó đồng dạng (g.g) (3)
Từ (1), (2), (3) suy ra suy ra CI là tia phân giác của góc .
Câu 6:
Cho đường tròn tâm O , đường kính AB. Trên tiếp tuyến của đường tròn(O) tại A lấy điểm M . Từ vẽ tiếp tuyến thứ hai MC với (O) ( C là tiếp điểm). Kẻ CH vuông góc vớiAB ,MB cắt (O) tại điểm thứ hai là K và cắt CH tại K. Chứng minh rằng:
a/ nội tiếp.
 Xem đáp án
Xem đáp án
a/
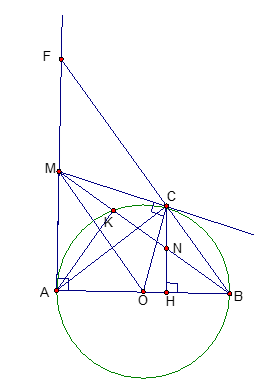
Ta có:
Vậy tứ giác nội tiếp.
Câu 9:
 Xem đáp án
Xem đáp án
d/ Ta có:
(1)
Ta lại có: cân tại
cân tại M.
mà nên (2)
Từ (1) và (2) suy ra
Vậy N là trung điểm CH.
Câu 10:
Cho đường tròn (O), từ một điểm A nằm ngoài đường tròn (O), vẽ hai tia tiếp tuyến AB và AC với đường tròn. Kẻ dây . Nối AD cắt đường tròn (O) tại E. Chứng minh:
a/ nội tiếp.
 Xem đáp án
Xem đáp án
a/ Ta có:
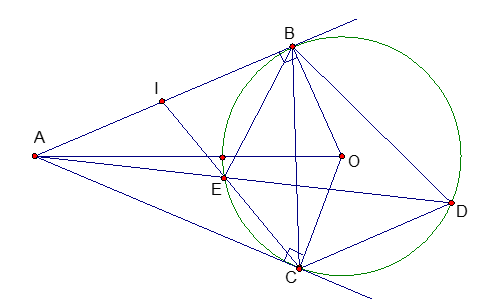
Vậy là tứ giác nội tiếp
Câu 13:
 Xem đáp án
Xem đáp án
d/ Ta có: mà nên
chung
đồng dạng
Ta lại có:
chung
đồng dạng
Mặt khác: nên .
Câu 14:
Cho tứ giác ABCD nội tiếp đường tròn (O;R). Gọi I là giao điểm AC và BD. Kẻ IH vuông góc với AB; IK vuông góc với AD ( ).
a) Chứng minh tứ giác nội tiếp đường tròn.
 Xem đáp án
Xem đáp án
a) Chứng minh tứ giác nội tiếp đường tròn.
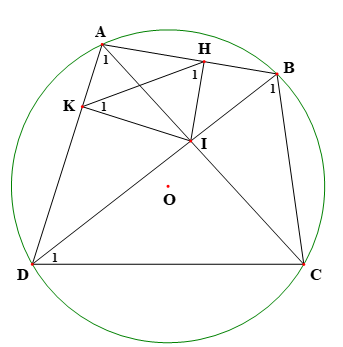
Xét tứ giác có:
Tứ giác nội tiếp.
Câu 15:
b) Chứng minh rằng
 Xem đáp án
Xem đáp án
b) Chứng minh rằng .
Xét và có:
(2 góc nội tiếp cùng chắn cung của )
(2 góc đối đỉnh)
(g.g)
Câu 16:
 Xem đáp án
Xem đáp án
c) Chứng minh rằng tam giác và tam giác đồng dạng.
Xét đường tròn ngoại tiếp tứ giác có
(2 góc nội tiếp cùng chắn cung )
Mà
Chứng minh tương tự, ta được
và có:
(g.g)
Câu 17:
Cho có ba góc nhọn. Đường tròn (O) đường kính BC cắt các cạnh AB, AC lần lượt tại các điểm D và E Gọi H là giao điểm của hai đường thẳng CD và BE
a) Chứng minh tứ giác ADHE nội tiếp trong một đường tròn. Xác định tâm I của đường tròn này.
 Xem đáp án
Xem đáp án
a) Chứng minh tứ giác ADHE nội tiếp trong một đường tròn. Xác định tâm I của đường tròn này.
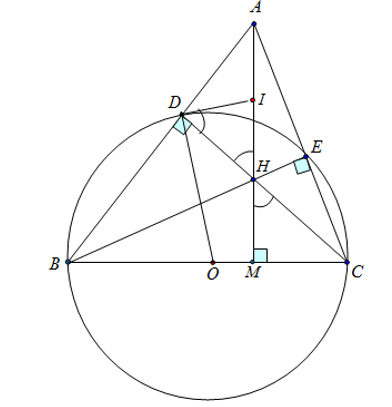
Ta có : (chắn nửa đường tròn)
(chắn nửa đường tròn)
Suy ra :
Xét tứ giác có:
Tứ giác có hai góc đối bù nhau.
Vậy tứ giác nội tiếp trong một đường tròn.
Tâm I là trung điểm cạnh AH
Câu 18:
 Xem đáp án
Xem đáp án
b) Chứng minh
Xét hai tam giác và có :
là góc chung
(chứng minh trên)
Suy ra hai tam giác và đồng dạng
Câu 19:
 Xem đáp án
Xem đáp án
c) Chứng minh ID là tiếp tuyến của đường tròn (O)
Ta có : (do cân tại I)
(đối đỉnh)
Mặt khác : (do cân tại O)
Ngoài ra, trong tam giác vuông MHC có :
Từ suy ra:
Suy ra :
Vậy ID là tiếp tuyến của (O)
Câu 20:
Cho có ba góc nhọn nội tiếp đường tròn (O) . Đường cao CD của cắt đường tròn (O) tại E. Từ B kẻ tại F.
a) Chứng minh tứ giác nội tiếp được đường tròn.
 Xem đáp án
Xem đáp án
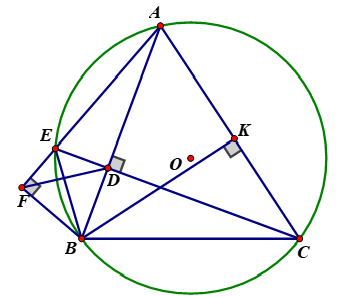
(gt)
(gt)
Vậy tứ giác nội tiếp được đường tròn.
Câu 21:
b) Kẻ đường cao BK của . Chứng minh: .
 Xem đáp án
Xem đáp án
b) Ta có: tứ giác nội tiếp đường tròn (O).
(cùng bù )
Câu 24:
Cho nửa đường tròn (O) đường kính AB=2R , dây cung AC . Gọi M là điểm chính giữa cung AC . Đường thẳng kẻ từ C song song với BM cắt tia AM ở K và cắt tia OM ở D, cắt AC tại H.
1. Chứng minh tứ giác nội tiếp.
 Xem đáp án
Xem đáp án
1. Chứng minh tứ giác nội tiếp.
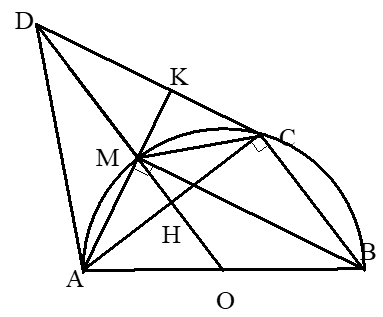
Có (góc nội tiếp chắn nửa đường tròn đường kính AB)
Mà (gt) nên . Vậy .
Lại có (gt) .
Tứ giác có nên tứ giác nội tiếp trong một đường tròn.
Câu 25:
 Xem đáp án
Xem đáp án
2. Chứng minh và
Ta có (góc nội tiếp chắn nửa đường tròn)
Do đó , mà (gt) nên tứ giác là hình bình hành.
Suy ra: và .
Câu 26:
 Xem đáp án
Xem đáp án
3. Xác định vị trí điểm C trên nửa đường tròn (O) để AD là tiếp tuyến của nửa đường tròn.
AD là tiếp tuyến của đường tròn có và
nên M là trực tâm tam giác. Suy ra .
Vậy
Mà nên . Vậy tam giác OBC đều.
Vậy điểm C là điểm thuộc nửa đường tròn sao cho
Câu 27:
Cho đường tròn tâm O đường kính A, M là một điểm nằm trên đoạn thẳng OB ( M khác O và B ). Đường thẳng đi qua M và vuông góc với AB cắt (O) tại C, D. Trên tia MD lấy E nằm ngoài (O). Đường thẳng AE cắt (O) tại điểm I khác A, đường thẳng BE cắt (O) tại điểm K khác B. Gọi H là giao điểm của BI và. Chứng minh:
a) Tứ giác nội tiếp. Xác định tâm đường tròn ngoại tiếp đó.
 Xem đáp án
Xem đáp án
a)
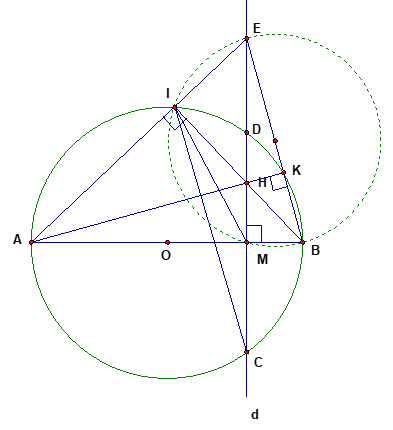
Ta có
Vậy tứ giác nội tiếp đường tròn, tâm của đường tròn là trung điểm của BE.
Câu 30:
 Xem đáp án
Xem đáp án
d) H là trực tâm của tam giác nên
Vìnên ba điểm thẳng hàng.
Do A cố định nên HK luôn đi qua điểm Acố định.
Câu 31:
Cho đường tròn tâm O bán kính R, hai đường kính AB và CD vuông góc với nhau. Trên đoạn AB lấy điểm M khác O, đường thẳng CM cắt đường tròn tại N. Đường thẳng vuông góc với AB tại M cắt tiếp tuyến với dường tròn tại N ở điểm P.
a) Chứng minh: Tứ giác nội tiếp.
 Xem đáp án
Xem đáp án
a) Ta có: cùng thuộc đường tròn đường kính PO.
Vậy tứ giác nội tiếp.

Câu 32:
b) Chứng minh: , suy ra OMPD là hình chữ nhật.
 Xem đáp án
Xem đáp án
b) Ta có: ( tứ giác nội tiếp)
( tam giác cân tại O)
Ta có ; (cùng vuông góc với AB)
là hình bình hành
Mặt khác: nên là hình chữ nhật
Câu 36:
Cho đường tròn (O,R) và AB dây , vẽ đường kính CD vuông góc với AB tại K ( D thuộc cung nhỏ AB). Lấy điểm thuộc cung nhỏ BC , DM cắt AB tại F.
a. Chứng minh tứ giác nội tiếp.
 Xem đáp án
Xem đáp án
a)
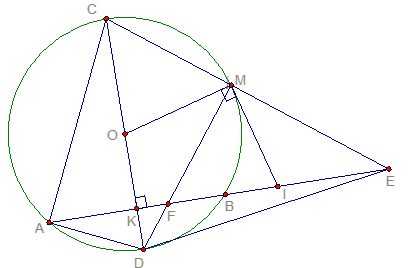
Vì ;
Mà (Góc n.tiếp chắn nửa đường tròn )
Tứ giác nội tiếpCâu 37:
b. Chứng minh: .
 Xem đáp án
Xem đáp án
b) Ta có (Do )
và (Pitago trong tam giác vuông ADC có AK đường cao)
Suy ra: .
Câu 38:
c. Tia cắt CM đường thẳng AB tại E. Tiếp tuyến tại M của (O) cắt AF tại I. Chứng minh: IE=IF
 Xem đáp án
Xem đáp án
c) cân tại (1)
Mà ; ( Vì vuông tạiM )
Mặt khác theo c/m trên: cân tại I;
Từ (1) và (2) suy ra: .
Câu 39:
 Xem đáp án
Xem đáp án
d) Ta có (T/c đường kính vuông góc dây cung)
Ta có: .
Mà (Pitago trong tam giác vuông có là BK đường cao)
Câu 40:
Cho tam giác ABC vuông tại A và đường cao AH. Dựng đường tròn tâm O đường kính AH cắt AB tại E , AC cắt tại F . Các tiếp tuyến với đường tròn (O) tại E, F lần lượt cắt cạnh BC tại M và N.
a) Chứng minh rằng tứ giác nội tiếp
 Xem đáp án
Xem đáp án
a) Chứng minh rằng tứ giác nội tiếp
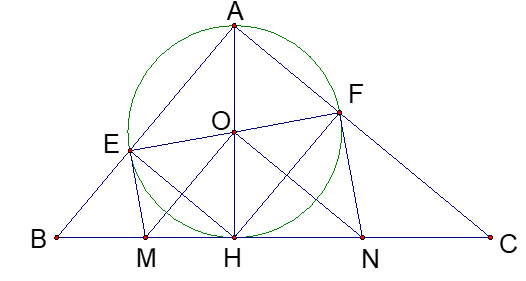
Ta có: (EM là tiếp tuyến của (O))
( AH là đường cao)
Vậy tứ giác nội tiếp
Câu 41:
 Xem đáp án
Xem đáp án
b) Chứng minh rằng
Xét vuông tại H và vuông tại E có:
chung
Vậy
hay
Câu 42:
 Xem đáp án
Xem đáp án
c) Chứng minh ba điểm thẳng hàng.
Ta có:
Suy ra tứ giác là hình chữ nhật
Suy ra là hai đường chéo
Mà O là trung điểm của AH nên O cũng là trung điểm của EF
Vậy ba điểm thẳng hàng.
Câu 43:
 Xem đáp án
Xem đáp án
d) Cho , . Tính diện tích .
Ta có OM là đường trung bình của nên
Tương tự, ta cũng có
OM là tia phân giác của (tính chất hai tiếp tuyến cắt nhau)
Tương tự ta có
Mặt khác (kề bù)
Suy ra vuông tại .
Câu 44:
Cho tam giác ABC vuông cân tại A, nội tiếp trong đường tròn tâm O. Tiếp tuyến tại B với đường tròn (O) cắt tia CA tại D. Trên cạnh AB lấy điểm E ( E không trùng với A và B). Tia CE cắt đường tròn (O) tại F và cắt BD tại K . Tia BF cắt CD tại M.
a) Chứng minh .
 Xem đáp án
Xem đáp án
a) Chứng minh .
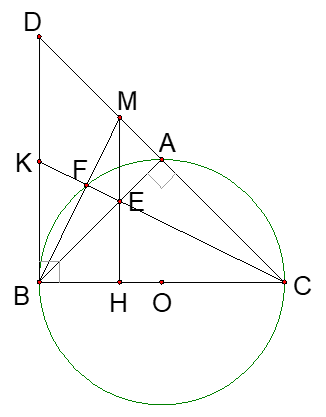
Ta có:
( cùng chắn cung AF)
Vậy (g.g).
Câu 45:
 Xem đáp án
Xem đáp án
b) Chứng minh tứ giác nội tiếp.
Do vuông cân tại A nên
(cùng chắn cung AC )
vuông cân tại B có
Lại có (kề bù)
. Vậy tứ giác nội tiếp
Câu 46:
 Xem đáp án
Xem đáp án
c) Tứ giác MDBH là hình gì?
Ta có E là trực tâm của
(vì cùng vuông góc với BC )
Từ suy ra tứ giác là hình thang vuông.
Câu 48:
Cho đường tròn (O,R) và hai đường kính AB,CD bất kì. Tiếp tuyến tại A của đường tròn (O) cắt các đường thẳng BC và BD lần lượt tại E,F. Gọi P,Q lần lượt là trung điểm của các đường thẳng AE, AF.
a) Chứng minh tứ giác CDEF nội tiếp.
 Xem đáp án
Xem đáp án
a) Tứ giác nội tiếp
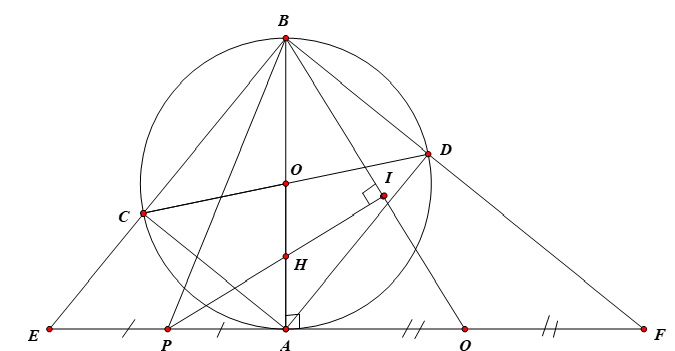
(góc nội tiếp chắn nửa đường tròn)
(vì cùng phụ )
có nên cân tại
Suy ra: tứ giác nội tiếp (có góc trong bằng góc ngoài tại đỉnh đối diện)
Câu 49:
b) Chứng minh rằng và
 Xem đáp án
Xem đáp án
b) và
Áp dụng hệ thức lượng trong tam giác vuông có:
và
Do đó
Ta lại có:
Vậy:
Câu 50:
 Xem đáp án
Xem đáp án
c) H là trung điểm AD
Kẻ và PI cắt AB tại là trực tâm của .
Ta có:
Mà (cùng phụ với )
mà hai góc ở vị trí đồng vị nên
Trong có:
Câu 51:
Cho đường tròn (O,R) đường kính AB=2R dây cung MN của (O) vuông góc AB với tại I sao cho IA<IB. Trên đoạn MI lấy điểm . Tia AE cắt đường tròn tại điểm thứ hai là K
a) Chứng minh tứ giác nội tiếp được đường tròn.
 Xem đáp án
Xem đáp án
a) Tứ giác nội tiếp.
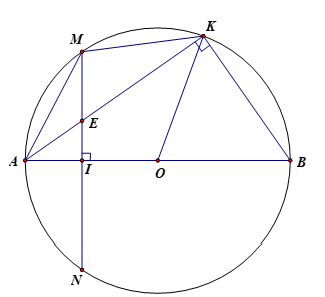
Ta có: (góc nội tiếp chắn nửa đường tròn)
Tứ giác nội tiếp được đường tròn.
Câu 52:
b) Chứng minh
 Xem đáp án
Xem đáp án
b)
Ta có: tại
(hai góc nội tiếp cùng chắn hai cung bằng nhau)
và có:
Câu 53:
c) Chứng minh
 Xem đáp án
Xem đáp án
c)
(góc nội tiếp chắn nửa đường tròn), áp dụng hệ thức lượng trong tam giác vuông có:
Do đó:Câu 54:
Cho nửa đường tròn tâm O, đường kính AB = 2R. Trên tia đối của tia AB lấy điểm E (khác với điểm A). Tiếp tuyến kẻ từ điểm E cắt các tiếp tuyến kẻ từ điểm A và B của nửa đường tròn (O) lần lượt tại C và D. Gọi M là tiếp điểm của tiếp tuyến kẻ từ điểm E.
a) Chứng minh rằng tứ giác ACMO nội tiếp được trong một đường tròn.
 Xem đáp án
Xem đáp án
a) Chứng minh rằng tứ giác ACMO nội tiếp được trong một đường tròn.
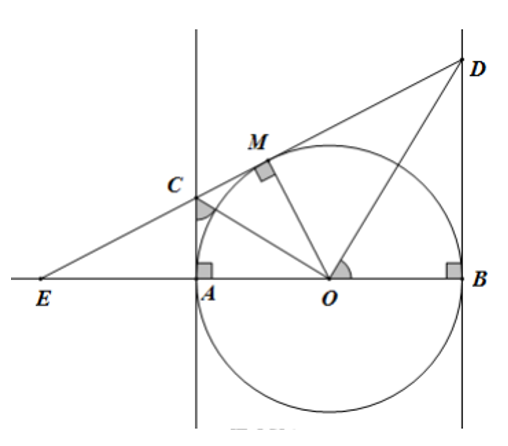
Vì AC là tiếp tuyến của (O) nên OA ⊥ AC =>
Vì MC là tiếp tuyến của (O) nên OM ⊥ MC =>
=> Suy ra OACM là tứ giác nội tiếp
Câu 55:
b) Chứng minh rằng
 Xem đáp án
Xem đáp án
b) Chứng minh rằng
Xét hai tam giác vuông OAC và OMC có
(cạnh huyền – cạnh góc vuông)
⇒ CA = CM .
Tương tự ta có
Mà AC // BD (cùng vuông góc AB) nên
Câu 56:
c) Chứng minh rằng khi điểm E thay đổi trên tia đối của tia AB, tích AC.BD không đổi.
 Xem đáp án
Xem đáp án
c) Chứng minh rằng khi điểm E thay đổi trên tia đối của tia AB, tích AC.BD không đổi.
Vì
Tương tự:
Suy ra
Mà
(không đổi, đpcm)
