Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 7
-
11708 lượt thi
-
6 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Giải các phương trình sau
1) 2(2x − 1) − x = 4.
2) + = .
 Xem đáp án
Xem đáp án
1) Ta có: 2(2x − 1) − x = 4
4x – 2 – x = 4
4x – x = 4 +2
3x = 6
x = 2
Vậy tập nghiệm của phương trình là S = {2}.
2) Ta có: + =
ĐKXĐ: x ≠ 2 và x ≠ 0
+ =
+ =
x.(x + 1) + x – 2 = 5x – 4
x2 + x + x – 2 = 5x – 4
x2 + x + x – 5x – 2 + 4 = 0
x2 – 3x + 2 = 0
x2 – x – 2x + 2 = 0
x(x – 1) – 2(x – 1) = 0
(x – 1). (x – 2) = 0
Ta thấy chỉ có x = 1 thỏa mãn điều kiện.
Vậy tập nghiệm của phương trình là S = {1}.
Câu 2:
Giải các bất phương trình sau và biểu diễn tập nghiệm trên trục số.
1) 3(x + 2) > 2x − 1.
2) − ≥ + 3.
 Xem đáp án
Xem đáp án
1) Ta có: 3(x + 2) > 2x – 1
3x + 6 > 2x – 1
3x – 2x > – 1 – 6
x > – 7.
Vậy bất phương trình có tập nghiệm là S = (–7; +∞).
Biểu diễn tập nghiệm của bất phương trình trên trục số là:
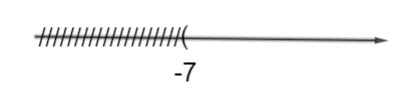
2) Ta có: − ≥ + 3 (1)
Nhân cả hai vế của bất phương trình (1) với 12 ta được:
− ≥ + 3.12
− ≥ + 3.12
6. (x + 1) – 4. (3x – 5) ≥ 3x + 36
6x + 6 – 12x + 20 ≥ 3x + 36
6x – 12x – 3x ≥ 36 – 6 – 20
– 9x ≥ 10
x ≤ .
Vậy tập nghiệm của bất phương trình là:
Biểu diễn tập nghiệm của bất phương trình là:
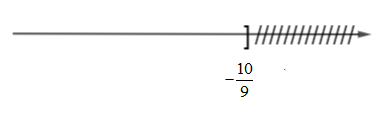
Câu 3:
Giải bài toán sau bằng cách lập phương trình
Một xưởng dệt theo kế hoạch mỗi ngày phải dệt 30 áo. Thực tế xưởng đã dệt được mỗi ngày 40 áo nên đã hoàn thành trước thời hạn 3 ngày, ngoài ra còn dệt thêm được 20 chiếc áo. Tính số áo xưởng phải dệt theo kế hoạch?
 Xem đáp án
Xem đáp án
Gọi x (áo) là số áo mà xưởng phải dệt theo kế hoạch (x ∈ ℕ*)
Theo kế hoạch xưởng sẽ dệt xong số áo trong (ngày)
Thực tế, số áo may được là x + 20 (cái)
Số ngày thực tế là: (ngày)
Vì xưởng đã hoàn thành trước thời hạn 3 ngày nên:
= + 3
– =
40x – 30x = 4200
x = 420 (cái áo)
Vậy số áo xưởng phải dệt theo kế hoạch phân là 420 cái áo.
Câu 4:
1) Tìm x, y trong hình vẽ bên
(Học sinh không phải vẽ lại hình)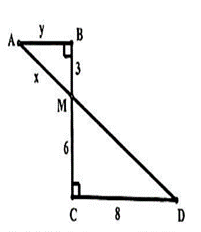
 Xem đáp án
Xem đáp án
Áp dụng định lý Pytago vào ∆ DCM vuông tại C ta được:
DM2 = CM2 + CD2 = 62 + 82 = 100
DM = 10
Xét ∆ ABM và ∆ DCM ta có:
= (2 góc đối đỉnh)
= = 90°
Do đó ∆ABM ᔕ ∆DCM (g.g)
= =
= =
y = = 4
x = = 5
Vậy x = 5 và y = 4.
Câu 5:
Cho tam giác ABC vuông tại A (AB < AC), đường cao AH (H ∈ BC).
a) Chứng minh: ∆ ABC đồng dạng với ∆ HBA.
b) Lấy điểm M thuộc AH. Kẻ đường thẳng đi qua B và vuông góc với CM tại K.
Chứng minh: CM. CK = CH. CB
c) Tia BK cắt HA tại D. Chứng minh = .
 Xem đáp án
Xem đáp án
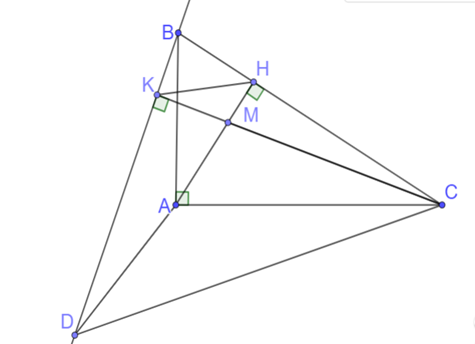
a) Vì ∆ ABC vuông tại A nên = 90°
Vì AH ⊥ BC nên = 90°
Xét ∆ ABC và ∆ HBA ta có:
Chung
= = 90°
Do đó ∆ ABC ᔕ ∆ HBA (g.g)
b) Vì AH ⊥ BC nên = 90°
Vì AM ⊥ BD tại K nên = 90°
Xét ∆CHM và ∆CBK ta có:
Chung
= = 90°
Do đó ∆ CHM ᔕ ∆ CBK (g.g)
=
CH. CK = CM. CB (đpcm)
c) Xét ∆CMH và ∆DMK, có:
(2 góc đối đỉnh)
⇒ ∆CMH ᔕ ∆DMK (g – g)
⇒ (hai cạnh tương ứng)
⇒
Xét ∆MHK và ∆MCD, có:
(cmt)
(2 góc đối đỉnh)
⇒ ∆MHK ᔕ ∆MCD (c – g – c)
⇒ (2 góc tương ứng)
Ta lại có:
(∆CDH vuông tại H)
(hai góc phụ nhau)
Mà (cmt)
hay = .
Câu 6:
Giải bất phương trình sau:
3x3 − 5x2 − x − 2 > 0.
 Xem đáp án
Xem đáp án
Ta có: 3x3 − 5x2 − x − 2 > 0
3(x3 − 8) − 5 (x2 − 4) − x + 2 > 0
3(x − 2) (x2 + 2x + 4) − 5 (x − 2) (x + 2) – (x – 2) > 0
(x – 2) (3x2 + 6x + 12 – 5x – 10 – 1) > 0
(x – 2) (3x2 + x + 1) > 0 (*)
Ta có: 3x2 + x + 1 = 3 = 3 > 0, ∀x
Vậy (*) x – 2 > 0 x > 2
Vậy tập nghiệm của bất phương trình đã cho là S = {x | x > 2}.
