20 câu hỏi trắc nghiệm thuộc Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 18

Câu 1:

Bất phương trình nào là bất phương trình bậc nhất một ẩn?

A. $\frac{1}{x} - 1 > 0;$

B. $\frac{1}{2} x + 2 < 0;$

C. 2x² + 3 > 0;

D. 2x + 1 - 2(x + 3) > 0.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: B

Bất phương trình dạng ax + b < 0 (hoặc ax + b > 0, ax + b ≤ 0, ax + b ≥ 0) trong đó a và b là hai số đã cho, a ≠ 0, được gọi là bất phương trình bậc nhất một ẩn

+) $\frac{1}{x} - 1 > 0 \Leftrightarrow \frac{1 - x}{x} > 0$

Þ Không là bất phương trình bậc nhất một ẩn

+) $\frac{1}{2} x + 2 < 0 \Leftrightarrow \frac{x + 4}{2} < 0 \Leftrightarrow x + 4 < 0$

Þ Là một bất phương trình bậc nhất một ẩn

+) 2x² + 3 > 0

Þ Là một bất phương trình bậc hai một ẩn

+) 2x + 1 - 2(x + 3) > 0 Û 2x + 1 - 2x - 6 > 0

Û -5 > 0

Þ Không là bất phương trình bậc nhất một ẩn.

Câu 2:

Giá trị k sao cho phương trình 2x + k = x - 1 có nghiệm x₀ = -2 là

A. k = -2;

B. k = -1;

C. k = 1;

D. k = 2.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: C

Để phương trình 2x + k = x - 1 có nghiệm x₀ = -2 nên suy ra

2x₀ + k = x₀ - 1

Û k = - x₀ - 1 = -(-2) - 1

Û k = 1.

Câu 3:

Tập nghiệm của phương trình x² - 3x = 0 là

A. S = {0};

B. S = {0; 3};

C. S = {3};

D. S = {0; -3}.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: B

x² - 3x = 0

Û x(x - 3) = 0

$\Rightarrow [\begin{matrix} x = 0 \\ x - 3 = 0 \end{matrix} \Leftrightarrow [\begin{matrix} x = 0 \\ x = 3 \end{matrix}$

Vậy tập nghiệm của phương trình là S = {0; 3}.

Câu 4:

Điều kiện xác định của phương trình $\frac{x}{x - 2} = \frac{2 x}{x^{2} - 1}$

A. x ¹ -1; x ¹ 2;

B. x ¹ 0;

C. x ¹ 2; x ¹ ±1;

D. x ¹ 1; x ¹ 2.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: C

$\frac{x}{x - 2} = \frac{2 x}{x^{2} - 1}$

$\Leftrightarrow \frac{x}{x - 2} = \frac{2 x}{(x - 1) (x + 1)}$

Ta có điều kiện xác định của phương trình là:

$\{\begin{matrix} x - 2 \neq 0 \\ x - 1 \neq 0 \\ x + 1 \neq 0 \end{matrix} \Leftrightarrow \{\begin{matrix} x \neq 2 \\ x \neq 1 \\ x \neq - 1 \end{matrix}$

Vậy suy ra x ¹ 2; x ¹ ±1.

Câu 5:

Tập nghiệm của bất phương trình 5 - 2x ³ 0 là

A. $\{x | x \geq \frac{5}{2}\};$

B. $\{x | x \geq - \frac{5}{2}\};$

C. $\{x | x \leq - \frac{5}{2}\};$

D. $\{x | x \leq \frac{5}{2}\} .$

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: D

Ta có: 5 - 2x ³ 0 Û 2x £ 5

$\Leftrightarrow x \leq \frac{5}{2}$

Vậy tập nghiệm của bất phương trình 5 - 2x ³ 0 là $S = \{x | x \leq \frac{5}{2}\} .$

Câu 6:

Giá trị x = 2 là nghiệm của phương trình

A. 3x + 3 = 9;

B. -5x = 4x + 1;

C. x - 2x = -2x + 4;

D. x - 6 = 5 - x.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: A

+) 3x + 3 = 9 Û 3x = 6

Û x = 2

Suy ra nghiệm của phương trình là x = 2

+) -5x = 4x + 1 Û 9x = -1

$\Leftrightarrow x = \frac{- 1}{9}$

Suy ra nghiệm của phương trình là $x = \frac{- 1}{9}$

+) x - 2x = -2x + 4

Û x = 4

Suy ra nghiệm của phương trình là x = 4

+) x - 6 = 5 - x Û 2x = 11

$\Leftrightarrow x = \frac{11}{2}$

Suy ra nghiệm của phương trình là $x = \frac{11}{2} .$

Câu 7:

Phương trình |x - 3| = 9 có tập nghiệm là

A. {-6; 12};

B. {6};

C. {12};

D. {-12}.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: A

|x - 3| = 9

$\Leftrightarrow [\begin{matrix} x - 3 = 9 \\ x - 3 = - 9 \end{matrix} \Leftrightarrow [\begin{matrix} x = 9 + 3 = 12 \\ x = - 9 + 3 = - 6 \end{matrix}$

Vậy suy ra phương trình |x - 3| = 9 có tập nghiệm là {-6; 12}.

Câu 8:

Nếu -2a > -2b thì

A. a < b;

B. a = b;

C. a > b;

D. a £ b.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: A

-2a > -2b

Û a < b (Chia 2 vế của bất phương trình cho -2).

Câu 9:

Cho hình vẽ, biết AB = BC = 5 cm, DC = 8 cm. Diện tích của tam giác HBC là

A. 4,5 cm²;

B. 6 cm²;

C. 12 cm²;

D. 16 cm².

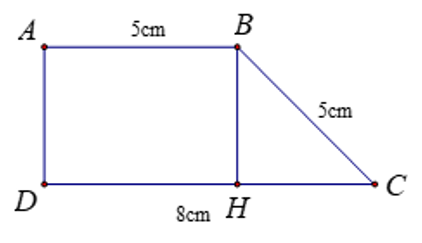
Xem đáp án

Hướng dẫn giải

Đáp án đúng là: B

ABHD là hình chữ nhật nên suy ra AB = DH = 5 cm.

+) HC = DC - DH = 8 - 5 = 3 (cm)

+) Áp dụng định lý Pytago vào tam giác BHC vuông tại H ta có

$B H = \sqrt{B C^{2} - H C^{2}} = \sqrt{5^{2} - 3^{2}} = 4 (c m)$

Khi đó diện tích tam giác vuông BHC là

$S_{B H C} = \frac{1}{2} B H . H C = \frac{1}{2} 4.3 = 6 (c m^{2}) .$

Câu 10:

Cho tam giác ABC có AB = 30 cm, AC = 45 cm, BC = 50 cm, đường phân giác AD (D Î BC). Độ dài BD là

A. BD = 20 cm;

B. BD = 30 cm;

C. BD = 10 cm;

D. BD = 25 cm.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: A

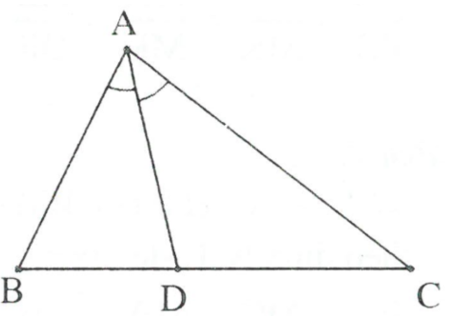
Cho tam giác ABC có AB = 30 cm, AC = 45 cm, BC = 50 cm, đường phân giác AD (D thuộc BC). Độ dài BD là (ảnh 1)

Áp dụng định lý đường phân giác ta có:

$\frac{B D}{D C} = \frac{A B}{A C} = \frac{30}{45} = \frac{2}{3} \Rightarrow D C = \frac{3}{2} B D$

Mà ta có:

BC = BD + DC

$\Rightarrow B D + \frac{3}{2} B D = 50$

$\Leftrightarrow \frac{5}{2} B D = 50$

$\Leftrightarrow B D = 50. \frac{2}{5} = 20 (c m)$ .

Câu 11:

Cho tam giác ABC đồng dạng với tam giác MNP theo tỉ số 2. Khẳng định đúng là

A. MN = 2.AB;

B. AC = 2.NP;

C. MP = 2.BC;

D. BC = 2.NP.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: D

Vì ΔABC ᔕ ΔMNP theo tỉ số k = 2

$\Rightarrow \frac{M N}{A B} = \frac{1}{2}$

Nên ΔMNP ᔕ ΔABC theo tỉ số

$\frac{M N}{A B} = \frac{1}{2} \Leftrightarrow A B = 2. M N$

Tương tự ta có: BC = 2.NP và AC = 2.MP.

Câu 12:

Hình dưới đây mô tả cách đo chiều cao của cây. Các thông số đo đạc được như sau: AB = 1 m; AA' = 4,5 m; CA = 1,2 m. Chiều cao của cây là

A. 5 (m);

B. 4,5 (m);

C. 6,6 (m);

D. 4 (m).

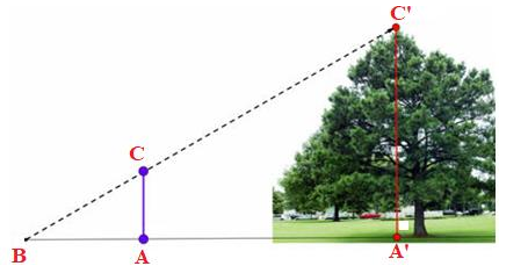
Xem đáp án

Hướng dẫn giải

Đáp án đúng là: C

Áp dụng hệ quả của định lý Ta lét với AC // A'C', ta có:

$\frac{A B}{B A'} = \frac{A B}{A B + A A'} = \frac{A C}{A' C'}$

$\Rightarrow A' C' = \frac{(A B + A A') . A C}{A B}$

$\Leftrightarrow A' C' = \frac{(1 + 4,5) .1,2}{1} = 6,6$ (m).

Vậy chiều cao của cây là 6,6 m.

Câu 13:

Giải các phương trình và bất phương trình sau:

a) (x + 2)(3x - 15) = 0;

Xem đáp án

Hướng dẫn giải

a) (x + 2)(3x - 15) = 0

$\Leftrightarrow [\begin{matrix} x + 2 = 0 \\ 3 x - 15 = 0 \end{matrix}$

$\Leftrightarrow [\begin{matrix} x = - 2 \\ x = \frac{15}{3} = 5 \end{matrix}$

Vậy tập nghiệm của phương trình là: S = {-2; 5}.

Câu 14:

Giải các phương trình và bất phương trình sau:

b) $\frac{3}{x + 1} - \frac{2}{x - 2} = \frac{4 x - 2}{(x + 1) . (x - 2)};$

Xem đáp án

b) $\frac{3}{x + 1} - \frac{2}{x - 2} = \frac{4 x - 2}{(x + 1) . (x - 2)}$

ĐKXĐ: $\{\begin{matrix} x + 1 \neq 0 \\ x - 2 \neq 0 \end{matrix} \Leftrightarrow \{\begin{matrix} x \neq - 1 \\ x \neq 2 \end{matrix}$

Phương trình đã cho trở thành:

$\frac{3 (x - 2) - 2 (x + 1)}{(x + 1) . (x - 2)} = \frac{4 x - 2}{(x + 1) . (x - 2)}$

$\Leftrightarrow \frac{3 x - 6 - 2 x - 2}{(x + 1) . (x - 2)} = \frac{4 x - 2}{(x + 1) . (x - 2)}$

$\Leftrightarrow \frac{x - 8}{(x + 1) . (x - 2)} = \frac{4 x - 2}{(x + 1) . (x - 2)}$

Þ x - 8 = 4x - 2

Û 3x = -6 Û x = -2 (thỏa mãn ĐKXĐ)

Vậy nghiệm của phương trình là x = -2.

Câu 15:

Giải các phương trình và bất phương trình sau:

c) $\frac{2 x + 2}{3} < 2 + \frac{x - 2}{2} .$

Xem đáp án

c) $\frac{2 x + 2}{3} < 2 + \frac{x - 2}{2}$

$\Leftrightarrow \frac{2 x + 2}{3} - 2 < \frac{x - 2}{2}$

$\Leftrightarrow \frac{2 x + 2 - 6}{3} < \frac{x - 2}{2}$

$\Leftrightarrow \frac{2 x - 4}{3} < \frac{x - 2}{2}$

Û 2(2x - 4) < 3(x - 2)

Û 4x - 8 < 3x - 6

Û 4x - 3x < 8 - 6 Û x < 2

Vậy tập nghiệm của bất phương trình là S = (-¥; 2).

Câu 16:

Một nhóm học sinh có kế hoạch làm mặt nạ chắn giọt bắn tiếp sức cho các y bác sỹ phòng chống dịch bệnh Covid-19. Theo kế hoạch, mỗi ngày nhóm làm 80 chiếc mặt nạ. Khi thực hiện, nhờ tinh thần hăng say làm việc, mỗi ngày nhóm đã làm thêm được 10 chiếc mặt nạ. Do đó nhóm hoàn thành trước kế hoạch 1 ngày. Tính tổng số mặt nạ chắn giọt bắn mà nhóm học sinh dự kiến làm?

Xem đáp án

Hướng dẫn giải

Gọi x (ngày) là số ngày theo kế hoạch mà nhóm cần để hoàn thành việc làm mặt nạ (x Î ℕ*, x > 1).

Vậy theo kế hoạch, 1 ngày nhóm cần làm 80 chiếc thì suy ra số chiếc mặt nạ mà nhóm cần làm là: 80x (mặt nạ).

Vì mỗi ngày nhóm đã làm thêm được 10 chiếc mặt nạ nên nhóm hoàn thành trước kế hoạch 1 ngày.

Do đó số mặt nạ nhóm cần làm là: 90(x - 1) (mặt nạ).

Khi đó, ta lập được phương trình:

80x = 90(x - 1)

Û 80x = 90x - 90

Û 90x - 80x = 90

Û 10x = 90 Û x = 9 (TMĐK)

Do đó số chiếc mặt nạ mà nhóm đó cần phải làm là:

80.9 = 720 (chiếc).

Vậy nhóm đó cần phải làm là 720 chiếc mặt nạ.

Câu 17:

Cho tam giác KBC vuông tại K (KB < KC). Tia phân giác của B cắt cạnh KC

tại H. Qua C vẽ đường thẳng vuông góc với tia BH cắt đường thẳng BH tại I.

1. Chứng minh tam giác BHK đồng dạng với tam giác CHI;

Xem đáp án

Hướng dẫn giải

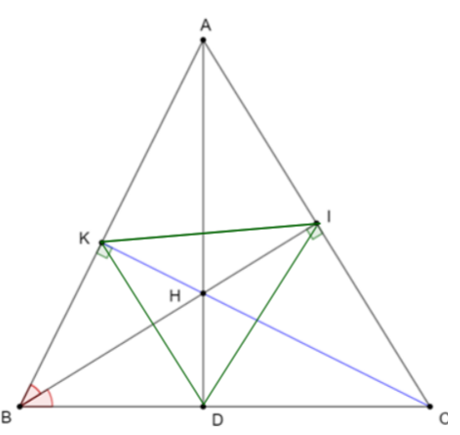
Cho tam giác KBC vuông tại K (KB < KC). Tia phân giác của B cắt cạnh KC tại H. (ảnh 1)

1. Xét tam giác BHK và tam giác CHI có:

$\begin{matrix} \hat{B H K} = \hat{C H I} \\ \hat{B K H} = \hat{C I H} (= 90 °) \end{matrix}\} \Rightarrow Δ B H K ∽ Δ C H I (g . g)$

Câu 18:

2. Chứng minh CI² = IH.IB;

Xem đáp án

2. Từ câu a: DBHK ᔕ DCHI

Suy ra $\hat{K B H} = \hat{I C H}$ (hai góc tương ứng).

Mà $\hat{K B H} = \hat{I B C}$ (do BI là đường phân giác $\hat{A B C}$ )

Nên suy ra $\hat{I C H} = \hat{I B C} (= \hat{K B H})$

Xét tam giác ICH và tam giác IBC có:

$\begin{matrix} \hat{I C H} = \hat{I B C} (= \hat{K B H}) \\ \hat{C I H} = \hat{B I C} (= 90 °) \end{matrix}\} \Rightarrow Δ C I H ∽ Δ B I C (g . g)$

$\Rightarrow \frac{C I}{B I} = \frac{I H}{I C} \Rightarrow C I^{2} = I H . I B$ (đpcm)

Câu 19:

3. Tia BK cắt tia CI tại A, tia AH cắt BC tại D. Chứng minh KC là tia phân giác của IKD

Xem đáp án

3. BI và CK là hai đường cao của tam giác ABC nên H là giao BI và CK nên là trực tâm của tam giác ABC

Suy ra AD ^ BC.

+) Xét tứ giác BKIC có hai góc vuông $\hat{B K C}, \hat{B I C}$ cùng nhìn cạnh BC nên BKIC nội tiếp đường tròn.

Suy ra $\hat{I B C} = \hat{I K C}$ (hai góc cùng chắn cung $\overset{⏜}{I C}$ ) (1)

+) Xét tứ giác BKHD có tổng hai góc đối $\hat{B K H}, \hat{B D H}$ bằng 180° nên BKHD nội tiếp đường tròn

Suy ra $\hat{H B D} = \hat{H K D}$ (hai góc cùng chắn cung $\overset{⏜}{H D}$ ) (2)

Từ (1) và (2) suy ra $\hat{H K I} = \hat{H K D} (= \hat{H B D})$ .

Vậy suy ra KC là tia phân giác của IKD.

Câu 20:

Cho 4a² + b² = 5ab và 2a > b > 0. Tính giá trị của biểu thức

$A = \frac{a b}{4 a^{2} - b^{2}} .$

Xem đáp án

Hướng dẫn giải

Ta có: 4a² + b² = 5ab

Û 4a² - 5ab + b² = 0

Û 4a² - 4ab - ab + b² = 0

Û 4a(a - b) - b(a - b) = 0

Û (a - b)(4a - b) = 0

$\Rightarrow [\begin{matrix} a - b = 0 \\ 4 a - b = 0 \end{matrix} \Leftrightarrow [\begin{matrix} a = b \\ 4 a = b \end{matrix}$

Đối chiếu điều kiện 2a > b > 0 nên suy ra a = b.

Khi đó: $A = \frac{a b}{4 a^{2} - b^{2}} = \frac{a . a}{4 a^{2} - a^{2}}$

$= \frac{a^{2}}{4 a^{2} - a^{2}} = \frac{a^{2}}{3 a^{2}} = \frac{1}{3} .$

Vậy $A = \frac{a b}{4 a^{2} - b^{2}} = \frac{1}{3}$ .

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đề kiểm tra cuối kì 2 Toán 8 có đáp án ( Mới nhất)

Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 18

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương