Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 19
-
11696 lượt thi
-
10 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Cho biểu thức (với x ¹ ± 5)
1. Rút gọn biểu thức A.
 Xem đáp án
Xem đáp án
Hướng dẫn giải
ĐKXĐ:
1.
với x ¹ ± 5
Câu 2:
2. Tìm giá trị của x để |A| = A.
 Xem đáp án
Xem đáp án
2. Với x ¹ ± 5.
Để |A| = A nên suy ra A ³ 0
Û x > -5
Kết hợp ĐKXĐ. Vậy với x > -5, x ¹ 5 thì |A| = A.
Câu 3:
1. Giải các phương trình sau:
a. 9x + 12 = 3x - 6
 Xem đáp án
Xem đáp án
Hướng dẫn giải
1.
a) 9x + 12 = 3x - 6
Û 9x - 3x = -6 - 12
Û 6x = -18
Û x = -3
Vậy nghiệm của phương trình là x = -3.
Câu 4:
Giải các phương trình sau:
b.
 Xem đáp án
Xem đáp án
b) ĐKXĐ:
Khi đó phương trình đã cho tương đương với:
Þ -2x2 - x - 1 = x2 - 1
Û 3x2 + x = 0
Û x(3x + 1) = 0
Vậy nghiệm của phương trình là
Câu 5:
2. Giải bất phương trình sau và biểu diễn tập nghiệm trên trục số:
 Xem đáp án
Xem đáp án
2.
Þ 9 - 3x > 3
Û 3x < 6 Û x < 2
Vậy tập nghiệm của bất phương trình là S = {x | x < 2}.
Khi đó ta có biểu diễn tập nghiệm trên trục số như sau:

Câu 6:
Một ô tô đi từ A đến B với vận tốc trung bình 45 km/h. Lúc ô tô đi từ B về A với vận tốc trung bình là 40 km/h, biết tổng thời gian cả đi lẫn về là 8h 30 phút. Tính độ dài quãng đường AB.
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Ta có 8h 30 phút = h.
Gọi x (km) là độ dài quãng đường AB (x > 0)
Thời gian ô tô đi từ A đến B với với vận tốc trung bình 45 km/h là
Thời gian ô tô đi từ B về A với với vận tốc trung bình 40 km/h là
Tổng thời gian cả đi cả về của ô tô đó là 8h 30 phút hay h nên ta có phương trình:
(TMĐK)
Vậy quãng đường AB dài là 180 km.
Câu 7:
Cho tam giác ABC vuông tại A, đường cao AH, biết AB = 6 cm; AC = 8 cm.
1. Chứng minh: ΔABC đồng dạng ΔHBA. Tính HB; AH.
 Xem đáp án
Xem đáp án
Hướng dẫn giải
1. Áp dụng định lý Py-ta-go vào tam giác ABC vuông tại A có:
Xét hai tam giác ABC và HBA có
Áp dụng định lý Pytago vào tam giác ABH vuông tại H có
Vậy HB = 3,6 cm; AH = 4,8 cm.
Câu 8:
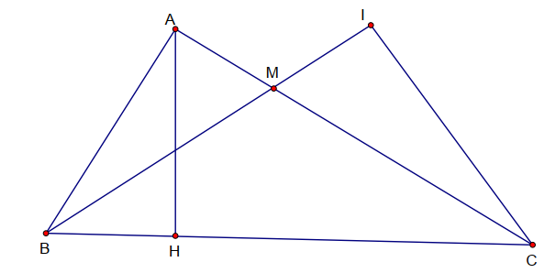
Xác định vị trí điểm M thuộc cạnh AC để diện tích tam giác BIC đạt giá trị lớn nhất.
 Xem đáp án
Xem đáp án
Áp dụng bất đẳng thức Cô-si vào hai cạnh IB và IC ta thấy:
IB2 + IC2 ³ 2IB.IC
Mà áp dụng định lý Py-ta-go vào tam giác BIC vuông tại I nên
BC2 = IB2 + IC2
Thay vào (1) ta suy ra được:
Dấu “=” xảy ra khi và chỉ khi IB = IC.
Suy ra DIBC cân tại I nên tam giác IBC vuông cân tại I
Vậy khi điểm M thuộc AC sao cho thì diện tích tam giác BIC đạt giá trị lớn nhất.
Câu 9:
Lấy điểm M trên cạnh AC (M khác A và C), kẻ CI vuông góc với BM tại I. Chứng minh: MA.MC = MB.MI.
 Xem đáp án
Xem đáp án
2. Xét ∆MAB và ∆MIC có:
(đpcm)
Câu 10:
Cho a1 + a2 + a3 + ... + an = k.
Chứng minh rằng: (n Î ℕ*)
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Áp dụng BĐT Bunhiacopxki vào biểu thức a1 + a2 + a3 + ... + an ta có:
Û k2 £ (a12 + a22 + a32 + ... + an2).n
Vậy suy ra ("n Î ℕ*).
