11 câu hỏi trắc nghiệm thuộc Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 15

Đề kiểm tra cuối kì 2 Toán 8 có đáp án ( Mới nhất)

Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 15

6326 lượt thi
11 câu hỏi
45 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Giải các phương trình:

1) x - 9 = 0

Xem đáp án

Hướng dẫn giải

1) x - 9 = 0

Û x = 9

Vậy tập nghiệm của phương trình là S = {9}.

Câu 2:

Giải các phương trình:

2) (x - 4)(x + 5) = 0

Xem đáp án

2) (x - 4)(x + 5) = 0

$\Leftrightarrow [\begin{matrix} x - 4 = 0 \\ x + 5 = 0 \end{matrix}$

$\Leftrightarrow [\begin{matrix} x = 4 \\ x = - 5 \end{matrix}$

Vậy tập nghiệm của phương trình là S = {-5; 4}.

Câu 3:

Giải các phương trình:

3) $\frac{x + 2}{x - 1} = \frac{x - 3}{x + 1}$

Xem đáp án

3) ĐKXĐ: $\{\begin{matrix} x - 1 \neq 0 \\ x + 1 \neq 0 \end{matrix} \Leftrightarrow \{\begin{matrix} x \neq 1 \\ x \neq - 1 \end{matrix}$

$\frac{x + 2}{x - 1} = \frac{x - 3}{x + 1}$

Þ (x + 2)(x + 1) = (x - 3)(x - 1)

Û x² + 2x + x + 2 = x² - 3x - x + 3

Û 2x + x + 3x + x = 3 - 2

Û 7x = 1

$\Leftrightarrow x = \frac{1}{7}$ (TMĐK)

Vậy tập nghiệm của phương trình là $S = \{\frac{1}{7}\} .$

Câu 4:

1) Cho m > n, chứng tỏ 2 + m > 2 + n.

Xem đáp án

Hướng dẫn giải

1) Ta có: m > n

Cộng hai vế của bất đẳng thức (1) cho 2. Khi đó bất đẳng thức đã cho trở thành:

2 + m > 2 + n (đpcm).

Câu 5:

2) Giải phương trình 2x - 8 < 0 và biểu diễn tập nghiệm trên trục số.

Xem đáp án

2) Ta có: 2x - 8 < 0

Û 2x < 8 Û x < 4

Vậy tập nghiệm của bất phương trình là S = {x | x < 4}.

Khi đó biểu diễn trên trục số của tập nghiệm là:

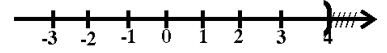
2) Giải phương trình 2x - 8 < 0 và biểu diễn tập nghiệm trên trục số. (ảnh 1)

Câu 6:

Để vận chuyển một số lượng hàng hóa, người ta dự định điều động 15 xe vận tải loại nhỏ, nhưng sau đó tìm được 10 xe vận tải loại lớn nên số hàng hóa mỗi xe chở được thêm 1 tấn. Hỏi số lượng hàng hóa cần vận chuyển là bao nhiêu tấn?

Xem đáp án

Hướng dẫn giải

Gọi x (tấn) là số lượng hàng hóa cần vận chuyển (x > 0)

Ban đầu theo dự định, cần điều động 15 xe vận tải nhỏ thì mỗi xe chở được $\frac{x}{15}$ (tấn)

Lúc sau, khi tìm được 10 xe vận tải loại lớn thì mỗi xe chở được $\frac{x}{10}$ (tấn)

Khi đó, mỗi xe chở được thêm 1 tấn so với dự định ban đầu nên ta có phương trình

$\frac{x}{15} + 1 = \frac{x}{10} \Leftrightarrow \frac{x + 15}{15} = \frac{x}{10}$

$\Leftrightarrow \frac{x + 15}{3} = \frac{x}{2}$

Û 2(x + 15) = 3x

Û 2x + 30 = 3x

Û 3x - 2x = 30

Û x = 30 (TMĐK)

Vậy số lượng hàng hóa cần vận chuyển là 30 tấn.

Câu 7:

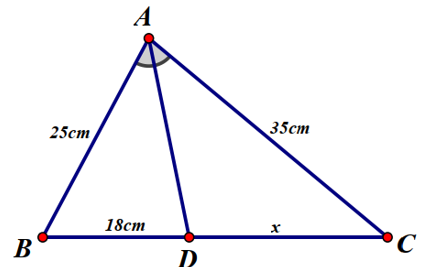
1) Cho tam giác ABC có AD là phân giác trong của góc A. Tìm x trong hình vẽ sau với độ dài cho sẵn trong hình.

Xem đáp án

Hướng dẫn giải

1) Cho tam giác ABC có AD là phân giác trong của góc A. Tìm x trong hình vẽ sau với độ dài cho sẵn trong hình. (ảnh 2)

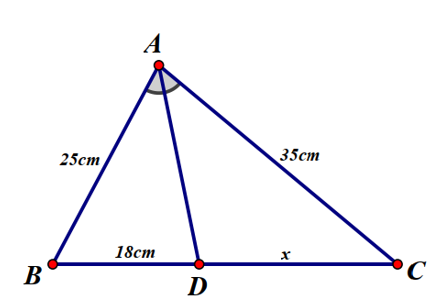
Xét tam giác ABC có AD là đường phân giác của góc A nên theo tính chất đường phân giác trong tam giác, ta có:

$\frac{B D}{A B} = \frac{D C}{A C} \Leftrightarrow \frac{18}{25} = \frac{x}{35}$

$\Leftrightarrow x = 35. \frac{18}{25} = 25,2 (c m) .$

Vậy x = 25,2 cm.

Câu 8:

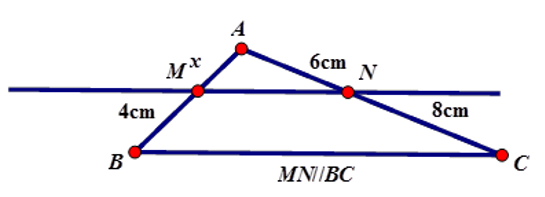
2) Tìm x trong hình vẽ sau với độ dài cho sẵn trong hình. Biết MN// BC.

Xem đáp án

2) Tìm x trong hình vẽ sau với độ dài cho sẵn trong hình. Biết MN// BC. (ảnh 2)

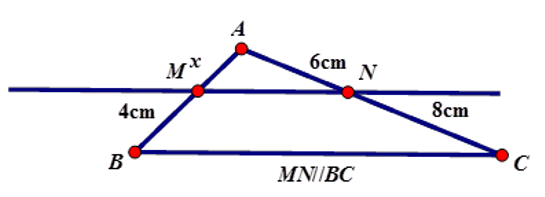
Áp dụng định lý Ta-lét vào tam giác ABC có MN // BC

$\frac{A M}{A B} = \frac{A N}{A C}$ $\Leftrightarrow \frac{A M}{M N} = \frac{A N}{N C}$

$\Leftrightarrow \frac{x}{4} = \frac{6}{8}$ $\Leftrightarrow x = 4. \frac{6}{8} = 3 (c m)$

Vậy x = 3 cm.

Câu 9:

Kim tự tháp là niềm tự hào của người dân Ai Cập. Để tính được chiều cao gần đúng của Kim tự tháp người ta làm như sau, cắm một cây cọc cao 1 m vuông góc với mặt đất và đo được bóng trên mặt đất là 1,5 m và khi đó chiều dài bóng Kim tự tháp trên mặt đất là 208,2 m. Hỏi Kim tự tháp cao bao nhiêu mét? (tạị cùng một thời điểm, các tia nắng mặt trời tạo với mặt đất các góc bằng nhau góc C bằng với góc F).

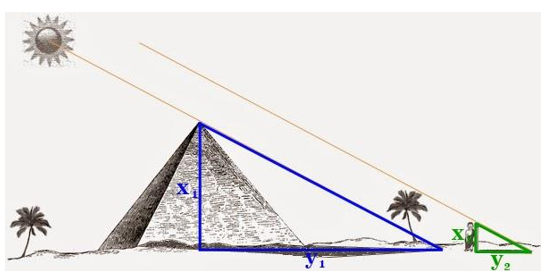
Kim tự tháp là niềm tự hào của người dân Ai Cập. Để tính được chiều cao gần đúng của (ảnh 1)

Xem đáp án

Hướng dẫn giải

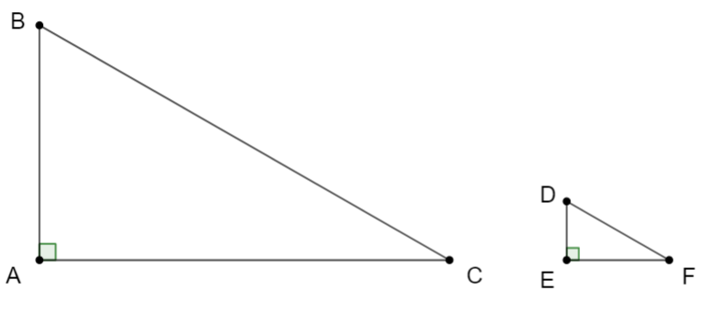
Kim tự tháp là niềm tự hào của người dân Ai Cập. Để tính được chiều cao gần đúng của (ảnh 2)

Xét hai tam giác DABC và DEDF có:

$\begin{matrix} \hat{B A C} = \hat{D E F} (= 90 °) \\ \hat{B C A} = \hat{D F E} (g t) \end{matrix}\} \Rightarrow Δ A B C ∽ Δ E D F (g . g)$

Suy ra $\frac{A B}{E D} = \frac{A C}{E F}$ (các cạnh tương ứng)

$\Leftrightarrow A B = \frac{E D . A C}{E F} = \frac{1.208,2}{1,5} = 138,8 (m) .$

Vậy Kim tự tháp cao 138,8 mét.

Câu 10:

Cho tam giác ABC vuông tại A. Kẻ đường cao AH (H thuộc BC).

1) DABC và DHBA có đồng dạng với nhau không? Vì sao?

Xem đáp án

Hướng dẫn giải

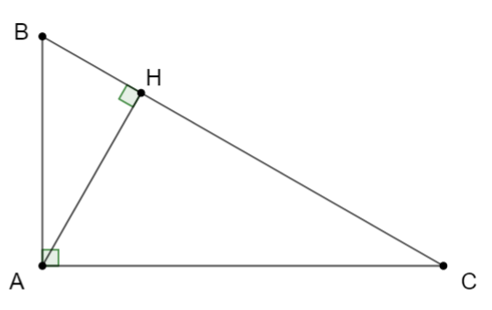
Cho tam giác ABC vuông tại A. Kẻ đường cao AH (H thuộc BC). 1) tam giác ABC và tam giác HBA có đồng dạng với nhau không? Vì sao? (ảnh 1)

1) Xét hai tam giác DABH và DCBA có

$\begin{matrix} \hat{A B H} = \hat{C B A} (\hat{B} c h u n g) \\ \hat{A H B} = \hat{C A B} (= 90 °) \end{matrix}\} \Rightarrow Δ A B H ∽ Δ C B A (g . g)$

Câu 11:

2) Chứng minh: AH² = HB.HC.

Xem đáp án

2) Lần lượt xét hai tam giác vuông ABC và ABH có

+) $\hat{A B C} + \hat{A C B} = 180 ° - \hat{B A C} = 90 °$ (1)

+) $\hat{A B H} + \hat{B A H} = 180 ° - \hat{A H B} = 90 °$ (2)

Từ (1) và (2) nên suy ra $\hat{A C B} = \hat{B A H}$ (vì cùng phụ với góc $\hat{A C B}$ )

Xét hai tam giác DABH và DCAH có

$\begin{matrix} \hat{B A H} = \hat{A C H} (c m t) \\ \hat{A H B} = \hat{C H A} (= 90 °) \end{matrix}\} \Rightarrow Δ A B H ∽ Δ C A H (g . g)$

$\Rightarrow \frac{A H}{C H} = \frac{B H}{A H} \Leftrightarrow A H^{2} = H B . H C$

(đpcm).

Bắt đầu thi ngay

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đề kiểm tra cuối kì 2 Toán 8 có đáp án ( Mới nhất)

Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 15

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương