Giải SBT Toán 6 Chương 3: Hình học trực quan. Các hình phẳng trong thực tiễn - Bộ Chân trời sáng tạo
Bài ôn tập cuối chương 3 - SBT Toán 6 Bộ Chân trời sáng tạo
-
2209 lượt thi
-
14 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Cho hình vuông ABCD có AB = 9 cm. Tính độ dài các đoạn thẳng DC và AD.
 Xem đáp án
Xem đáp án
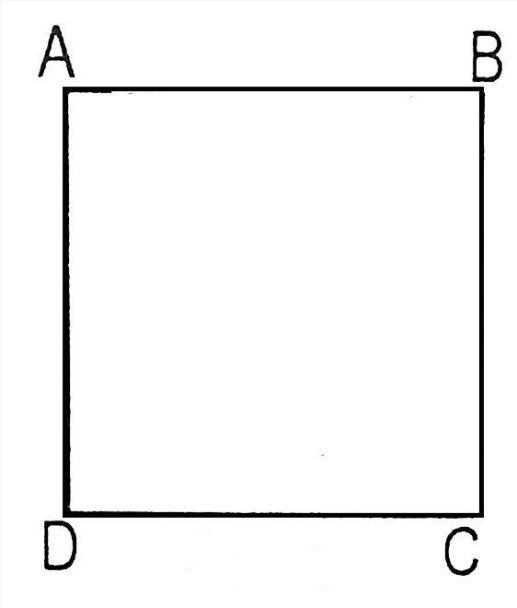
Vì ABCD là hình vuông nên AB = CD = AD = BC = 9 cm.
Vậy AD = CD = 9cm.
Câu 2:
Dùng thước thẳng eke để vẽ hình vuông có độ dài cạnh 7 cm. Hãy dùng compa so sánh hai đường chéo của hình vuông đó
 Xem đáp án
Xem đáp án
- Dùng thước vẽ đoạn thẳng AB = 7 cm:
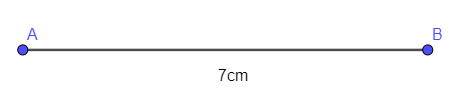
- Dùng eke và thước vẽ các đường thẳng vuông góc với AB tại A và B:
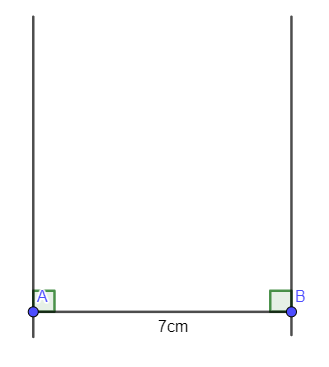
- Trên đường vuông góc tại A lấy điểm D với AD = 7 cm. Trên đường vuông góc tại B lấy điểm C với BC = 7 cm:
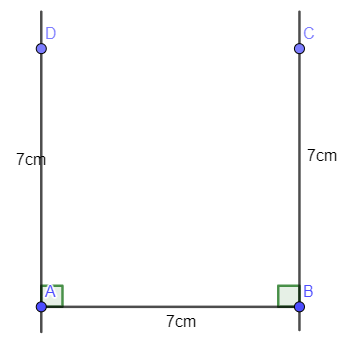
- Kẻ đoạn thẳng nối C và D ta được tứ giác ABCD là hình vuông có độ dài cạnh 7 cm:
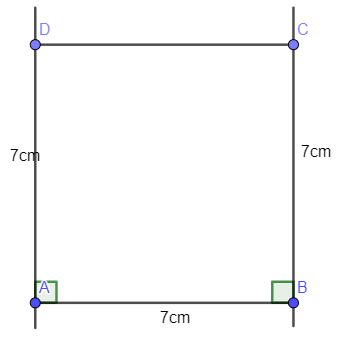
- Sử dụng compa để so sánh hai đường chéo:
Mở compa tâm A bán kính AC vẫn giữ nguyên compa ta đặt một đầu compa vào điểm B và đầu còn lại ta thấy trùng khít với điểm D. Như vậy hai đường chéo của hình vuông bằng nhau.
Câu 3:
Cho tam giác đều DEF có DE = 5 cm. Tính độ dài các cạnh EF, DF.
 Xem đáp án
Xem đáp án
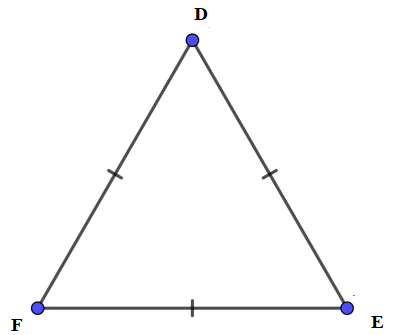
Vì tam giác DEF đều nên DE = EF = DF = 5 cm.
Vậy EF = DF = 5cm.
Câu 4:
Dùng thước và compa để vẽ tam giác đều có độ dài cạnh 3 cm.
 Xem đáp án
Xem đáp án
- Dùng thước vẽ đoạn thẳng AB = 3 cm:
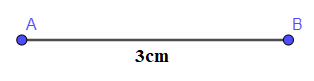
- Dùng compa vẽ các phần đường tròn cùng bán kính 3 cm và có tâm lần lượt là A, B:
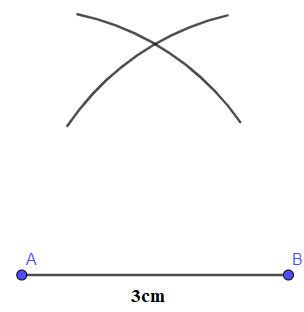
- Hai phần đường tròn nói trên cắt nhau tại điểm C:
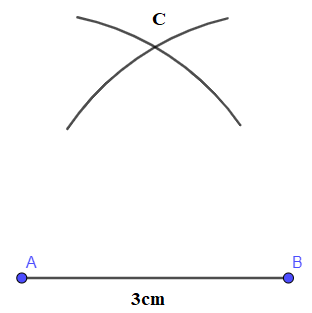
- Kẻ đoạn thẳng nối C và A, C và B ta có tam giác đều ABC với cạnh 3 cm
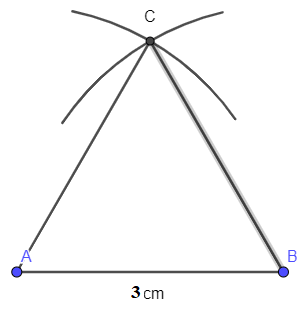
Câu 5:
Cho lục giác đều ABCDEF có cạnh AB = 8 cm và đường chéo AD = 16 cm. Tính độ dài các đoạn thẳng CD và CF
 Xem đáp án
Xem đáp án
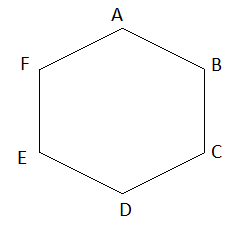
Vì ABCDEF là lục giác đều nên CD = AB = 8 cm; CF = AD = 16 cm.
Vậy CD = 8cm, CF = 16 cm.
Câu 6:
Cho hình chữ nhật ABCD có AB = 12 cm, BC = 9 cm, BD = 15 cm. Tính độ dài của AD, CD, AC.
 Xem đáp án
Xem đáp án

ABCD là hình chữ nhật nên:
AD = BC = 9 cm
CD = AB = 12 cm
AC = BD = 15 cm
Vậy AD = 9cm, CD = 12 cm, AC = 15cm.
Câu 7:
Cho hình thoi ABCD với O là giao điểm của hai đường chéo. Biết AB = 20 cm, OA = 16 cm, OB = 12 cm. Tính độ dài các cạnh và các đường chéo của hình thoi.
 Xem đáp án
Xem đáp án
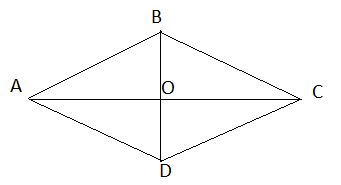
Ta có: ABCD là hình thoi nên:
AD = BC = CD = AB = 20 cm
OA = OC = 16 cm
Suy ra AC = OA + OC = 16 + 16 = 32 cm
OB = OD = 12 cm
Suy ra BD = OB + OD = 12 + 12 = 24 cm
Vậy độ dài cạnh của hình thoi là 20cm và độ dài hai đường chéo lần lượt là 32cm và 24cm.
Câu 8:
Cho hình bình hành ABCD có O là giao điểm của hai đường chéo và thỏa AB = 16 cm, AD = 10 cm, OC = 6 cm. Tính độ dài của CD, BC, AC.
 Xem đáp án
Xem đáp án
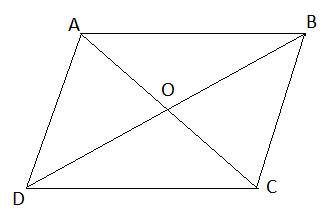
ABCD là hình bình hành nên:
BC = AD = 10 cm
CD = AB = 16 cm
AC = 2.OC = 2.6 = 12 cm
Vậy BC = 10 cm, CD = 16 cm, AC = 12cm.
Câu 9:
Cho hình thang cân MNPQ với cạnh đáy là MN và PQ, PN = 6 cm, PM = 10 cm. Tính MQ, NQ
 Xem đáp án
Xem đáp án
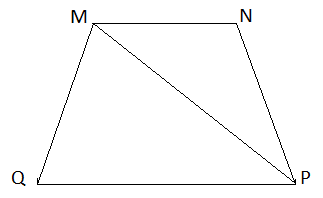
MNPQ là hình thang cân nên:
MQ = NP = 6 cm
NQ = MP = 10 cm
Vậy MQ = 6cm, NQ = 10 cm.
Câu 10:
Tính chu vi và diện tích hình bình hành ABCD (như hình vẽ). Biết rằng AD = 6 cm, AB = 10 cm, DH = 9 cm.
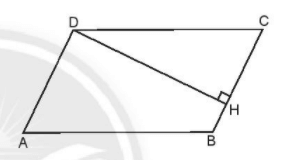
 Xem đáp án
Xem đáp án
Vì ABCD là hình bình hành nên AD = BC = 6cm, AB = CD = 10 cm.
Chu vi hình bình hành là: AB + BC + CD + AD = 6 + 6 + 10 + 10 = 32 (cm)
Diện tích hình bình hành là: BC.DH = 6.9 = 54 (cm2)
Vậy chu vi hình bình hành ABCD là 32cm, diện tích hình bình hành ABCD là 54 cm2.
Câu 11:
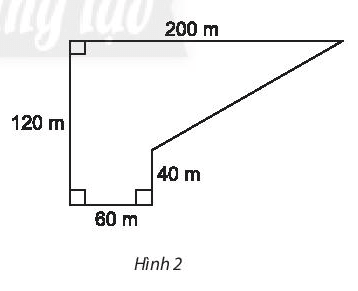
Tính chu vi và diện tích của Hình 1 và tính diện tích của Hình 2 sau đây.
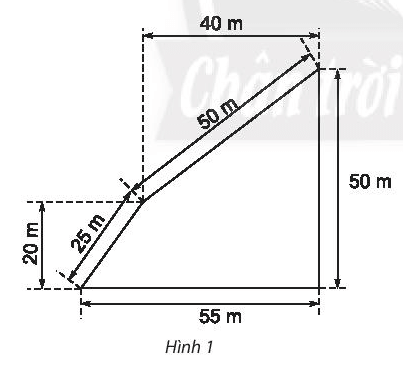
 Xem đáp án
Xem đáp án
Hình 1:
Chu vi hình 1 là: P = 25 + 50 + 50 + 55 = 180 (m)
Để tính diện tích của hình này, ta chia hình này thành các hình như sau:
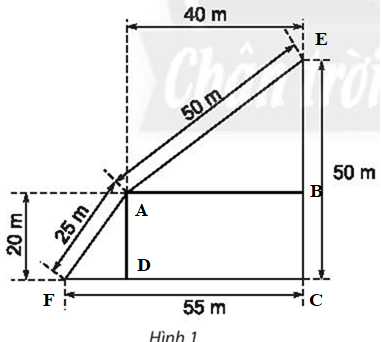
Theo hình vẽ, ta có: AD = BC = 20 m, AB = DC = 40 m, DF = CF – DC = 55 – 40 = 15 m, BE = CE – BC = 50 – 20 = 30 m.
Diện tích hình chữ nhật ABCD là: AB.AD = 40.20 = 800 (m2).
Diện tích tam giác ADF là: AD.DF : 2 = 20.15:2 = 150 (m2).
Diện tích tam giác ABE là: AB.BE : 2 = 40.30: 2 = 600 (m2).
Diện tích của hình đã cho là: 800 + 150 + 600 = 1 550 (m2).
Vậy diện tích của hình đã cho là 1 550 m2.
Hình 2:
Cách 1: Có thể chia hình đã cho thành hình chữ nhật ABCD và hình thang CDEF như sau:
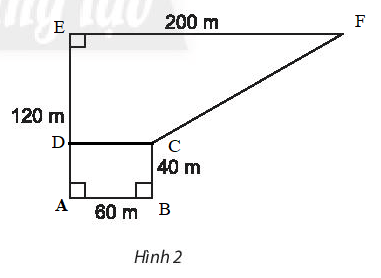
Ta có: AD = BC = 40 m, AB = CD = 60m, DE = AE – AD = 120 – 40 = 80m.
Diện tích hình chữ nhật ABCD là: AB.BC = 60.40 = 2 400 (m2).
Diện tích hình thang CDEF là: (CD + EF).DE:2 = (60 + 200).80:2 = 10 400 (m2).
Diện tích của hình đã cho là: 2 400 + 10 400 = 12 800 (m2).
Vậy chu vi, diện tích của hình đã cho lần lượt là 180 m, 12 800 m2.
Cách 2: Có thể chia hình thành hình chữ nhật MNPQ và hình tam giác PHK như sau:
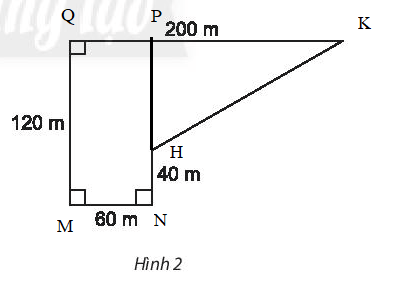
Ta có: PQ = MN = 60 m, PH = PN – NH = 120 – 40 = 80 m, PK = QK – PQ = 200 – 60 = 140 m.
Diện tích hình chữ nhật MNPQ là: MN.MQ = 60. 120 = 7 200 (2).
Diện tích hình tam giác PHK là: PH.PK = 80.140:2 = 5 600 (2).
Diện tích hình đã cho là: 7 200 + 5 600 = 12 800 (2).
Vậy chu vi, diện tích của hình đã cho lần lượt là 180 m và 12 800 2.
Câu 12:
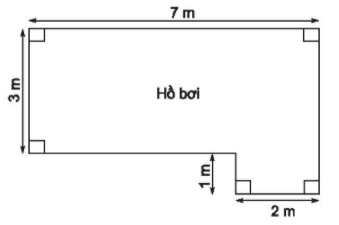
Tính chu vi và diện tích của hồ bơi có kích thước như hình vẽ sau:
 Xem đáp án
Xem đáp án
Chu vi của hồ bơi là:
P = 3 + 7 + 4 + 2 + 1 + 5 = 22 (m)
Ta sẽ chia hình thành các hình nhỏ để dễ dàng tính diện tích:
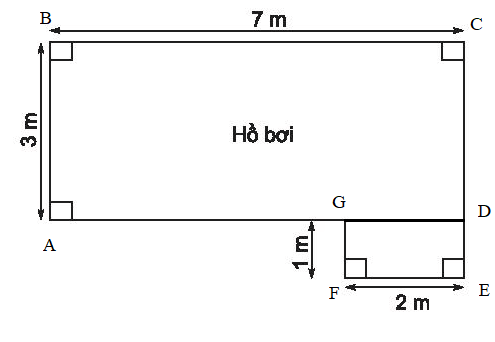
Diện tích của hình chữ nhật ABCD là: AB.BC = 3.7 = 21 (m2).
Diện tích của hình chữ nhật DEFG là: EF.GF = 2.1 = 2 (2).
Diện tích của hình đã cho là: 21 + 2 = 23 (2).
Vậy chu vi của hình đã cho là 22 m và diện tích của hình đã cho là 23 2.
(Có thể chia hình đã cho theo nhiều cách khác nhau để tính toán).
Câu 13:
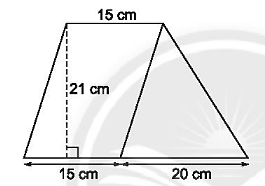
Tính diện tích của hình sau:
 Xem đáp án
Xem đáp án
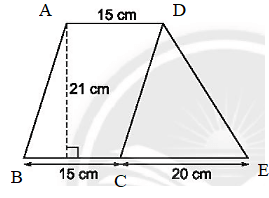
Diện tích hình bình hành ABCD là: 15.21 = 315 (cm2).
Diện tích của tam giác CDE là: 20.21:2 = 210 (cm2).
Diện tích của hình đã cho là: 315 + 210 = 525 (cm2).
Vậy diệc tích của hình đã cho là 525 cm2.
Câu 14:
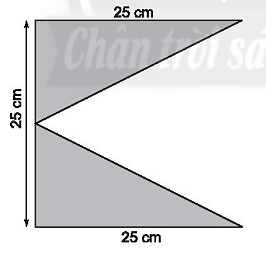
Tính diện tích của hình sau:
 Xem đáp án
Xem đáp án
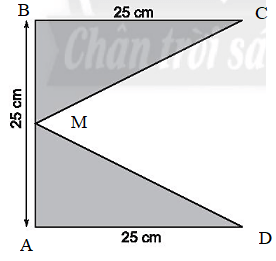
Ta có: AM = BM = 25:2 = 12,5 cm.
Ta nhận thấy diện tích hai tam giác ADM và BCM bằng nhau vì AM = MB, AD = BC nên diện tích của hình đã cho bằng hai lần diện tích tam giác ADM và bằng: 2.(AD.AM:2) = 2.(25.12,5:2) = 25.12,5 = 312,5 (cm2).
Vậy diện tích hình đã cho là 312,5 cm2.
