Trắc nghiệm Chuyên đề Toán 9 Chuyên đề 3: Vị trí tương đối của đường thằng và đường tròn. Vị trí tương đối của hai đường tròn có đáp án
Các dạng bài tập vận dụng - có đáp án
-
853 lượt thi
-
12 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 1:
Cho tam giác ABC vuông tại A, đường cao AH. Gọi M, N lần lượt là điểm đối xứng với H qua AB, AC. E, D là hình chiếu của H lên AB, AC. Chứng minh rằng MN là tiếp tuyến của đường tròn đường kính BC.
 Xem đáp án
Xem đáp án
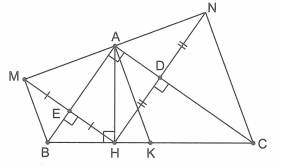
Ta có: .
Tương tự ta có: .
.
thẳng hàng.
Gọi K là trung điểm của BC. Xét tứ giác BMNC có (cùng vuông góc với MN) nên BMNC là hình thang.
Lại có AM = AH =AN (tính chất đối xứng) nên A là trung điểm của MN.
Suy ra KA là đường trung bình của hình thang nên tại A. Do đó MN là tiếp tuyến của đường tròn đường kính BC.
Câu 2:
Cho đường tròn (O) đường kính AB có Ax, By là 2 tia tiếp tuyến của (O) (Ax, By) cùng nằm trên nửa mặt phẳng bờ là đường thẳng AB). Trên tia Ax lấy điểm C sao cho . Chứng minh rằng CD tiếp xúc với đường tròn (O).
 Xem đáp án
Xem đáp án
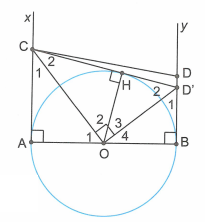
Từ C vẽ tiếp tuyến CD’ của đường tròn (O) (D’ thuộc By) tiếp xúc với (O) tại tiếp điểm H.
Theo tính chất hai tiếp tuyến cắt nhau ta có: OC là phân giác của và OD’ là phân giác của .
Mà hai góc và là hai góc kề bù nên .
Mà theo giả thiết và D, D’ đều thuộc By nên suy ra D’ = D.
Vì CD’ là tiếp tuyến của (O) nên CD cũng là tiếp tuyến của (O).
Câu 3:
Cho đường tròn (O; R) đường kính AB. Vẽ dây AC sao cho . Trên tia đối của tia BA, lấy điểm M sao cho B là trung điểm của OM. Chứng minh rằng:
a) MC là tiếp tuyến của đường tròn (O).
b) .
 Xem đáp án
Xem đáp án
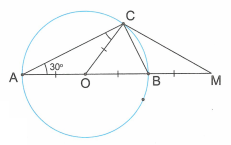
a) Ta có: (góc ngoài của ).
Suy ra là tam giác đều.
vuông tại C hay .
Vậy MC là tiếp tuyến của đường tròn (O).
b) Áp dụng định lí Pytago trong tam giác vuông OMC có:
.
Câu 4:
Cho tam giác ABC vuông tại A có AB = 8, AC = 15. Vẽ đường cao AH. Gọi D là điểm đối xứng với B qua H. Vẽ đường tròn đường kính CD, cắt AC ở E.
a) Chứng minh rằng HE là tiếp tuyến của đường tròn.
b) Tính độ dài HE.
 Xem đáp án
Xem đáp án
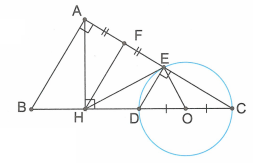
a) Gọi O là trung điểm của CD.
Vì tam giác DEC có một cạnh DC là đường kính của đường tròn (O) nên .
Kẻ
cân tại H (hai góc đáy).
Mà (vì cùng phụ với ).
Suy ra . (1)
Mặt khác ta cũng có (do cân tại O). (2)
Từ (1) và (2) ta có
hay HK là tiếp tuyến của (O).
b) Áp dụng định lí Pytago trong tam giác vuông ABC ta được:
.
Áp dụng hệ thức lượng trong tam giác vuông ABC ta được:
.
Do cân tại H nên .
Câu 5:
Từ một điểm M ở ngoài đường tròn (O), vẽ hai tiếp tuyến MA, MB với đường tròn. Trên tia OB lấy điểm C sao cho BC = BO. Chứng minh rằng .
 Xem đáp án
Xem đáp án
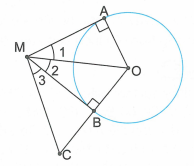
Ta có: (tính chất hai tiếp tuyến cắt nhau).
(do cân tại M).
,
,
Câu 6:
Từ một điểm A ở ngoài đường tròn (O; R), vẽ hai tiếp tuyến AB, AC với đường tròn. Đường thẳng vuông góc với OB tại O cắt AC tại N. Đường thẳng vuông góc với OC tại O cắt AB tại M.
a) Chứng minh rằng tứ giác AMON là hình thoi.
b) Điểm A phải cách điểm O một khoảng bao nhiêu để cho MN là tiếp tuyến của (O).
 Xem đáp án
Xem đáp án
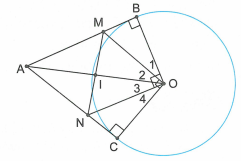
a) Dễ thấy và nên AMON là hình bình hành.
Ta có: .
.
Vậy AMON là hình thoi.
b) Gọi I là giao điểm của AO và MN. Vì AMON là hình thoi nên I trung điểm của OA và .
Do đó MN là tiếp tuyến của (O) thuộc đường tròn (O) .
Câu 7:
Cho đường tròn (O;R) và một điểm A cố định trên đường tròn đó. Qua A vẽ tiếp tuyến xy. Từ một điểm M trên xy vẽ tiếp tuyến MB với đường tròn (O). Hai đường cao AD và BE của tam giác MAB cắt nhau tại H.
a) Chứng minh rằng ba điểm M, H, O thẳng hàng.
b) Chứng minh rằng tứ giác AOBH là hình thoi.
c) Khi điểm M di động trên xy thì điểm H di động trên đường nào?
 Xem đáp án
Xem đáp án
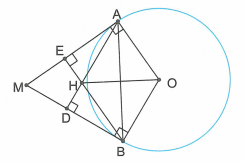
a) H là trực tâm của tam giác AMB nên .
Mà (tính chất hai tiếp tuyến cắt nhau) nên ba điểm M, H, O thẳng hàng.
b) ABOH là hình bình hành vì có .
Lại có nên AOBH là hình thoi.
c) Vì AOBH là hình thoi nên (không đổi) và A cố định nên khi M di động trên xy thì điểm H di động trên đường tròn (A; R).
Câu 8:
Cho tam giác đều ABC, O là trung điểm của BC. Trên các cạnh AB, AC lần lượt lấy các điểm di động D, E sao cho .
a) Chứng minh rằng BD.CE không đổi.
b) Chứng minh . Từ đó suy ra tia DO là tia phân giác của góc BDE.
c) Vẽ đường tròn tâm O tiếp xúc với AB. Chứng minh rằng đường tròn này luôn tiếp xúc với DE.
 Xem đáp án
Xem đáp án
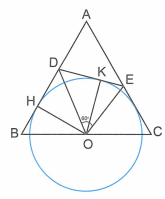
a) là góc ngoài của tam giác BOD nên . (1)
Mà (2)
Từ (1) và (2) suy ra .
Do đó (không đổi).
b) (vì OB = OC).
Do đó .
c) Giả sử AB tiếp xúc với (O) tại H, kẻ .
Xét và có:
OD chung
(chứng minh trên)
(cạnh huyền – góc nhọn) .
Vậy đường tròn (O) luôn tiếp xúc với DE.
Câu 9:
Cho hai đường tròn (O) và (O’) tiếp xúc ngoài với nhau tại B. Vẽ đường kính AB của đường tròn (O) và đường kính BC của đường tròn (O’). Đường tròn đường kính OC cắt (O) tại M và N.
a) Đường thẳng CM cắt (O’) tại P. Chứng minh: .
b) Từ C vẽ đường thẳng vuông góc với CM cắt tia ON tại D. Chứng minh tam giác OCD là tam giác cân.
 Xem đáp án
Xem đáp án
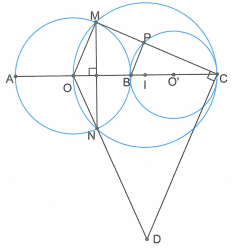
a) Dễ thấy hai tam giác BPC và OMC lần lượt vuông tại P và M. Do đó .
b) Gọi I là trung điểm của OC. Ta thấy đường tròn (O) và (I) cắt nhau tại hai điểm M và N nên .
Mà cân tại O (vì OM= ON) nên OI cũng là tia phân giác của góc . (1)
Mặt khác (cùng vuông góc với MC).
(so le trong). (2)
Từ (1) và (2) suy ra cân tại D.
Câu 10:
Cho hai đường tròn (O;R) và (O’; R’) cắt nhau tại A và B sao cho đường thẳng OA là đường tiếp tuyến của đường tròn (O’; R’). Biết OA =12cm, O’A = 5cm.
a) Chứng minh O’A là tiếp tuyến của đường tròn (O;R).
b) Tính độ dài các đoạn thẳng OO’, AB.
 Xem đáp án
Xem đáp án
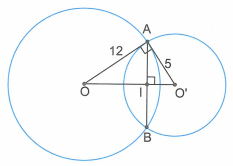
a) Vì OA là tiếp tuyến của đường tròn (O’;R’) nên cũng là tiếp tuyến của đường tròn (O; R).
b) Áp dụng định lí Pytago trong tam giác vuông OAO’ ta tính được OO’ = 13cm.
Áp dụng hệ thức lượng trong tam giác vuông OAO’, ta có:
.
Theo tính chất của hai đường tròn cắt nhau, ta có OO’ là trung trực của đoạn thẳng AB.
.Câu 11:
Cho hai đường tròn đồng tâm (O; R) và (O; r). Dây AB của (O; R) tiếp xúc với (O; r). Trên tia AB lấy điểm E sao cho B là trung điểm của đoạn AE. Từ E vẽ tiếp tuyến thứ hai của (O; r) cắt (O; R) tại C và D (D ở giữa E và C).
a) Chứng minh EA = EC.
b) Chứng minh EO vuông góc với BD.
c) Điểm E chạy trên đường nào khi dây AB của (O; R) thay đổi nhưng luôn tiếp xúc với (O; r)?
 Xem đáp án
Xem đáp án
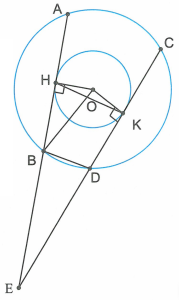
a) Kẻ .
Ta có OH = OK (bán kính đường tròn (O; r) nên AB = CD (liên hệ khoảng cách từ tâm đến dây).
Mà (quan hệ đường kính và dây cung)
Nên . (1)
EH và EK là hai tiếp tuyến của đường tròn (O; r) nên theo tính chất của hai tiếp tuyến cắt nhau ta có: HE = EK. (2)
Từ (1) và (2) ta có: (đpcm).
b) Dễ thấy .
Mà (tính chất hai tiếp tuyến cắt nhau) nên .
c) Ta có OH = r, OB = R. Ta tính được .
.
(không đổi).
Do O cố định nên E luôn chạy trên đường tròn .
Câu 12:
Cho đường tròn (O; R) và đường thẳng d cố định không cắt đường tròn. Từ một điểm A bất kỳ trên đường thẳng d kẻ tiếp tuyến AB với đường tròn (B là tiếp điểm). Từ B kẻ đường thẳng vuông góc với AO tại H, trên tia đối của tia HB lấy điểm C sao cho H là trung điểm của BC.
a) Chứng minh C thuộc đường tròn (O; R) và AC là tiếp tuyến của đường tròn (O; R).
b) Từ O kẻ đường thẳng vuông góc với đường thẳng d tại I, OI cắt BC tại K.
Chứng minh .
c) Chứng minh khi A thay đổi trên đường thẳng d thì đường thẳng BC luôn đi qua một điểm cố định.
 Xem đáp án
Xem đáp án
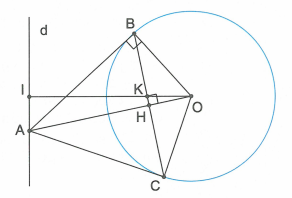
a)
thuộc đường tròn (O; R).
. Vậy AC là tiếp tuyến của (O; R).
b) Ta có:
.
vuông tại B có nên
.
Do đó .
c) Theo câu b) ta có: không đổi.
Mà K thuộc OI cố định nên K cố định.
Vậy khi A thay đổi trên đường thẳng d thì đường thẳng BC luôn đi qua điểm K cố định.
