Trắc nghiệm Hình cầu. Diện tích mặt cầu và thể tích hình cầu có đáp án (Vận dụng)
Trắc nghiệm Hình cầu. Diện tích mặt cầu và thể tích hình cầu có đáp án (Vận dụng)
-
559 lượt thi
-
12 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Cho hình chữ nhật ABCD có AB = 4cm; AD = 3cm. Tính diện tích mặt cầu thu được khi quay nửa đường tròn ngoại tiếp hình chữ nhật ABCD quay quanh đường thẳng MN với M là trung điểm AD, N là trung điểm BC.
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: A
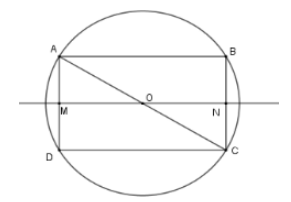
Gọi O là tâm của hình chữ nhật nên OA = OB = OC = OD nên O là tâm đường tròn ngoại tiếp hình chữ nhật ABCD. Khi đó bán kính đường tròn là R = OA =
Theo định lý Pytago ta có:
Khi quay nửa đường tròn ngoại tiếp hình chữ nhật ABCD quay quanh đường thẳng MN với M là trung điểm AD, N là trung điểm BC ta được một hình cầu tâm O bán kính R =
Diện tích mặt cầu là .
Chú ý: Một số em có thể nhớ nhầm công thức diện tích thành S = R2 dẫn đến ra kết quả D sai.
Câu 2:
Cho hình chữ nhật ABCD có AB = 8cm; AD = 6cm. Tính diện tích mặt cầu thu được khi quay nửa đường tròn ngoại tiếp hình chữ nhật ABCD quay quanh đường thẳng MN với M là trung điểm AD, N là trung điểm BC.
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: B.
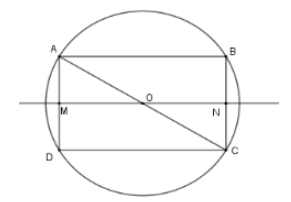
Gọi O là tâm của hình chữ nhật nên OA = OB = OC = OD nên O là tâm đường tròn ngoại tiếp hình chữ nhật ABCD. Khi đó bán kính đường tròn là R = OA =
Theo định lý Pytago ta có:
Khi quay nửa đường tròn ngoại tiếp hình chữ nhật ABCD quay quanh đường thẳng MN với M là trung điểm AD, N là trung điểm BC ta được một hình cầu tâm O bán kính R = 5cm
Diện tích mặt cầu là .
Chú ý: Một số em có thể nhớ nhầm công thức diện tích thành S = R2 dẫn đến ra kết quả D sai.
Câu 3:
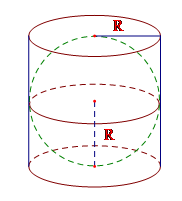
Cho một hình cầu và hình trụ ngoại tiếp nó (đường kính đáy và chiều cao của hình trụ bằng nhau và bằng đường kính của hình cầu). Tính tỉ số giữa diện tích mặt cầu và diện tích xung quanh của hình trụ.
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: B.
Vì đường kính đáy và chiều cao của hình trụ bằng nhau và bằng đường kính hình cầu nên h = 2R với R là bán kính hình cầu và cũng là bán kính đáy của hình trụ
Diện tích mặt cầu
Diện tích xung quanh của hình trụ là: .
Tỉ số giữa diện tích mặt cầu và diện tích xung quanh của hình trụ là:
Chú ý: Một số em có thể tính nhầm mối quan hệ giữa đường cao với bán kính của hình trụ h = R dẫn đến ra kết quả sai là D.
Câu 4:
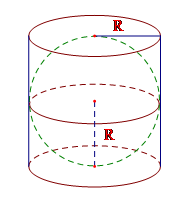
Cho một hình cầu và hình trụ ngoại tiếp nó (đường kính đáy và chiều cao của hình trụ bằng nhau và bằng đường kính của hình cầu). Tính tỉ số giữa diện tích mặt cầu và diện tích toàn phần của hình trụ.
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: C.
Vì đường kính đáy và chiều cao của hình trụ bằng nhau và bằng đường kính hình cầu nên h = 2R với R là bán kính hình cầu và cũng là bán kính đáy của hình trụ
Diện tích mặt cầu .
Diện tích toàn phần của hình trụ là:
Tỉ số giữa diện tích mặt cầu và diện tích xung quanh của hình trụ là:
.
Câu 5:
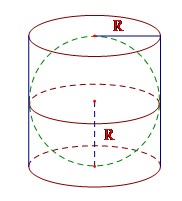
Cho một hình cầu nội tiếp trong hình trụ. Biết rằng đường kính đáy và chiều cao của hình trụ bằng nhau và bằng đường kính của hình cầu. Tính tỉ số giữa thể tích hình cầu và thể tích hình trụ.
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: A
Vì đường kính đáy và chiều cao của hình trụ bằng nhau và bằng đường kính hình cầu nên h = 2R với R là bán kính hình cầu và cũng là bán kính đáy của hình trụ
Thể tích hình cầu ;
Thể tích khối trụ
Tỉ số thể tích hình cầu và thể tích hình trụ là
.
Chú ý: Một số em có thể tính nhầm thành tỉ số giữa thể tích khối trụ và thể tích khối cầu dẫn đến ra đáp án sai là B.
Câu 6:
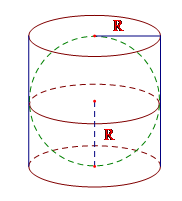
Cho một hình cầu nội tiếp trong hình trụ. Biết rằng chiều cao của hình trụ bằng ba lần bán kính đáy bà bán kính đáy hình trụ bằng bán kính của hình cầu. Tính tỉ số giữa thể tích hình cầu và thể tích hình trụ.
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: B.
Từ đề bài suy ra chiều cao của hình trụ là h = 3R với R là bán kính hình cầu và cũng là bán kính đáy của hình trụ
Thể tích hình cầu ;
Thể tích khối trụ .
Tỉ số thể tích hình cầu và thể tích hình trụ là
.
Chú ý: Một số em có thể tính nhầm thành tỉ số giữa thể tích khối trụ và thể tích khối cầu dẫn đến ra đáp án sai là C.
Câu 7:
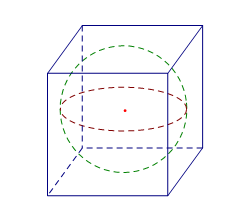
Cho một hình cầu và một hình lập phương ngoại tiếp nó. Tính tỉ số giữa diện tích mặt cầu và diện tích toàn phần của hình lập phương.
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: C
Vì hình cầu nội tiếp hình lập phương nên bán kính hình cầu R = với a là cạnh hình lập phương
Khi đó ta có diện tích mặt cầu
Diện tích toàn phần của hình lập phương
Tỉ số giữa diện tích mặt cầu và diện tích toàn phần của hình lập phương là
Chú ý: Một số em có thể quên mất số trong khi tính diện tích mặt cầu nên ra tỉ số sai là dẫn đến chọn đáp án B sai.
Câu 8:
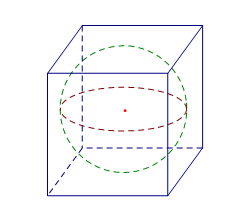
Cho một hình cầu và một hình lập phương ngoại tiếp nó.Nếu diện tích toàn phần của hình lập phương là thì diện tích mặt cầu là:
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: A
Vì hình cầu nội tiếp hình lập phương nên bán kính hình cầu R = với a là cạnh hình lập phương
Diện tích toàn phần của hình lập phương
Suy ra R = = 1cm
Khi đó ta có diện tích mặt cầu .
Chú ý: Một số em có thể quên mất số 4 trong khi tính diện tích mặt cầu nên chọn đáp án B sai.
Câu 9:
Cho tam giác ABC vuông cân tại A có cạnh góc vuông bằng a. Tính diện tích mặt cầu được tạo thành khi quay nửa đường tròn ngoại tiếp tam giác ABC một vòng quanh cạnh BC.
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: A.
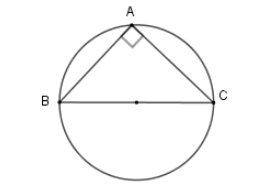
Vì tam giác ABC vuông tại A nên có đường tròn ngoại tiếp là đường tròn đường kính BC
Bán kính đường tròn ngoại tiếp tam giác là R = .
Theo định lý Pytago ta có
Khi quay nửa đường tròn ngoại tiếp tam giác ABC một vòng quanh cạnh BC ta được hình cầu có bán kính nên diện tích mặt cầu là
Chú ý: Một số em có thể sử dụng sai công thức diện tích mặt cầu nên chọn đáp án B sai.
Câu 10:
Cho tam giác ABC vuông cân tại A có cạnh góc vuông bằng 6cm. Tính diện tích mặt cầu được tạo thành khi quay nửa đường tròn ngoại tiếp tam giác ABC một vòng quanh cạnh BC.
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: A.
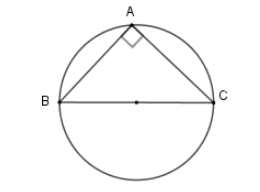
Vì tam giác ABC vuông tại A nên có đường tròn ngoại tiếp là đường tròn đường kính BC
Bán kính đường tròn ngoại tiếp tam giác là R = .
Theo định lý Pytago ta có
.
Khi quay nửa đường tròn ngoại tiếp tam giác ABC một vòng quanh cạnh BC ta được hình cầu có bán kính nên diện tích mặt cầu là
.
Chú ý: Một số em có thể sử dụng sai công thức diện tích mặt cầu nên chọn đáp án B sai.
Câu 11:
Cho một tam giác đều ABC có cạnh AB = 8cm, đường cao AH. Khi đó thể tích hình cầu được tạo thành khi quay nửa đường tròn nội tiếp tam giác ABC một vòng quanh AH.
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: C.
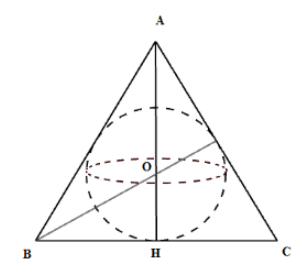
Vì ABC là tam giác đều nên tâm đường tròn nội tiếp trùng với trọng tâm O của tam giác
Khi đó bán kính đường tròn nội tiếp R = OH =
Xét tam giác vuông ABH có:
Suy ra R = .
Khi quay nửa đường tròn nội tiếp tam giác ABC một vòng quanh AH ta được hình cầu bán kính R = V =
Chú ý: Một số em có thể nhớ sai công thức thể tích hình cầu thành dẫn đến tính toán ra đáp án B sai.
Câu 12:
Cho một tam giác đều ABC có cạnh AB = 12cm, đường cao AH. Khi đó thể tích hình cầu được tạo thành khi quay nửa đường tròn nội tiếp tam giác ABC một vòng quanh AH.
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: D.
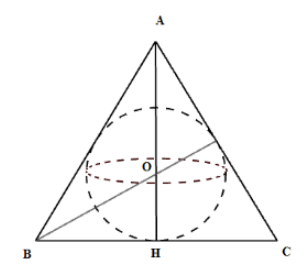
Vì ABC là tam giác đều nên tâm đường tròn nội tiếp trùng với trọng tâm O của tam giác
Khi đó bán kính đường tròn nội tiếp R = OH =
Xét tam giác vuông ABH có: .
.
Suy ra R = .
Khi quay nửa đường tròn nội tiếp tam giác ABC một vòng quanh AH ta được hình cầu bán kính .
Chú ý: Một số em có thể nhớ sai công thức thể tích hình cầu thành dẫn đến tính toán ra đáp án C sai.
