12 câu hỏi trắc nghiệm thuộc Trắc nghiệm Liên hệ giữa cung và dây có đáp án (Vận dụng)

Câu 1:

Cho đường tròn (O) có hai dây AB, CD song song với nhau. Kết luận nào sau đây là đúng?

A. AD > BC

B. Số đo cung AD bằng số đo cung BC

C. AD < BC

D. $\hat{A O D} > \hat{C O B}$

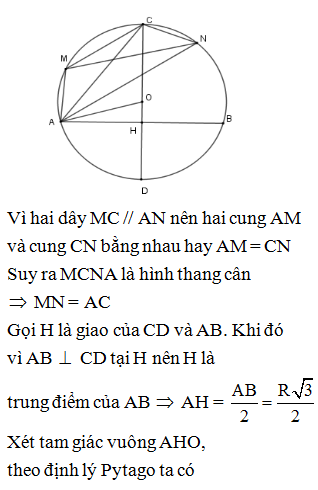
Chú ý: Lời giải trên chính là một cách chứng minh cho tính chất “Trong một đường tròn, hai cung bị chắn giữa hai dây song song thì bằng nhau”.

Câu 2:

Cho đường tròn (O) có hai dây AB, CD song song với nhau. Kết luận nào sau đây là sai?

A. AD = BC

B. Số đo cung AD bằng số đo cung BC

C. BD > AC

D. $\hat{A O D} = \hat{C O B}$

Xem đáp án

Câu 3:

Cho đường tròn (O) đường kính AB và một dây cung AC có số đo nhỏ hơn 90^o. Vẽ dây CD vuông góc với AB và dây DE song song với AB. Chọn kết luận sai?

A. AC = BE

B. Số đo cung AD bằng số đo cung BE

C. Số đo cung AC bằng số đo cung BE

D. $\hat{A O C} < \hat{A O D}$

Xem đáp án

Câu 4:

Cho đường tròn (O) đường kính AB và một cung AC có số đo bằng 50^o. Vẽ dây CD vuông góc với AB và dây DE song song với AB. Chọn kết luận sai?

A. AD = DE = BE

B. Số đo cung AE bằng số đo cung BD

C. Số đo cung AC bằng số đo cung BE

D. $\hat{A O C} = \hat{A O D} = \hat{B O E} = 50^{o}$

Xem đáp án

Câu 5:

Cho tam giác ABC có $\hat{B}$ = 60^o, đường trung tuyến AM, đường cao CH. Vẽ đường tròn ngoại tiếp BHM. Kết luận nào đúng khi nói về các cung HB; MB; MH của đường tròn ngoại tiếp tam giác MHB?

A. Cung HB nhỏ nhất

B. Cung MB lớn nhất

C. Cung MH nhỏ nhất

D. Ba cung bằng nhau

Xem đáp án

Câu 6:

Cho tam giác ABC có $∠ B$ = 30^o, đường trung tuyến AM, đường cao CH. Vẽ đường tròn ngoại tiếp BHM. Kết luận nào sai khi nói về các cung HB; MB; MH của đường tròn ngoại tiếp tam giác MHB?

A. Cung HB lớn nhất

B. Cung HB nhỏ nhất

C. Cung MH nhỏ nhất

D. Cung MB = cung MH

Xem đáp án

Câu 7:

Cho đường tròn (O; R), dây cung AB = R $\sqrt{3}$ . Vẽ đường kính CD AB (C thuộc cung lớn AB). Trên cung AC nhỏ lấy điểm M, vẽ dây AN // CM. Độ dài đoạn MN là:

A. MN = R $\sqrt{3}$

B. MN = R $\sqrt{2}$

C. MN = $\frac{3 R}{2}$

D. MN = $\frac{R \sqrt{5}}{2}$

Xem đáp án

Câu 8:

Cho đường tròn (O; R), dây cung AB = R $\sqrt{2}$ . Vẽ đường kính CD $⊥$ AB (C thuộc cung lớn AB). Trên cung AC nhỏ lấy điểm M, vẽ dây AN // CM. Độ dài đoạn MN là:

A. MN = R $\sqrt{3}$

B. MN = R $\sqrt{2}$

C. MN = $(2 + \sqrt{2})$ R

D. MN = R $\sqrt{2 + \sqrt{2}}$

Xem đáp án

Câu 9:

Cho đường tròn (O; R) có hai dây cung AB và CD vuông góc với nhau tại I (C thuộc cung nhỏ AB). Kẻ đường kính BE của (O). Đẳng thức nào sau đây là đúng?

A. IA² + IC² + IB² + ID² = 2R².

B. IA² + IC² + IB² + ID² = 3R².

C. IA² + IC² + IB² + ID² = 4R²

D. IA² + IC² + IB² + ID² = 5R²

Xem đáp án

Câu 10:

Cho đường tròn (O; R) có hai dây cung AB và CD vuông góc với nhau tại I (C thuộc cung nhỏ AB). Kẻ đường kính BE của (O). Đẳng thức nào sau đây là sai?

A. IA² + IC² + IB² + ID² = AD²+ BC²

B. IA² + IC² + IB² + ID² = BD²+ AC²

C. IA² + IC² + IB² + ID² = BE²

D. IA² + IC² + IB² + ID² = AD²

Xem đáp án

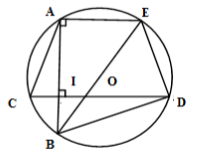
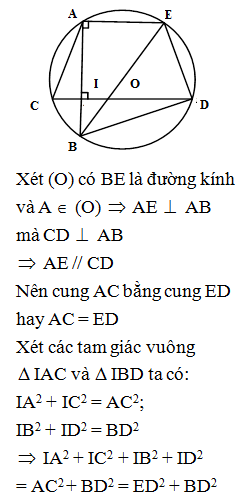
Xét (O) có BE là đường kính và A (O) AE AB mà CD $⊥$ AB

AE // CD

Nên cung AC bằng cung ED hay AC = ED

Xét các tam giác vuông IAC và IBD ta có:

IA² + IC² = AC²; IB² + ID² = BD²

IA² + IC² + IB² + ID² = AC²+ BD² = ED² + BD²

Mà $∆$ BED vuông tại D nên ED² + BD²= EB²

Hay IA² + IC² + IB² + ID² = BE² nên C đúng mà BE AD nên D sai

Xét các tam giác vuông IAD và IBC ta có:

IA² + ID² = AD²; IB² + IC² = BC² IA² + IC² + IB² + ID² = AD²+ BC²

Vậy A, B, C đúng, D sai

Đáp án cần chọn là: D

Câu 11:

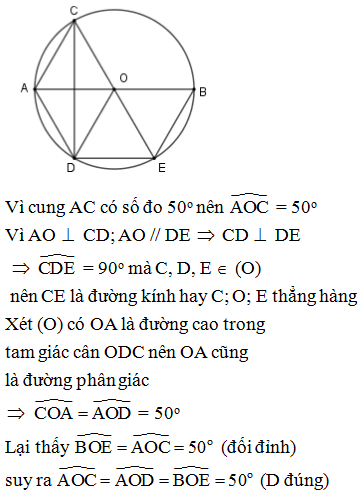
Cho đường tròn (O) đường kính AB và đường tròn (O’) đường kính AO. Các điểm C, D thuộc đường tròn (O) sao cho B cung CD và cung BC nhơ bằng cung BD nhỏ. Các dây cung AC và AD cắt đường tròn (O’) theo thứ tự E và F. So sánh cung OE và cung OF của đường tròn (O’)

A. Cung OE > cung OF

B. Cung OE < cung OF

C. Cung OE = cung OF

D. Chưa đủ điều kiện so sánh

Xem đáp án

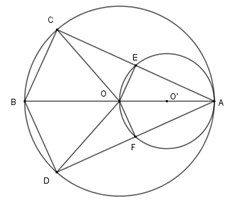
Xét (O’) với OA là đường kính và E (O’) nên OE $⊥$ AC

Tương tự với (O) ta có BC $⊥$ AC nên OE // BC mà O là trung điểm của AB

E là trung điểm của AC OE = $\frac{1}{2}$ BC

Tương tự OF = $\frac{1}{2}$ DB mà cung BC bằng cung BD nên BC = BD => OE = OF hay cung OE = cung OF

Đáp án cần chọn là: C

Câu 12:

Cho đường tròn (O) có hai dây AB, CD song song với nhau. Kết luận nào sau đây là đúng?

A. AD > BC

B. Số đo cung AD bằng số đo cung BC

C. AD < BC

D. $\hat{AOD} = \hat{COB}$

Xem đáp án

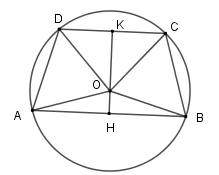
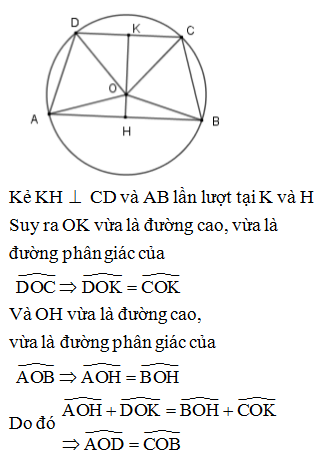
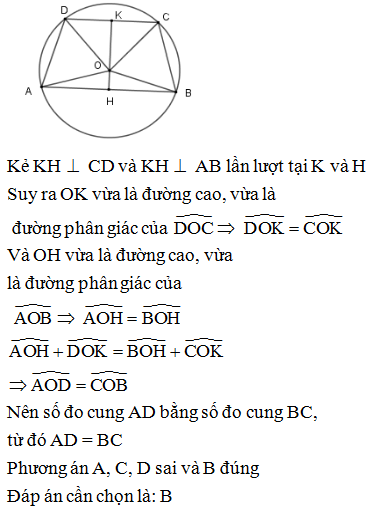
Kẻ KH $⊥$ CD và KH $⊥$ AB lần lượt tại K và H

Suy ra OK vừa là đường cao, vừa là đường phân giác của

$\hat{D O C} \Rightarrow \hat{D O K} = \hat{C O K}$

Và OH vừa là đường cao, vừa là đường phân giác của

$\hat{A O B} \Rightarrow \hat{A O H} = \hat{B O H}$

$\begin{array}{l} \hat{A O H} + \hat{D O K} \\ = \hat{B O H} + \hat{C O K} \Rightarrow \hat{A O D} = \hat{C O B} \end{array}$

Nên số đo cung AD bằng số đo cung BC, từ đó AD = BC

Phương án A, C, D sai, B đúng

Đáp án cần chọn là: B

Lưu ý: Lời giải trên chính là một cách chứng minh cho tính chất “Trong một đường tròn, hai cung bị chắn giữa hai dây song song thì bằng nhau”

CHỌN BỘ SÁCH BẠN MUỐN XEM

Trắc nghiệm Liên hệ giữa cung và dây có đáp án

Trắc nghiệm Liên hệ giữa cung và dây có đáp án (Vận dụng)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương