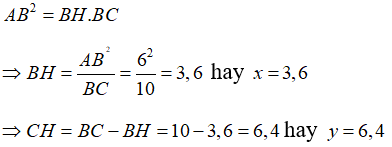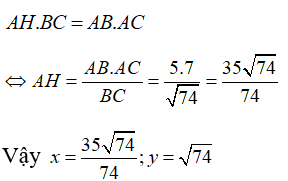10 câu hỏi trắc nghiệm thuộc Bài 1 (có đáp án): Một số hệ thức về cạnh và đường cao trong tam giác vuông

Bài 1 (có đáp án): Một số hệ thức về cạnh và đường cao trong tam giác vuông

Đề số 1

Bài 1 (có đáp án): Một số hệ thức về cạnh và đường cao trong tam giác vuông

712 lượt thi
10 câu hỏi
30 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

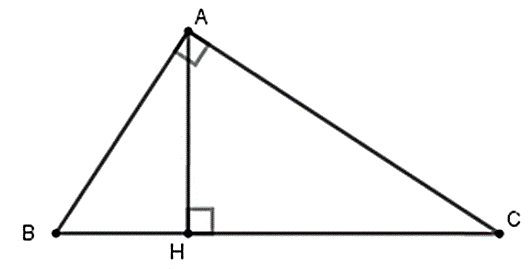
Câu 1:

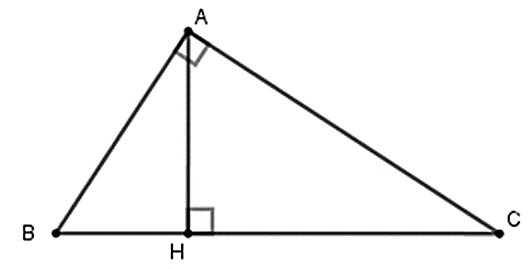
Cho tam giác ABC vuông tại A , đường cao AH (như hình vẽ). Hệ thức nào sau đây là đúng?

A. $A H^{2}$ = AB.AC

B. $A H^{2}$ = BH.CH

C. $A H^{2}$ = AB.BH

D. $A H^{2}$ = CH.BC

Xem đáp án

Đáp án B

Cho tam giác ABC vuông tại A , đường cao AH. Khi đó ta có hệ thức: $A H^{2}$ = BH.CH

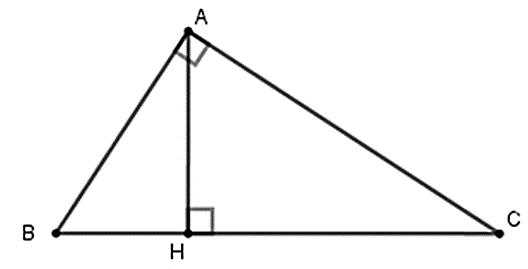
Câu 2:

Cho tam giác ABC vuông tại A , đường cao AH (như hình vẽ). Hệ thức nào sau đây là sai?

A. $A B^{2} = B H . B C$

B. $A C^{2} = C H . B C$

C. AB.AC = AH.BC

D. $A H^{2} = \frac{A B^{2} + A C^{2}}{A B^{2} . A C^{2}}$

Xem đáp án

Đáp án D

Cho tam giác ABC vuông tại A , đường cao AH. Khi đó ta có các hệ thức:

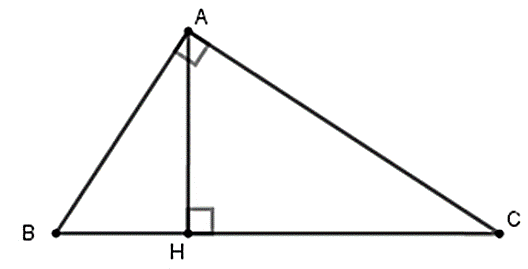
Câu 3:

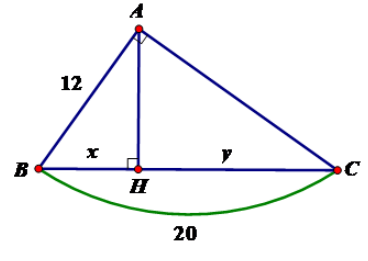
Tính x, y trong hình vẽ sau:

A. x = 7,2; y = 11,8

B. x = 7; y = 12

C. x = 7,2; y = 12,8

D. x = 7,2; y = 12

Xem đáp án

Đáp án C

Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:

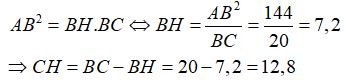
Vậy x = 7,2; y = 12,8

Câu 4:

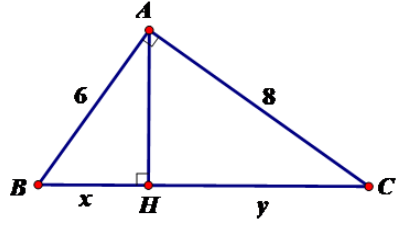
Tính x, y trong hình vẽ sau:

A. x = 3,6; y = 6,4

B. y = 3,6; x = 6,4

C. x = 4; y = 6

D. x = 2; y = 7,2

Xem đáp án

Đáp án A

Theo định lý Pytago ta có:

$B C^{2} = A B^{2} + A C^{2} \Leftrightarrow B C^{2}$ = 100 ⇔ BC = 10

Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:

Vậy x = 3,6; y = 6,4

Câu 5:

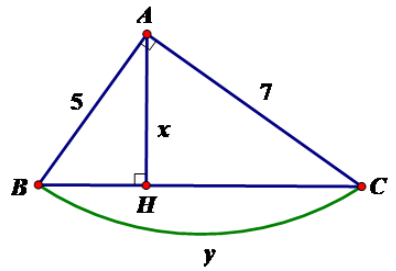
Tính x, y trong hình vẽ sau:

A. $x = \frac{35 \sqrt{74}}{74}; y = \sqrt{74}$

B. $y = \frac{35 \sqrt{74}}{74}; x = \sqrt{74}$

C. x = 4; y = 6

D. x = 2,8; y = 7,2

Xem đáp án

Đáp án A

Theo định lý Pytago ta có:

$B C^{2} = A B^{2} + A C^{2} \Leftrightarrow B C^{2} = 74$

⇔ BC = $\sqrt{74}$

Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:

Câu 6:

Cho tam giác ABC vuông tại A, đường cao AH. Biết BH = 9cm; CH = 16cm.

Tìm khẳng định sai trong các khẳng định sau:

A. AH = 15 cm

B. AB = 15 cm

C. AC = 20 cm

D. AH = 12 cm

Xem đáp án

Đáp án D

Ta có : BC = BH + HC = 9 + 16 = 25 (cm)

Áp dụng hệ thức về cạnh và đường cao trong tam giác –vuông ta có:

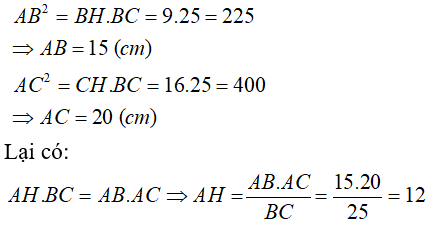
Câu 7:

Cho tam giác ABC vuông tại A, đường cao AH. Biết AH = 6cm; BH = 4,5 cm.

Tìm khẳng định đúng trong các khẳng định sau ?

A. AB = 10

B. AC = 7,5

C. BC= 12, 5

D. HC = 9

Xem đáp án

Đáp án C

Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông ta có:

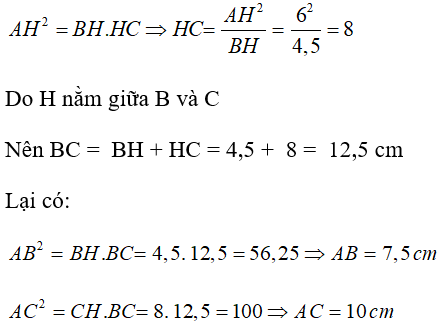
Câu 8:

Cho tam giác ABC vuông tại A, đường cao AH. Tính diện tích tam giác ABC biết AH = 12 cm; BH = 9cm.

A. 100 $c m^{2}$

B. 150 $c m^{2}$

C. 125 $c m^{2}$

D. 200 $c m^{2}$

Xem đáp án

Đáp án B

Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông ta có:

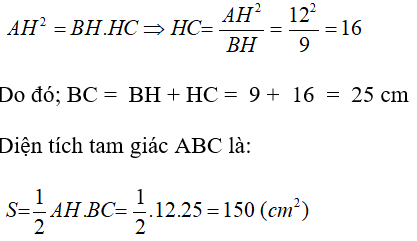
Câu 9:

Cho tam giác ABC vuông tại A. Biết $\frac{A B}{A C} = \frac{5}{6}$ , đường cao AH = 30 cm. Tính AB?

A. $5 \sqrt{61} (c m)$

B. $4 \sqrt{31} (c m)$

C. $5 \sqrt{31} (c m)$

D. $7 \sqrt{39} (c m)$

Xem đáp án

Đáp án A

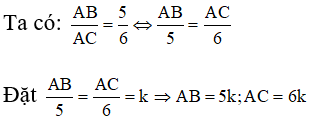
Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông ta có:

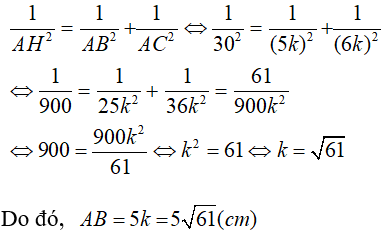
Câu 10:

Cho một tam giác vuông. Biết tỉ số hai cạnh góc vuông là 3 : 4 và cạnh huyền là 125cm. Tính độ dài các cạnh của tam giác vuông đã cho?

A. 50 và 75

B. 25 và 75

C. 75 và 100

D. 60 và 80

Xem đáp án

Đáp án C

Gọi tam giác vuông đã cho là tam giác ABC vuông tại A; AB < AC và đường cao AH.

Theo giả thiết tỉ số hai cạnh góc vuông là 3 : 4 nên

Do đó, AB = 3.25 = 75 cm và AC = 4.25 = 100cm

Bắt đầu thi ngay

CHỌN BỘ SÁCH BẠN MUỐN XEM

Bài 1 (có đáp án): Một số hệ thức về cạnh và đường cao trong tam giác vuông

Bài 1 (có đáp án): Một số hệ thức về cạnh và đường cao trong tam giác vuông

Danh sách câu hỏi

Có thể bạn quan tâm

Các bài thi hot trong chương