Bài tập theo tuần Toán 9 - Tuần 13
-
499 lượt thi
-
10 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Cho hàm số y = ax - 2. Xác định hệ số a trong các trường hợp sau :
a) Đồ thị hàm số song song với đường thẳng
b) Khi x = -3 thì hàm số có giá trị y = 7
 Xem đáp án
Xem đáp án
a) Để đồ thị hàm số y = ax - 2 song song với đường thẳng thì
b) Khi
Câu 2:
Cho đường thẳng
a) Tìm k để đồ thị hàm số (1) đi qua gốc tọa độ
b) Tìm giá trị của k để đồ thị (1) cắt trục tung tại điểm có tung độ bằng
c) Tìm giá trị của k để đồ thị (1) song song với đường thẳng
 Xem đáp án
Xem đáp án
a) Để đi qua gốc tọa độ
b) Đồ thị hàm số (1) cắt trục tung tại điểm có tung độ là
c) Đề đồ thị (1) song song với đường thẳng :
Câu 3:
Cho hai đường thẳng và . Viết phương trình đường thẳng biết và cắt tại điểm có hoành độ bằng -1.
 Xem đáp án
Xem đáp án
Gọi . Vì
Vì cắt tại điểm có hoành độ bằng
Thay x = -1, y = -4 vào ta có:
Vậy
Câu 4:
Cho hàm số y = ax + 4 đi qua A(3; -2). Tìm a. Vẽ đồ thị với a vừa tìm được
 Xem đáp án
Xem đáp án
Vì đồ thị hàm số y = ax + 4 qua A(3; -2)
Ta có hàm số y = -2x + 4 Học sinh tự vẽ đồ thị
Câu 5:
 Xem đáp án
Xem đáp án
Vì y = 3x + b cắt trục tung tại điểm có tung độ bằng y = -3
Câu 6:
Cho 2 hàm số
a) Vẽ đồ thị hai hàm số. Tìm tọa độ giao điểm
b) Một đường thẳng song song với trục Ox, cắt trục tung Oy tại điểm có tung độ bằng 1, cắt đường thẳng tại 2 điểm M, N. Tìm tọa độ hai điểm M, .N
 Xem đáp án
Xem đáp án
a) Học sinh tự vẽ hai đồ thị hàm số
Ta có phương trình hoành độ giao điểm là :
Vậy tọa độ giao điểm (0; 2)
b) Ta có
Cắt trục tung tại tung độ bằng 1
Vậy
Câu 7:
Từ điểm A ở ngoài đường tròn (O; R), vẽ tiếp tuyến AB (B là tiếp điểm), C là điểm trên đường tròn (O) sao cho AC = AB
a) Chứng minh AC là tiếp tuyến của (O)
b) D là điểm trên AC. Đường thẳng qua C vuông góc với OD tại M. Cắt đường tròn (O) tại Chứng minh rằng DElà tiếp tuyến của (O)
 Xem đáp án
Xem đáp án
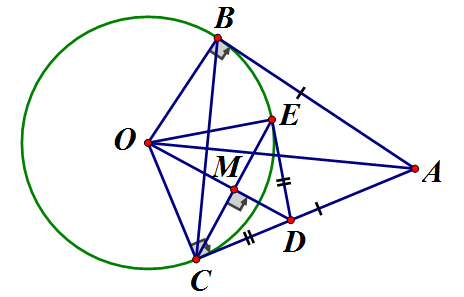
a) Xét và có:
(hai góc tương ứng) mà và là tiếp tuyến của (O)
b) Vì tại M M là trung điểm của CE là đường trung trực của CE
Xét và có chung
mà nên ED là tiếp tuyến của (O)
Câu 8:
Cho cân tại A, các đường cao AD, BE cắt nhau tại H. Vẽ đường tròn (O) có đường kính AH. Chứng minh rằng:
a) Điểm E nằm trên đường tròn (O)
b) DE là tiếp tuyến của (O)
 Xem đáp án
Xem đáp án
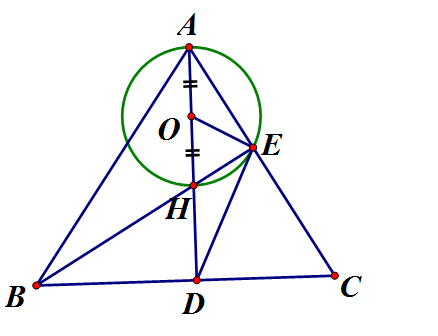
a) Ta có: vuông tại E , áp dụng định lý đường trung tuyến ứng với cạnh huyền
b) Ta có: vuông tại C nên DE = DB (tính chất đường trung tuyến ứng với cạnh huyền) vuông tại D nên
Mà (cùng phụ
Do cân tại O
Từ
mà là tiếp tuyến của (O)
Câu 9:
Cho nửa đường tròn (O; R) đường kính AB. M là điểm di động trên nửa đường tròn. Qua M vẽ tiếp tuyến với nửa đường tròn. Gọi D, C lần lượt là hình chiếu của A, B trên tiếp tuyến ấy.
a) Chứng minh rằng AD + BC không đổi
b) Xác định vị trí điểm M để diện tích tứ giác ABCD lớn nhất
 Xem đáp án
Xem đáp án
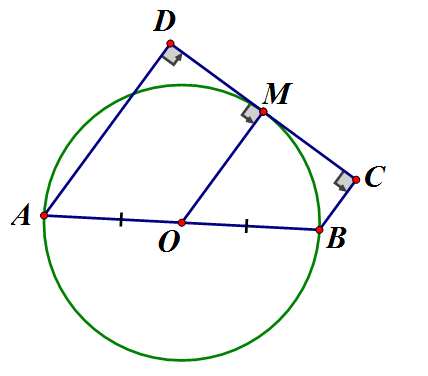
Hình thang ABCD (AB // CD) có là trung điểm của là trung điểm của CD
Ta có OM là đường trung bình của hình thang không đổi
b) Vẽ tại E
Tứ giác ADCE có nên là hình chữ nhật
Do đó
Nên không đổi
Dấu "=" xảy ra là giao điểm của đường thẳng vuông góc với AB vẽ từ O và đường tròn (O)
Vậy khi M là giao điểm của đường thẳng vuông góc với OB vẽ từ (O) và đường tròn (O) thì diện tích ABCD lớn nhất
Câu 10:
Cho đường tròn (O) bán kính OA, dây CD là đường trung trực của OA
a) Tứ giác OCAD là hình gì ? Vì sao ?
b) Kẻ tiếp tuyến với đường tròn tại C. Tiếp tuyến này cắt đường thẳng OA tại I. Tính độ dài CI biết OA = R.
 Xem đáp án
Xem đáp án
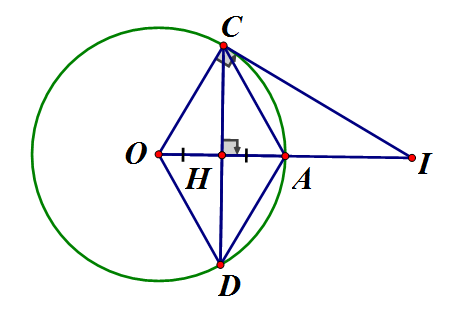
a) Ta có: tại là trung điểm CD
Tứ giác OCAD có hai đường chéo CD và OA vuông góc nhau tại trung điểm mỗi đường nên OCAD là hình thoi
b) Ta có: H là trung điểm
Áp dụng định lý Pytago vào vuông tại H, ta có:
vuông tại C, CH đường cao, áp dụng hệ thức lượng ta có:
