7 câu hỏi trắc nghiệm thuộc Bài tập theo tuần Toán 9 - Tuần 14

Câu 1:

Trên mặt phẳng tọa độ Oxy, cho hai điểm $A (- 1; - 1); B (2; 5) .$

a) Biết đồ thị của nó là đường thẳng đi qua A, B. Tìm hàm số đó

b) Tìm hệ số góc của đường thẳng đi qua A, B

a) Gọi $(d) y = a x + b$ là hàm số cần tìm

Vì $A (- 1; 1); B (2; 5) \in (d) \Rightarrow \{\begin{cases} - a + b = 1 \\ 2 a + b = 5 \end{cases} \Leftrightarrow \{\begin{cases} a = \frac{4}{3} \\ b = \frac{7}{3} \end{cases}$

$\Rightarrow (d) : y = \frac{4}{3} x + \frac{7}{3}$

b) Hệ số góc $a = \frac{4}{3}$

Câu 2:

Cho hàm số $y = (m + 1) x - 2 m + 1 (d)$

a) Xác định m để đường thẳng (d) đi qua gốc tọa độ

b) Tìm m để đường thẳng (d) đi qua A(3; 4).Vẽ đồ thị vừa tìm được

c) Tìm tọa độ giao điểm của đường thẳng vừa vẽ với đt $(d') y = - 2 x + 4$

d) Tìm số đo góc $α$ tạo bởi đường thẳng (d') với trục Ox.

Xem đáp án

$y = (m + 1) x - 2 m + 1 (d)$

a) Để (d) đi qua gốc tọa độ $\Rightarrow \{\begin{cases} m + 1 \neq 0 \\ - 2 m + 1 = 0 \end{cases} \Leftrightarrow m = \frac{1}{2}$

b) Để (d) đi qua $A (3; 4) \Rightarrow 4 = (m + 1) .3 - 2 m + 1 \Leftrightarrow m = 0$

Học sinh tự vẽ đồ thị.

c) Ta có: $(d) : y = x + 1 (d') : y = - 2 x + 4$

Ta có phương trình hoành độ giao điểm của (d) và (d') là:

$x + 1 = - 2 x + 4 \Leftrightarrow 3 x = 3 \Leftrightarrow x = 1 \Rightarrow y = 2$

Vậy A(1; 2) là tọa độ của (d) và (d')

$d) (d') : y = - 2 x + 4$

Ta có: $\tan β = \frac{4}{2} = 2 \Rightarrow α \approx 63^{0}$

$\Rightarrow$ góc $α$ tạo bởi (d') với Ox là: $α = 180^{0} - 63^{0} = 117^{0}$

Câu 3:

Cho hàm số bậc nhất y = -2x + 3

a) Hàm số đã cho đồng biến hay nghịch biến ? Vì sao ?

b) Vẽ đồ thị (d) của hàm số trên.

c) Gọi M là điểm có tọa độ $(a; b) \in$ đồ thị (d) nói trên. Xác định a, b biết rằng $\sqrt{a} . (\sqrt{b} + 1) = 2$

Xem đáp án

a) $a = - 2 < 0 \Rightarrow y = - 2 x + 3$ nghịch biến trên R

b) Học sinh tự vẽ

c) Ta có: $y = - 2 x + 3 M (a; b) \in (d) \Rightarrow - 2 a + 3 = b \Rightarrow 3 = 2 a + b$

Ta có:

$\begin{array}{l} \sqrt{a} (\sqrt{b} + 1) = 2 \\ \Leftrightarrow 2 \sqrt{a} (\sqrt{b} + 1) = 4 \\ \Leftrightarrow 2 \sqrt{a b} + 2 \sqrt{a} = 3 + 1 \\ \Leftrightarrow 2 \sqrt{a b} + 2 \sqrt{a} = 2 a + b + 1 \\ \Leftrightarrow 2 a + b + 1 - 2 \sqrt{a b} - 2 \sqrt{a} = 0 \\ \Leftrightarrow (a - 2 \sqrt{a b} + b) + (a - 2 \sqrt{a} + 1) = 0 \\ \Leftrightarrow {(\sqrt{a} - \sqrt{b})}^{2} + {(\sqrt{a} - 1)}^{2} = 0 \\ \Rightarrow \{\begin{cases} \sqrt{a} - \sqrt{b} = 0 \\ \sqrt{a} - 1 = 0 \end{cases} \Rightarrow a = b = 1 \end{array}$

Câu 4:

M là điểm tùy ý thuộc đường thẳng cố định d nằm ngoài đường tròn (O; R). Từ M kẻ hai tiếp tuyến MP, MQ với đường tròn (O) (P, Q là các tiếp điểm). Hạ OH vuông góc với đường thẳng d. Dây cung PQ cắt OH ở I, cắt OM ở K. Chứng minh rằng:

a) $O I . O H = O K . O M = R^{2}$

b) Khi M thay đổi trên đường thẳng d thì vị trí của điểm I luôn luôn không đổi

Xem đáp án

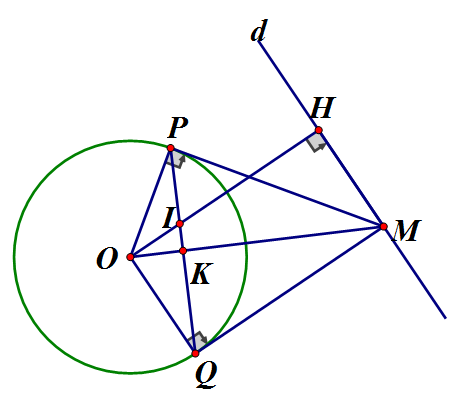
M là điểm tùy ý thuộc đường thẳng cố định d nằm ngoài đường tròn (O; R). (ảnh 1)

a) Theo tính chất hai tiếp tuyến cắt nhau, ta có:

MP = MQ và MO là tia phân giác của $\hat{P M Q}$ nên $O M ⊥ P Q$ tại K

Ta có: $Δ O K I ~ Δ O H M$ (vì có $\hat{K O I}$ chung)

$\Rightarrow \hat{O K I} = \hat{O H M} = 90^{0} \Rightarrow \frac{O K}{O H} = \frac{O I}{O M} \Rightarrow O H . O I = O K . O M$

Vì MP, MQ là các tiếp tuyến của (O) nên $O P ⊥ M P, O Q ⊥ M Q$

$Δ O P M$ có PK là đường cao nên $O K . O M = O P^{2} = R^{2}$

Vậy $O I . O H = O K . O M = R^{2}$

b) Vì đường thẳng d cố định, đường tròn (O) cố định nên OH cố định và có độ dài không đổi , mà $O I . O H = R^{2}$ không đổi nên $O I = \frac{R^{2}}{O H}$ không đổi

I ở trên tia OH cố định và có OI không đổi nên I cố định.

Câu 5:

Cho $Δ A B C$ nhọn. Đường tròn tâm O, đường kính BC cắt AB ở M và cắt AC ở N. Gọi H là giao điểm của BN và CM. AH cắt BC tại K

a) Chứng minh $A K ⊥ B C$

b) Gọi E là trung điểm của AH. Chứng minh EM là tiếp tuyến của đường tròn (O)

c) Cho biết $\sin \overset{}{B A C} = \frac{\sqrt{2}}{2}$ . Hãy so sánh AH và BC.

Xem đáp án

Cho tam giác ABC nhọn. Đường tròn tâm O, đường kính BC cắt AB ở M và cắt AC ở N (ảnh 1)

a) $Δ B M C$ có $O M = O B = O C = \frac{B C}{2} = R \Rightarrow Δ B M C$ vuông tại M (định lý đảo đường trung tuyến ứng với cạnh huyền)

$\Rightarrow B M ⊥ M C (1), C m t t \Rightarrow B N ⊥ N C (2)$

Từ (1) và (2) suy ra BN, CM là hai đường cao của tam giác $A B C \Rightarrow H$ là trực tâm $Δ A B C$ $\Rightarrow A K ⊥ B C .$

b) $Δ A M H$ vuông tại M, ME là đường trung tuyến $\Rightarrow A E = E M \Rightarrow Δ A E M$ cân $\Rightarrow \hat{A E M} = \hat{E M A} (3)$ mà $\hat{E M A} = \hat{O C M}$ (cùng phụ với góc B) (4)

Và $\hat{O C M} = \hat{O M C}$ (tính chất tam giác cân ) (5)

Từ $(3), (4), (5) \Rightarrow \hat{E M A} = \hat{O M C}$ mà $\hat{E M A} + \hat{E M H} = 90^{0}$

$\Rightarrow \hat{O M C} + \hat{E M H} = 90^{0} \Rightarrow \hat{E M O} = 90^{0}, M \in (O)$ $\Rightarrow$ EM là tiếp tuyến của (O)

c) Vì $\sin \hat{B A C} = \frac{\sqrt{2}}{2} \Rightarrow \hat{B A C} = 45^{0} \Rightarrow Δ A M C$ vuông cân tại M $\Rightarrow A M = M C$

Xét $Δ A M H$ và $Δ C M B$ có: $\hat{M A H} = \hat{M C B}$ (cùng phụ góc B); AM = CM

$\hat{A M H} = \hat{B M C} = 90^{0} \Rightarrow Δ A M H = Δ C M B \Rightarrow A H = B C$

Câu 6:

Cho nửa đường tròn (O) đường kính AB. Kẻ hai tiếp tuyến Ax, By (Ax, By và nửa đường tròn thuộc cùng nửa mặt phẳng bờ AB). Gọi Clà một điểm trên tia Ax, kẻ tiếp tuyến CM với nửa đường tròn (Mlà tiếp điểm), CM cắt By ở D

a) Tính số đo $\hat{C O D}$

b) Gọi I là giao điểm của $O C, A M, K$ là giao điểm của OD và MB. Tứ giác OIMK là hình gì ? Vì sao ?

c) Chứng minh tích AC.BD không đổi khi C di chuyển trên Ax

d) Chứng minh AB là tiếp tuyến của đường tròn đường kính CD

Xem đáp án

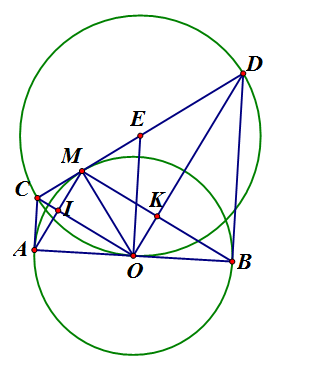
Cho nửa đường tròn (O) đường kính AB. Kẻ hai tiếp tuyến Ax, By (Ax, By (ảnh 1)

a) Vì CM, CA là hai tiếp tuyến cắt nhau nên $\hat{M O C} = \hat{A O C} = \frac{1}{2} \hat{A O M}$

Chứng minh tương tự $\Rightarrow \hat{M O D} = \hat{D O B} = \frac{1}{2} \hat{M O B}$

$\Rightarrow \hat{C O D} = \hat{C O M} + \hat{M O D} = \frac{1}{2} (\hat{A O M} + \hat{M O B})$ $= \frac{1}{2} \hat{A O B} = \frac{1}{2} {.180}^{0} = 90^{0}$

Vậy $\hat{C O D} = 90^{0}$

b) Cũng theo tính chất hai tiếp tuyến cắt nhau $\Rightarrow O C$ là trung trực của AM $\Rightarrow \hat{I} = 90^{0}$

Chứng minh tương tự $\Rightarrow \hat{K} = 90^{0}$

Tứ giác MIOK có $\hat{C O D} = \hat{I} = \hat{K} = 90^{0} \Rightarrow O I M K$ là hình chữ nhật

c) Theo tính chất hai tiếp tuyến cắt nhau $\Rightarrow \{\begin{cases} A C = M C \\ B D = M D \end{cases} \Rightarrow A C . M D = M C . M D$

Áp dụng hệ thức lượng vào $Δ C O D$ vuông tại O, OM đường cao $\Rightarrow M C . M D = O M^{2} = R^{2}$

Vậy $A C . B D = R^{2}$ không đổi .

d) Gọi E là trung điểm CD. Ta có CA // DB (cùng vuông góc với $A B) \Rightarrow C A B D$ là hình thang có E là trung điểm CD, O là trung điểm $A B \Rightarrow E O$ là đường trung bình hình thang $C A B D \Rightarrow E O ⊥ A B$ và OE = OC = OD (tính chất đường trung tuyến ứng với cạnh huyền) $\Rightarrow O \in (E; E D)$ và $E O ⊥ A B$ nên AB là tiếp tuyến của (E)

Câu 7:

Cho tam giác nhọn ABC có AD, BE, CF là ba đường cao cắt nhau tại H. M, N lần lượt là hình chiếu của B, C trên đường thẳng EF. Chứng minh rằng:

a) $Δ A E F ~ Δ A B C$

b) H là tâm đường tròn nội tiếp $Δ D E F$

c) A, B, C là tâm đường tròn bàng tiếp của $Δ D E F$

d) $D E + D F = M N$

Xem đáp án

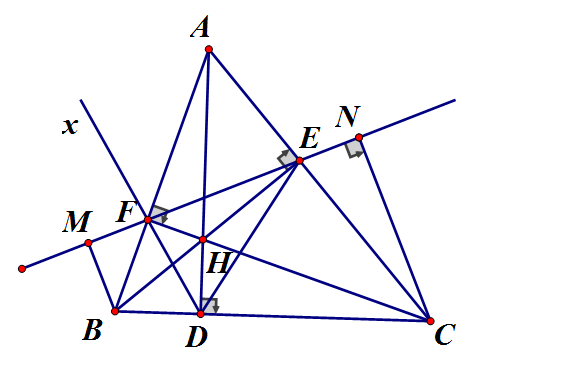
Cho tam giác nhọn ABC có AD, BE, CF là ba đường cao cắt nhau tại H. M, N (ảnh 1)

a) Xét $Δ A B E$ và $Δ A C F$ có $\hat{B A E}$ chung; $\hat{A E B} = \hat{A F C} = 90^{0}$

$\Rightarrow Δ A B E ~ Δ A C F (g . g) \Rightarrow \frac{A B}{A C} = \frac{A E}{A F}$

Xét $Δ A E F$ và $Δ A B C$ có: $\hat{E A F}$ chung; $\frac{A E}{A B} = \frac{A F}{A C} (c m t) \Rightarrow Δ A E F ~ Δ A B C$

b) $Δ A E F ~ Δ A B C \Rightarrow \hat{A E F} = \hat{A B C}$

cmtt $\Rightarrow \hat{D E C} = \hat{A B C} \Rightarrow \hat{A E F} = \hat{D E C}$

Ta có $\hat{D E C} + \hat{H E D} = \hat{A E F} + \hat{H E F} (= 90^{0})$ nên $\hat{H E D} = \hat{H E F} \Rightarrow E H$ là đường phân giác của $Δ D E F$ . Chứng mnh tương tự ta cũng có DH là đường phân giác $Δ D E F \Rightarrow H$ là tâm đường tròn nội tiếp $Δ D E F$

c) Gọi Fx là tia đối của tia FD

Ta có: $\hat{x F A} + \hat{D F C} = \hat{A F E} + \hat{E F C} (= 90^{0})$ mà $\hat{D F C} = \hat{E F C}$ , do đó $\hat{x F A} = \hat{A F E}$

A là giao điểm của đường phân giác $\hat{D}$ và đường phân giác ngoài đỉnh F nên A là tâm đường tròn bàng tiếp trong góc D của $Δ D E F .$ Chứng minh tương tự ta cũng có B, C là tâm đường tròn bàng tiếp $Δ D E F .$

d) Theo bài $P_{D E F} = 2 E M, P_{D E F} = 2 N F$

$\begin{array}{l} \Rightarrow D E + D F + E F = E M + N F \\ \Rightarrow D E + D F + E F = M N - E N + N F \\ \Leftrightarrow D E + D F + E F = M N + E F \\ \Leftrightarrow D E + D F = M N \end{array}$

CHỌN BỘ SÁCH BẠN MUỐN XEM

Bài tập theo tuần Toán 9 - Tuần 14

Bài tập theo tuần Toán 9 - Tuần 14

Danh sách câu hỏi

Có thể bạn quan tâm

Các bài thi hot trong chương