Bài tập Toán 9 Chủ đề 6: Hàm số bậc hai và các bài toán tương giao với đồ thị hàm số bậc nhất có đáp án
Dạng 2. Sự tương giao giữa đường thẳng và đồ thị hàm số bậc hai.
-
1064 lượt thi
-
33 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Trong mặt phẳng với hệ tọa độ , cho parabol và đường thẳng
Vẽ đồ thị của (P)
 Xem đáp án
Xem đáp án
HS tự vẽ.
Câu 2:
Gọi và lần lượt là các giao điểm của (P) với (d). Tính giá trị biểu thức .
 Xem đáp án
Xem đáp án
Phương trình hoành độ giao điểm của (P) và (d):
. Vậy
Câu 3:
Cho Parabol và đường thẳng (m là tham số)
Chứng minh rằng với mọi m đường thẳng d luôn cắt (P) tại hai điểm phân biệt Xem đáp án
Xem đáp án
Phương trình hoành độ giao điểm
Ta có
Vậy Parabol luông cắt đường thẳng tại hai điểm phân biệt.
Câu 4:
 Xem đáp án
Xem đáp án
Vì là nghiệm của phương trình nên theo hệ thức Vi-et ta có: .
Mặt khác .
Ta có
Vậy .
Câu 5:
Cho parabol và đường thẳng (với a là tham số )
Tìm tọa độ giao điểm của (P) và (d) khi .
 Xem đáp án
Xem đáp án
Phương trình hoành độ (d) và (P) là
Khi thì phương trình trở thành
Có nên phương trình có 2 nghiệm là ; .
Câu 6:
Tìm tất cả các giá trị của a để đường thẳng (d) cắt (P) taị hai điểm phân biệt có hoành độ thỏa mãn .
 Xem đáp án
Xem đáp án
Phương trình hoành độ (d) và (P) là (*)
để đường thẳng (d) cắt (P) tại hai điểm phân biệt thì phương trình (*) phải có 2 nghiệm phân biệt
Với theo Viét ta có
Vì
Với :
Với :
Vậy .
Câu 7:
Cho hai hàm số và , với m là tham số.
Khi m=3, tìm tọa độ các giao điểm của hai đồ thị hàm số trên.
 Xem đáp án
Xem đáp án
Phương trình hoành độ giao điểm của và là (1)
Thay vào phương trình (1) ta có:
Ta có:
Vậy phương trình có hai nghiệm
Với
Với
Vậy với thì hai đồ thị hàm số giao nhau tại 2 điểm và .
Câu 8:
 Xem đáp án
Xem đáp án
Ta có số giao điểm của hai đồ thị hàm số đã cho là số nghiệm của phương trình (1)
Phương trình (1) có:
Do đó (1) luôn có hai nghiệm phân biệt
Vậy đồ thị của hai hàm số đã cho luôn cắt nhau tại hai điểm phân biệt và với mọi m
Theo hệ thức Vi-et ta có:
Ta lại có:
Theo đề, ta có:
(trường hợp vô nghiệm vì )
Vậy với thì .
Câu 10:
Cho hàm số có đồ thị (P) .Cho đường thẳng . Tìm m,n để đường thẳng song song với đường thẳng và có duy nhất một điểm chung với đồ thị .
 Xem đáp án
Xem đáp án
song song với suy ra
Phương trình hoành độ giao điểm của và (P):
(*)
Để và (P) có một điểm chung duy nhất thì phương trình (*) có nghiệm duy nhất thì (thỏa mãn)
Vậy .
Câu 11:
Cho đường thẳng (d) có phương trình và parabol (P) có phương trình . Vẽ đường thẳng (d) và parabol (P) trên cùng hệ trục tọa độ .
 Xem đáp án
Xem đáp án
HS tự vẽ đồ thị hàm số (d) và (P)
Câu 12:
Cho đường thẳng (d) có phương trình y=x+2 và parabol (P) có phương trình . Đường thẳng (d) cắt (P) tại hai điểm A và B (với A có hoành độ âm, B có hoành độ dương). Bằng tính toán hãy tìm tọa độ các điểm A và B.
 Xem đáp án
Xem đáp án
Phương trình hoành độ giao điểm của (d) và (P):
hoặc
Với (vì B có hoành độ dương)
Với (vì A có hoành độ âm)
Vậy ;
Câu 13:
Cho hai hàm số và đồ thị hàm số (P) và có đồ thị (d) .Vẽ đồ thị (P)
 Xem đáp án
Xem đáp án
Vẽ đồ thị: HS tự vẽ
Câu 14:
Cho hai hàm số và đồ thị hàm số (P) và có đồ thị (d). Gọi A,B là các giao điểm của hai đồ thị (P) và (d). Biết rằng đơn vị đo trên các trục tọa độ là xentimét, tìm tất cả các điểm M trên tia Ox sao cho diện tích tam giác MAB bằng 30 cm2.
 Xem đáp án
Xem đáp án
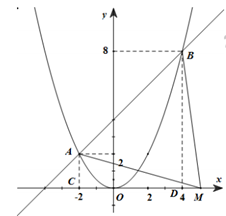
Phương trình có 2 nghiệm phân biệt:
Với ta có
Với ta có
Gọi thuộc tia Gọi
Xét hai trường hợp:
Trường hợp 1: M thuộc đoạn OD: Ta có
Có là hình thang,
⇒
Suy ra cm2 (loại)
Trường hợp 2: M thuộc tia Dx
Ta có :
Có
Suy ra
m = 6 (thỏa mãn). Vậy là điểm cần tìm.
Câu 15:
Trong mặt phẳng tọa độ Oxy cho đường thẳng và parabol . Chứng minh (d) luôn cắt (P) tại hai điểm phân biệt với mọi m.
 Xem đáp án
Xem đáp án
Xét phương trình hoành độ giao điểm của (d) và (P)
Suy ra phương trình (*) luôn có hai nghiệm phân biệt với mọi m hay (d) luôn cắt (P) tại hai điểm phân biệt với mọi m.
Câu 16:
Trong mặt phẳng tọa độ Oxy cho đường thẳng và parabol . Gọi là hoành độ các giao điểm của (d) và (P). Tìm m để
 Xem đáp án
Xem đáp án
Ta có: (**)
Áp dụng hệ thức Vi-et cho (*):
Vậy .
Câu 18:
Trong mặt phẳng toạ độ Oxy, cho parabol .Xác định toạ độ các giao điểm A,B của đường thẳng (d') và (P). Tìm toạ điểm M trên (P) sao cho tam giác MAB cân tại M.
 Xem đáp án
Xem đáp án
Viết phương trình đường trung trực của , tìm giao điểm của và ta tìm được giao điểm M.
Hoành độ các giao điểm của đường thẳng và (P) là nghiệm của phương trình: hoặc x=2
+ Với , thay vào (P) ta có: , ta có:
+ Với , thay vào (P) ta có: , ta có:
Suy ra trung điểm của AB là:
Đường thẳng vuông góc với (d) có dạng:
Vì đi qua I nên:
Vậy
Phương trình hoành độ của (d') và (P) là:
+ Với
+ Với
Vậy có hai điểm M cần tìm là: và .
Câu 19:
Trong mặt phẳng tọa độ Oxy cho đường thẳng và parabol .Tìm m để (d) đi qua điểm
 Xem đáp án
Xem đáp án
Thay vào phương trình đường thẳng (d) ta được:
Câu 20:
Trong mặt phẳng tọa độ Oxy cho đường thẳng và parabol . Tìm m để đường thẳng (d) cắt parabol (P) tại hai điểm phân biệt có hoành độ lần lượt là thỏa mãn: .
 Xem đáp án
Xem đáp án
Phương trình hoành độ giao điểm của (d) và (P) là:
Để (d) cắt parabol (P) tại hai điểm phân biệt thì phương trình (*) phải có 2 nghiệm phân biệt
Khi đó theo định lý Vi-ét ta có:
Theo đề bài:
( Điều kiện: )
(loại) hoặc (thỏa mãn).
Vậy là giá trị cần tìm.
Câu 21:
Trong mặt phẳng tọa độ Oxy cho Parabol và đường thẳng (với m là tham số). Tìm m để đường thẳng (d) đi qua điểm
 Xem đáp án
Xem đáp án
Câu 22:
Trong mặt phẳng tọa độ Oxy cho Parabol và đường thẳng (với m là tham số). Xác định các giá trị của m để (d) cắt (P) tại hai điểm phân biệt sao cho tổng 2 tung độ của hai giao điểm đó bằng -10
 Xem đáp án
Xem đáp án
Phương trình hoành độ giao điểm của đường thẳng (d) và Parabol (P) là:
Ta có , với mọi m nên phương trình (*) có hai nghiệm phân biệt.
Do đó, đường thẳng (d) và Parabol (P) cắt nhau tại hai điểm và
Theo định lý Vi-ét ta có:
Theo bài ra ta có:
Vậy là giá trị cần tìm.
Câu 23:
Cho parabol và đường thẳng (d) có phương trình: .Tìm tọa độ giao điểm của (P) và (d) với m=3.
 Xem đáp án
Xem đáp án
Thay m=3 ta được
Phương trình hoành độ giao điểm (P) và (d) khi m=3 là
Giải phương trình ta được . Với ;
Tọa độ giao điểm của (P) và (d) là
Câu 24:
Chứng minh (P) và (d) luôn cắt nhau tại 2 điểm phân biệt A và B với mọi m.
 Xem đáp án
Xem đáp án
Xét phương trình hoành độ giao điểm của (P) và (d) là:
(1)
Nên phương trình (1) có hai nghiệm phân biệt suy ra (P) và (d) luôn cắt nhau tại 2 điểm phân biệt với mọi m.
Câu 25:
Gọi là hoành độ giao điểm của A và B. Tìm m để .
 Xem đáp án
Xem đáp án
Ta có: là nghiệm phương trình (1) vì . Theo Vi-et ta có:
Vậy hoặc là giá trị cần tìm.
Câu 26:
Cho parabol và đường thẳng (m là tham số).
Với , tìm tọa độ giao điểm của parabol (P) và đường thẳng (d)
 Xem đáp án
Xem đáp án
Với có phương trình
Hoành độ giao điểm của (P) và (d) là nghiệm phương trình:
Vậy với thì (P) và (d) cắt nhau tại hai điểm
Câu 27:
Chứng minh rằng: với mọi m parabol (P) và đường thẳng (d) cắt nhau tại hai điểm phân biệt. Tìm m sao cho hai giao điểm đó có hoành độ dương.
 Xem đáp án
Xem đáp án
Hoành độ giao điểm của (P) và (d) là nghiệm phương trình:
Do đó (1) có hai nghiệm phân biệt với mọi m suy ra (P) và (d) cắt nhau tại hai điểm phân biệt là hai nghiệm của phương trình (1), áp dụng định lý Viet ta có:
Hai giao điểm đó có hoành độ dương khi và chỉ khi
Vậy với thì (P) và (d) cắt nhau tại hai điểm phân biệt với hoành độ dương.
Câu 28:
Tìm điểm cố định mà đường thẳng (d) luôn đi qua với mọi m
 Xem đáp án
Xem đáp án
Gọi điểm cố định mà đường thẳng đi qua với mọi m là ta có:
Vậy với mọi m thì đường thẳng (d) luôn đi qua
Câu 29:
Trong mặt phẳng tọa độ cho đường thẳng tham số m và Parabol
Tìm m để đường thẳng (d) đi qua điểm A(1;0)
 Xem đáp án
Xem đáp án
Câu 30:
 Xem đáp án
Xem đáp án
Xét phương trình hoành độ giao điểm giữa (P) và (d):
Có
(d) cắt (P) tại hai điểm phân biệt có hoành độ lần lượt là khi
Áp dụng hệ thức Vi – Ét ta có:
Theo bài ra ta có
Vậy là giá trị cần tìm.
Câu 31:
Cho hàm số có đồ thị và đường thẳng
Tìm a để đồ thị (P) đi qua điểm B(2;-2).
Chứng minh rằng đường thẳng (d) luôn cắt đồ thị (P) tại hai điểm phân biệt C và D với mọi giá trị của m
 Xem đáp án
Xem đáp án
(P) đi qua điểm nên ta có:
Vậy :
Câu 32:
Cho hàm số có đồ thị và đường thẳng
Chứng minh rằng đường thẳng (d) luôn cắt đồ thị (P) tại hai điểm phân biệt C và D với mọi giá trị của m
 Xem đáp án
Xem đáp án
Phương trình hoành độ giao điểm của (d) và (P) là:
Do đó, đường thẳng (d) luôn cắt đồ thị (P) tại hai điểm phân biệt C và D với mọi giá trị của m.
Câu 33:
Gọi và lần lượt là hoành độ của hai điểm C và D. Tìm các giá trị của m sao cho
 Xem đáp án
Xem đáp án
Áp dụng định lí Vi-ét ta có:
Theo giả thiết
. Vậy với thỏa mãn yêu cầu bài toán.
