Đề ôn thi vào 10 môn Toán có đáp án (Mới nhất) - Đề số 7
-
3922 lượt thi
-
5 câu hỏi
-
120 phút
Danh sách câu hỏi
Câu 1:
Cho biểu thức: \(P = \left( {\frac{1}{{x - \sqrt x }} + \frac{1}{{\sqrt x - 1}}} \right):\frac{{\sqrt x + 1}}{{{{\left( {\sqrt x - 1} \right)}^2}}}\).
1) Tìm điều kiện xác định và rút gọn biểu thức P?
2) Tìm tất cả các giá trị của x để \(P = \frac{1}{3}\)?
3) Tìm giá trị lớn nhất của biểu thức \(Q = A - 9\sqrt x \)?
 Xem đáp án
Xem đáp án
1) Điều kiện xác định: \(\left\{ \begin{array}{l}x - \sqrt x \ne 0\\\sqrt x - 1 \ne 0\\x \ge 0\\\sqrt x + 1 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ne 0\\x \ne 1\\x \ge 0\\\sqrt x \ne - 1\end{array} \right. \Leftrightarrow 0 < x \ne 1\)
Ta có: \(P = \left( {\frac{1}{{x - \sqrt x }} + \frac{1}{{\sqrt x - 1}}} \right).\frac{{{{\left( {\sqrt x - 1} \right)}^2}}}{{\sqrt x + 1}}\)
\( = \left[ {\frac{1}{{x - \sqrt x }} + \frac{{\sqrt x }}{{\sqrt x \left( {\sqrt x - 1} \right)}}} \right].\frac{{{{\left( {\sqrt x - 1} \right)}^2}}}{{\sqrt x + 1}}\)
\( = \frac{{1 + \sqrt x }}{{\sqrt x \left( {\sqrt x - 1} \right)}}.\frac{{{{\left( {\sqrt x - 1} \right)}^2}}}{{\sqrt x + 1}} = \frac{{{{\left( {\sqrt x - 1} \right)}^2}}}{{\sqrt x \left( {\sqrt x - 1} \right)}} = \frac{{\sqrt x - 1}}{{\sqrt x }}\)
Vậy \(P = \frac{{\sqrt x - 1}}{{\sqrt x }}\).
Cách 2: Đặt \(a = \sqrt x \) \(\left( {a \ge 0} \right)\)
Ta có: \(P = \left( {\frac{1}{{{a^2} - a}} + \frac{1}{{a - 1}}} \right):\frac{{a + 1}}{{{{\left( {a - 1} \right)}^2}}} = \left[ {\frac{1}{{a\left( {a - 1} \right)}} + \frac{1}{{a - 1}}} \right].\frac{{{{\left( {a - 1} \right)}^2}}}{{a + 1}}\)
\( = \left[ {\frac{{1 + a}}{{a\left( {a - 1} \right)}}} \right].\frac{{{{\left( {a - 1} \right)}^2}}}{{a + 1}} = \frac{{a - 1}}{a} = \frac{{\sqrt x - 1}}{{\sqrt x }}\).
Nhận xét: Bài toán tìm điều kiện và rút gọn áp dụng quy tắc tìm điều kiện và các phương pháp phân tích đa thức thành nhân tử.
2) Với \(P = \frac{1}{3} \Leftrightarrow \frac{{\sqrt x - 1}}{{\sqrt x }} = \frac{1}{3}\)
\( \Leftrightarrow 3\left( {\sqrt x - 1} \right) = \sqrt x \Leftrightarrow 2\sqrt x = 3 \Leftrightarrow x = \frac{9}{4}\) (thõa mãn).
Nhận xét: Bài toán tìm giá trị của biến để biểu thức nhận một giá trị cho trước.
3) Ta có \(Q = P - 9\sqrt x = \frac{{\sqrt x - 1}}{{\sqrt x }} - 9\sqrt x = 1 - \left( {\frac{1}{{\sqrt x }} + 9\sqrt x } \right)\)
Áp dụng bất đẳng thức Cô-si cho 2 số không âm \(\frac{1}{{\sqrt x }}\) và \(9\sqrt x \), tạ có:
\(\frac{1}{{\sqrt x }} + 9\sqrt x \ge 2\sqrt {\frac{1}{{\sqrt x }}.9\sqrt x } = 2\sqrt 9 = 6\).
\( \Rightarrow Q \le 1 - 6 = - 5\)
Dấu " = " xảy ra khi \(\frac{1}{{\sqrt x }} = 9\sqrt x \Leftrightarrow 1 = 9x \Leftrightarrow x = \frac{1}{9}\)
Vậy \(\max P = - 5\) khi \(x = \frac{1}{9}\).
Nhận xét: Bài toán tìm cực trị của biểu thức.
Câu 2:
1) Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình.
Cho tam giác ABC vuông tại A, có \(AB = 8cm,\,\,AC = 6cm\). M là một điểm trên AB. Qua M kẻ các đường thẳng song song với AC và BC lần lượt cắt BC và AC tại D và N. Hãy xác định điểm M để diện tích của hình bình hành MNCD bằng \(\frac{3}{8}\) diện tích của tam giác ABC?
2) Cho hàm số \(y = mx + 1\) (1)
a) Tìm \(m\) để đồ thị hàm số (1) đi qua điểm \(A\left( {1;4} \right)\) . Với giá trị \(m\) vừa tìm được, hàm số (1) đồng biến hay nghịch biến trên \(\mathbb{R}\)?
b) Tìm \(m\) để đồ thị hàm số (1) song song với đường thẳng \(\left( d \right):x + y + 3 = 0\).
 Xem đáp án
Xem đáp án
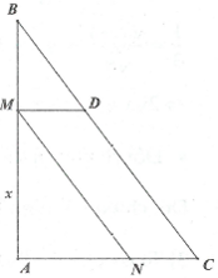
Gọi độ dài AM là x (cm), \(0 < x < 8\).
Theo định lý Ta-lét trong tam giác ABC với \(MN//BC\) ta có \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} \Leftrightarrow \frac{x}{8} = \frac{{AN}}{6} \Leftrightarrow AN = \frac{3}{4}x\left( {cm} \right)\)
\( \Rightarrow NC = AC - AN = 6 - \frac{3}{4}x\left( {cm} \right)\).
Diện tích hình bình hành \(MNCD\) là:
\({S_{MNCD}} = AM.NC = x\left( {6 - \frac{3}{4}x} \right)\left( {c{m^2}} \right)\)
Diện tích tam giác ABC là: \({S_{\Delta ABC}} = \frac{1}{2}AB.AC = \frac{1}{2}.6.8 = 24\left( {c{m^2}} \right)\)
Theo bài ra, diện tích của hình bình hành MNCD bằng \(\frac{3}{8}\) diện tích của tam giác ABC, nên ta có phương trình \(x\left( {6 - \frac{3}{4}x} \right) = \frac{3}{8}.24\)
\( \Leftrightarrow {x^2} - 8x + 12 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = 6\end{array} \right.\) (thỏa mãn điều kiện).
Vậy điểm M cách A là 2 cm hoặc 6 cm.
2)
a) Do đồ thị hàm số (1) đi qua điểm \(A\left( {1;4} \right)\) nên ta có phương trình \(4 = m.1 + 1 \Leftrightarrow m = 3\) .
Với \(m = 3\) hàm số (1) có dạng \(y = 3x + 1\)
Vì \(3 > 0\) nên hàm số (1) đồng biến trên \(\mathbb{R}\).
b) Phương trình đường thẳng \[\left( d \right)\] là: \(y = - x - 3\).
Để đồ thị hàm số (1) song song với đường thẳng \[\left( d \right)\] thì \(\left[ \begin{array}{l}m = - 1\\1 \ne - 3\end{array} \right. \Leftrightarrow m = - 1\)
Vậy \(m = - 1\) thì đồ thị của hàm số (1) song song với đường thẳng \[\left( d \right)\].
Câu 3:
1) Giải hệ phương trình \(\left\{ \begin{array}{l}x = 2 + z\\y = 2 + 3z\\z - 3x - 2y + 2 = 0\end{array} \right.\)
2) Giải phương trình: \(\sqrt {2{x^2} + 3x - 5} = 2x - 2\).
3) Cho phương trình \(\left( {m - 1} \right){x^2} - 2\left( {m + 2} \right)x + m + 1 = 0\). Tìm \(m\) để phương trình có nghiệm duy nhất?
 Xem đáp án
Xem đáp án
1) Hệ phương trình tương đương với: \(\left\{ \begin{array}{l}x = 2 + z\\y = 2 + 3z\\z - 3\left( {2 + z} \right) - 2\left( {2 + 3z} \right) + z = 0\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}x = 2 + z\\y = 2 + 3z\\ - 8z - 8 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = - 1\\z = - 1\end{array} \right.\)
Vậy hệ phương trình có nghiệm: \(\left( {x;y;z} \right) = \left( {1; - 1; - 1} \right)\).
2) Phương trình tương đương với: \(\left\{ \begin{array}{l}2x - 2 \ge 0\\2{x^2} + 3x - 5 = {\left( {2x - 2} \right)^2}\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}x \ge 1\\2{x^2} + 3x - 5 = 4{x^2} - 8x + 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 1\\2{x^2} - 11x + 9 = 0\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}x \ge 1\\\left( {x - 1} \right)\left( {2x - 9} \right) = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 1\\\left[ \begin{array}{l}x = 1\\x = \frac{9}{2}\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = \frac{9}{2}\end{array} \right.\)
Vậy phương trình có nghiệm: \(x = 1;x = \frac{9}{2}\).
3)
+ Xét \(m - 1 = 0 \Leftrightarrow m = 1\), phương trình trở thành: \( - 6x + 2 = 0 \Leftrightarrow x = \frac{1}{3}\)
Do đó \(m = 1\) thỏa mãn.
+ Xét \(m - 1 \ne 0 \Leftrightarrow m \ne 1\) (*).
Để phương trình có nghiệm duy nhất thì \(\Delta ' = 0\)
\( \Leftrightarrow {\left[ { - \left( {m + 2} \right)} \right]^2} - \left( {m - 1} \right)\left( {m + 1} \right) = 0 \Leftrightarrow {\left( {m + 2} \right)^2} - \left( {{m^2} - 1} \right) = 0\)
\( \Leftrightarrow 4m + 5 = 0 \Leftrightarrow m = - \frac{5}{4}\) (thỏa mãn điều kiện (*))
Kết luận: \(m = 1\) hoặc \(m = - \frac{5}{4}\).
Câu 4:
Từ một điểm A nằm ngoài đường tròn \(\left( {O:R} \right)\) ta vẽ hai tiếp tuyến AB, AC với đường tròn (B,C là tiếp điểm). Trên cung nhỏ BC lấy một điểm M, vẽ \(MI \bot AB,\,\,MK \bot AC\) \(\left( {I \in AB,\,\,K \in AC} \right)\)
1) Chứng minh: AIMK là tứ giác nội tiếp đường tròn.
2) Vẽ \(MP \bot BC\) \(\left( {P \in BC} \right)\). Chứng minh: \(\widehat {MPK} = \widehat {MBC}\).
3) Xác định vị trí của điểm M trên cung nhỏ BC để tích \[MI.MK.MP\] đạt giá trị lớn nhất.
 Xem đáp án
Xem đáp án
1) Ta có \(\widehat {AIM} = \widehat {AKM} = 90^\circ \left( {gt} \right)\), suy ra tứ giác AIMK nội tiếp đường tròn đường kính AM.
Nhận xét: Bài toán chứng minh tứ giác nội tiếp bằng cách chứng minh hai đỉnh cùng nhìn cạnh đối diện dưới góc \(90^\circ \).
2) Tứ giác CPMK có \(\widehat {MPC} = \widehat {MKC} = 90^\circ \) (gt). Do đó CPMK là tứ giác nội tiếp \( \Rightarrow \widehat {MPK} = \widehat {MCK}\)(1). Vì KC là tiếp tuyến của \(\left( O \right)\) nên ta có: \(\widehat {MCK} = \widehat {MBC}\) (cùng chắn ) (2).
Từ (l), (2) \( \Rightarrow \widehat {MPK} = \widehat {MBC}\) (3).
Nhận xét: Bài toán chứng minh hai góc bằng nhau bằng cách sử dụng tính chất bắc cầu.
3) Chứng minh tương tự câu b ta có BPMI là tứ giác nội tiếp.
Suy ra: \(\widehat {MIP} = \widehat {MBP}\) (4). Từ (3) (4) \( \Rightarrow \widehat {MPK} = \widehat {MIP}\)
Tương tự ta chứng minh được \(\widehat {MKP} = \widehat {MPI}\).
Suy ra: \(\Delta MPK\) đồng dạng với \(\Delta MIP\)
\( \Rightarrow \frac{{MP}}{{MK}} = \frac{{MI}}{{MP}} \Rightarrow MI.MK = M{P^2} \Rightarrow MI.MK.MP = M{P^3}\)
Do đó \(MI.MK.MP\) lớn nhất khi và chỉ khi MP lớn nhất.
Gọi H là hình chiếu của O trên BC, suy ra OH là hằng số (do BC cố định).
Lại có: \(MP + OH \le OM = R \Rightarrow MP \le R - OH\). Do đó MP lớn nhất bằng \(R - OH\) khi và chỉ khi \(O,H,M\) thẳng hàng hay M nằm chính giữa cung nhỏ BC.
Suy ra \(max\,MI.MK.MP = {\left( {R - OH} \right)^3} \Leftrightarrow M\) nằm chính giữa cung nhỏ BC.
Câu 5:
Tìm \[a;{\rm{ }}b;{\rm{ }}c\] biết rằng phương trình: \({x^3} + a{x^2} + bx + c = 0\) có tập nghiệm là \(S = \left\{ { - 1;1} \right\}\)?
 Xem đáp án
Xem đáp án
Phương trình có hai nghiệm là \(x = - 1\) và \(x = 1\), thay vào phương trình ta được hệ
\(\left\{ \begin{array}{l} - 1 + a - b + c = 0\\1 + a + b + c = 0\end{array} \right.\)
Trừ hai phương trình trên, ta được: \( - 2 - 2b = 0 \Leftrightarrow b = - 1\)
Cộng hai phương trình trên, ta được: \(a + c = 0 \Leftrightarrow c = - a\)
Phương trình trở thành: \[{x^3} + a{x^2} - x - a = 0\]
\( \Leftrightarrow {x^2}\left( {x + a} \right) - \left( {x + a} \right) \Leftrightarrow \left( {x + a} \right)\left( {{x^2} - 1} \right) = 0\)
Theo giải thiết, phương trình có tập nghiệm là \(S = \left\{ { - 1;1} \right\}\), khi đó phương trình \(x + a = 0\) phải có nghiệm là \( - 1\) hoặc 1, suy ra. \(a = 1\) hoặc \(a = - 1\).
Vậy các số a; b; c cần tìm là \(a = 1;b = - 1;c = - 1\) hoặc \(a = - 1;b = - 1;c = 1\).
