1 câu hỏi trắc nghiệm thuộc Dạng 6: Hệ thức trong hình học có đáp án

Trắc nghiệm Chuyên đề toán 9 Chuyên đề 10: Rèn luyện kĩ năng tìm lời giải bài toán hình học có đáp án

Dạng 6: Hệ thức trong hình học có đáp án

1246 lượt thi
1 câu hỏi
45 phút

Danh sách câu hỏi

Câu 1:

Trên cung BC của đường tròn ngoại tiếp tam giác đều ABC lấy một điểm P tuỳ ý. Các đoạn thẳng AP và BC cắt nhau tại điểm Q. Chứng minh rằng:

\frac{1}{P Q} = \frac{1}{P B} - \frac{1}{P C}

Xem đáp án

Cách giải 1: (Hình 1)

Trên cung BC của đường tròn ngoại tiếp tam giác đều ABC lấy một điểm P tuỳ ý. Các đoạn thẳng AP và BC cắt nhau tại điểm Q (ảnh 1)

Trên đoạn AP lấy hai điểm N và M sao cho BN = BP và PM = PC

Khi đó ta có các tam giác BNP và tam giác MPC là các tam giác cân

Vì

\hat{A P B} = \hat{A C B} = 60^{\circ}

và

\hat{M P C} = \hat{A B C} = 60^{\circ}

(Các góc nội tiếp cùng chắn một cung). Suy ra tam giác BNP và tam giác MPC là các tam giác đều

Xét hai tam giác

△

CQP và

△

BQN có:

\hat{B Q N} = \hat{C Q P}

(Hai góc đổi đỉnh)

\hat{B N Q} = \hat{C P Q} = 60^{\circ}

Nên

△ C Q P ~ △ B Q N \Rightarrow \frac{C P}{P Q} = \frac{B N}{N Q} = \frac{B N}{B N - P Q} \Rightarrow \frac{1}{C P} = \frac{B N - P Q}{P Q . B N}

\frac{1}{P Q} = \frac{1}{P B} - \frac{1}{P C}

(Đpcm)

Cách giải 2: (Hình 2)

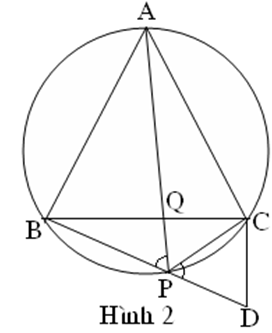
Trên cung BC của đường tròn ngoại tiếp tam giác đều ABC lấy một điểm P tuỳ ý. Các đoạn thẳng AP và BC cắt nhau tại điểm Q (ảnh 2)

Trên tia BP lấy một điểm D sao cho PD = PC
Ta có: $\hat{C P D} = 60^{\circ}$ ( Vì $\hat{C P B} = 120^{\circ}$ góc nội tiếp chắn cung $120^{\circ}$ )
nên tam giác CPD là tam giác đều $\Rightarrow \hat{A P B} = \hat{C D P} = 60^{\circ}$
Vì vậy AP // CD $\Rightarrow △$ BPQ $~ △$ BDC.

$\Rightarrow \frac{B P}{P Q} = \frac{B D}{C D} = \frac{B P + P C}{C P} \Rightarrow \frac{1}{P Q} = \frac{B P + P C}{C P . B P} \Rightarrow \frac{1}{P Q} = \frac{1}{B P} + \frac{1}{C P}$
=> $\frac{1}{P Q} = \frac{1}{P B} - \frac{1}{P C}$ (Đpcm)

Bắt đầu thi ngay

CHỌN BỘ SÁCH BẠN MUỐN XEM

Trắc nghiệm Chuyên đề toán 9 Chuyên đề 10: Rèn luyện kĩ năng tìm lời giải bài toán hình học có đáp án

Dạng 6: Hệ thức trong hình học có đáp án

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương